Hier findest du die Lösungen zu Statistik-Aufgaben, darin geht es um Mittelwert, Median, Quartilsabstand, Boxplot, Stängel-Blatt-Diagramm und klassierte Häufigkeitstabelle.
1. Notenspiegel
Ausführliche Lösungen:
a) Notendurchschnitt
Wir haben hier eine Tabelle, in der steht, dass z. B. 4 Schüler eine 1 haben. Das nennt sich Häufigkeitstabelle. Deshalb müssen wir erst jede Note mit der Anzahl der Schüler mit dieser Note multiplizieren. Danach summiert man alle Werte und dividiert durch die Anzahl aller Schüler.
Notendurchschnitt = \dfrac{4 \cdot 1 + 8 \cdot 1,5 + 10 \cdot 2 + 12 \cdot 2,5 + 15 \cdot 3 + 4 \cdot 3,5 + 3 \cdot 4 + 2 \cdot 4,5 + 2 \cdot 5}{60} = \underline{\underline{2,6}}
Dazu kannst du dir dieses 📽️Video Mittelwert Datenreihe Häufigkeitstabelle ansehen.
b) Klasseneinteilung/absolute Häufigkeit:
Wir haben 9 unterschiedliche Noten und sollen sie in 5 Klassen zusammenfassen. Also müssen wir uns entscheiden, welche wir zusammen fassen. Eine Note muss folglich alleine stehen bleiben. Es ist also auch eine andere Lösung möglich.
| Klasse | 1 \le x \le 2 | 2 \le x < 3 | 3 \le x < 4 | 4 \le x < 5 | 5 \le x \le 6 |
| abs. \, Häufigkeit | 12 | 22 | 19 | 5 | 2 |
Säulendiagramm:
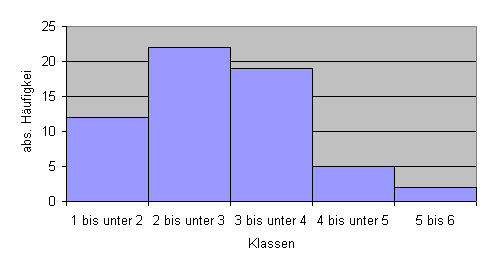
c) Klasseneinteilung/relative Häufigkeit:
| Klasse | 1 \le x \le 2 | 2 \le x < 3 | 3 \le x < 4 | 4 \le x < 5 | 5 \le x \le 6 |
| abs. \, Häufigkeit | 12 | 22 | 19 | 5 | 2 |
| rel. \, Häufigkeit | 20\% | 36,7\% | 31,7\% | 8,3\% | 3,3\% |
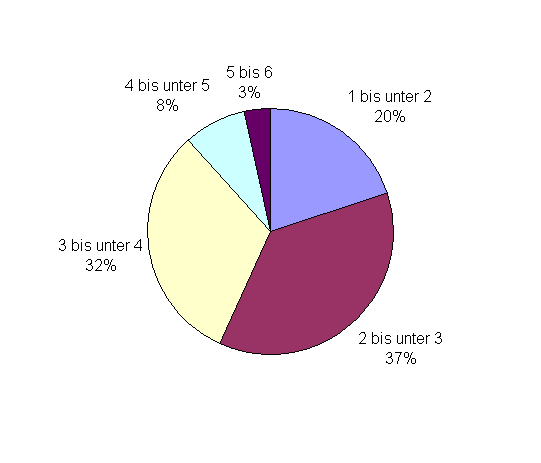
2. Monatseinkommen
Ausführliche Lösung:
Bevor die Vorarbeiterin eingestellt worden ist, sahen die Daten so aus:
325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 €. Der Mittelwert beträgt dabei natürlich ebenfalls 325 €.
Danach sahen die Daten so aus:
325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 325 € | 2800 €.
Der Modus ist der Wert, der am häufigsten vorkommt, das sind die 325 € mit der absoluten Häufigkeit 10. Er bleibt unverändert.
Der Median ist derjenige Wert, der in der Mitte steht, wenn alle Beobachtungswerte der Größe nach geordnet sind. Auch der Median bleibt unverändert. Die 2800 € liegen weit außerhalb der Mitte.
Der Mittelwert ändert sich von 325 € auf \dfrac{3250 € + 2800 €}{11} = \underline{\underline{550 €}}
3. Studierende
Ausführliche Lösungen:
a) Median und Modus
Arithmetisches Mittel:
\overline{x} = \dfrac{1}{n} \sum_{i=1}^n x_i = \dfrac{\sum_{i=1}^n x_i}{n}
mit n = 13 gilt:
\overline{x} = \dfrac{1300 + 1200 + 1400 + 700 + 200 + 750 + 1450 + 1500 + 800 + 800+ 950 + 900 + 3000}{13} \newline = \dfrac{14950}{13} = 1150Die durchschnittlichen Ausgaben betragen \underline{\underline{\overline{x} = 1150 € }}
Median: Wir sortieren die Daten der Größe nach:
| x_1 | x_2 | x_3 | x_4 | x_5 | x_6 | \color{Red}x_7 | x_8 | x_9 | x_{10} | x_{11} | x_{12} | x_{13} |
| 200 | 700 | 750 | 800 | 800 | 900 | \color{Red}950 | 1200 | 1300 | 1400 | 1450 | 1500 | 3000 |
Wenn man den Median finden will, addiert man 1 zu der Anzahl der Daten und teilt dies durch 2.
n = 13 ist ungerade \Rightarrow x_{Med} = x_{frac{n+1}{2}} = x_7 = 950
Der Median bildet das Zentrum der geordneten Daten (Ausgaben) \underline{\underline{x_{Med} = 950 € }}
Der Modus ist der Wert mit der größten Häufigkeit: \underline{\underline{x_{Mod} = 800 €}} \, (Häufigkeit = 2)
b) Die Lagemaße unterscheiden sich voneinander, weil die Ausgaben ungleich verteilt sind (Ausreißer 3000 €).
c) Der Median charakterisiert die Stichprobe am besten, da er gegen Ausreißer unempfindlich ist.
4. Benzinverbrauch
Ausführliche Lösungen:
a) Stängel-Blatt-Diagramm
Beim Stängel-Blatt-Diagramm ordnet man zuerst nach den Stängeln (Zehnerzahlen). Danach schreibt man die Blätter (Einerzahlen) der Größe nach hin.
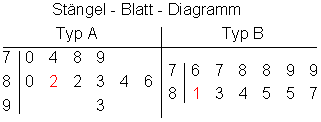
b) Median
Typ A:
Die Anzahl n beträgt hier 11, ist also ungerade. Deshalb berechnen wir den Median, indem wir 1 addieren und durch 2 teilen. Der Median liegt also auf dem 6. Wert und das ist 8,2.
x_{Med} = x_6 = 8,2
Typ B:
Die Anzahl n beträgt hier 12, ist also gerade. Deshalb berechnen wir den Median, indem wir durch 2 teilen. Danach adieren wir diesen Wert und den danach und teilen durch 2. Der Median liegt also zwischen dem 6. und 7. Wert und das ist 8.
x_{Med} = \dfrac{x_6 + x_7}{2} = \dfrac{7,9 + 8,1}{2} = 8
Der Median vom Typ A liegt höher.
c) Mittelwerte
Typ A:
\overline{x_A} = \frac{7,0 + 7,4 + 7,8 + 7,9 + 8,0 + 16,4 + 8,3 + 8,4 + 8,6 + 9,3}{11} = \dfrac{89,1}{11} = \underline{\underline{8,1}}
Typ B:
\overline{x_B} = \frac{7,6 + 7,7 + 15,6 + 15,8 + 8,1 + 8,3 + 8,4 + 17 + 8,7}{} = \dfrac{97,2}{12} = \underline{\underline{8,1}}
Wir sehen also: Typ A und Typ B haben den gleichen Mittelwert: \underline{\underline{\overline{x} = \dfrac{8,1 \, Liter}{100 \, km}}}
d) Mittlere Abweichung
Typ A
| Verbrauch | Mittelwert | Abweichung |
| 7,0 | 8,1 | 1,1 |
| 7,4 | 8,1 | 0,7 |
| 7,8 | 8,1 | 0,3 |
| 7,9 | 8,1 | 0,2 |
| 8,0 | 8,1 | 0,1 |
| 8,2 | 8,1 | 0,1 |
| 8,2 | 8,1 | 0,1 |
| 8,3 | 8,1 | 0,2 |
| 8,4 | 8,1 | 0,3 |
| 8,6 | 8,1 | 0,5 |
| 9,3 | 8,1 | 1,2 |
| Summe der Abweichungen | xx | |
| Mittlere Abweichung: 4,8:11 | 0,44 | |
Typ B
| Verbrauch | Mittelwert | Abweichung |
| 7,6 | 8,1 | 0,5 |
| 7,7 | 8,1 | 0,4 |
| 7,8 | 8,1 | 0,3 |
| 7,8 | 8,1 | 0,3 |
| 7,9 | 8,1 | 0,2 |
| 7,9 | 8,1 | 0,2 |
| 8,1 | 8,1 | 0,0 |
| 8,3 | 8,1 | 0,2 |
| 8,4 | 8,1 | 0,3 |
| 8,5 | 8,1 | 0,4 |
| 8,5 | 8,1 | 0,4 |
| 8,7 | 8,1 | 0,6 |
| Summe der Abweichungen | xx | |
| Mittlere Abweichung: 3,8:12 | 0,32 | |
Die mittlere Abweichung bei Typ A ist höher.
Die Werte bei Typ B scharen sich mehr um den Mittelwert.
5. Berechne Mittelwert, Median und QuartilsabstandAusführliche Lösung:
Mittelwert:
\overline{x} = \dfrac{1}{n} \sum_{i=1}^n x_i \, mit n = 11 \, gilt:
\overline{x} = \dfrac{1}{11}(3 + 8 + 12 + 5 +7 + 8 + 9,5 + 11 + 14 + 6 + 8,5) = \dfrac{92}{11} = \underline{\underline{8,\overline{36}}} \newline
Die Daten werden nach Größe geordnet:
3 \Big| 5 \Big| {\color{Blue}6} \Big| 7 \Big| 8 \Big| {\color{Red}8} \Big| 8,5 \Big| 9,5 \Big| {\color{Blue}11} \Big| 12 \Big| 14 \newline
Median: {\color{Red}x_{Med}} = x_6 = \underline{\underline{8}}
Quartil 1: {\color{Blue}Q_1} = x_3 = \underline{\underline{6}}
Quartil 3: {\color{Blue}Q_3} = x_9 = \underline{\underline{11}}
Quartilsabstand: Q_A = Q_3 - Q_1 = 11 - 6 = \underline{\underline {65}}
Ca. 50% der Daten liegen zwischen den Werten 6 und 11.
6. Körpergewicht
Ausführliche Lösung:
Spannweite und Median:
männlich:
\begin{matrix} \boldsymbol{6} & 0 & \, & \, 7 & 7 & 8 & 8 & \, \\ \boldsymbol{7} & 0 & 0 & 2 & 3 & 5 & 6 & 8 \\ \boldsymbol{8} & \, & \, & \, 4 & \, & \, & \, \end{matrix}
Spannweite: R = 84-60 = \underline{\underline{24}}
Median: x_{Med} = x_7 = \underline{\underline{70}}
Quartile: Q_1 = \dfrac{x_3 + x_4}{2} = \dfrac{67+68}{2} = \underline{\underline{67,5}} \qquad Q_3 = \dfrac{x_{10}+x{11}}{2} = \dfrac{75+76}{2} = \underline{\underline{75,5}}
Q-Abstand: Q_A = Q_3 - Q_1 = 75,5 - 67.5 = \underline{\underline{8}}
weiblich:
\begin{matrix} \boldsymbol{5} & 1 & 1 & 2 & 4 & 5 & 7 & 8 & 9 \\ \boldsymbol{6} & \, & 0 & 3 & 3 & 3 & 4 & \, & \, \end{matrix}
Spannweite: R = 64 - 51 = \underline{\underline{13}}
Median: x_{Med} = \dfrac{x_7 + x_8}{2} = \dfrac{57 + 58}{2} = \underline{\underline{57,5}}
Quartile: Q_1 = x_4 = \underline{\underline{54}} \qquad Q_3 = x_{11} = \underline{\underline{63}}
Q-Abstand: Q_A = Q_3 - Q_1 = 63 - 54 = \underline{\underline{9}}
Boxplott:
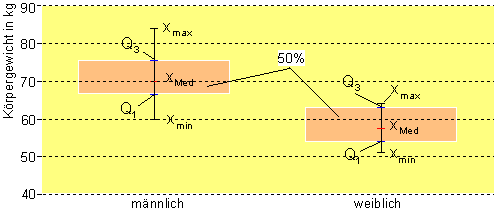
Vergleich der Darstellungen:
Bei den Schülern liegt der Median viel höher als bei den Schülerinnen, sie bringen einfach mehr Gewicht auf die Waage. Der 50%-Bereich ist geringer, dafür ist die Spannweite fast doppelt so groß.
Hier findest du Aufgaben hierzu.
Theorie hierzu: Mittelwert, Median und Modalwert.
und Quartilsabstand.
Alle Formeln zur beschreibenden Statistik sind hier übersichtlich zusammengestellt.
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik, dort auch Links zu weiteren Aufgaben.

