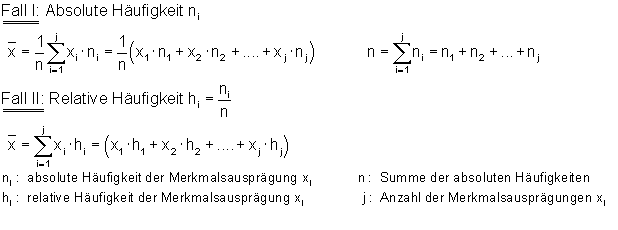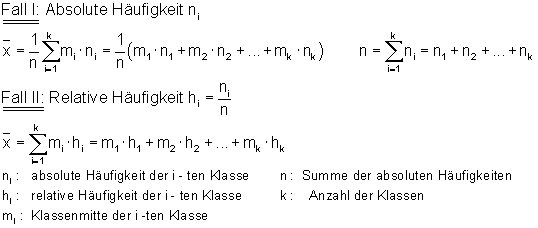Hier findest du eine Statistik Formelsammlung mit Beispielen.
- Das arithmetische Mittel
- Mittelwert
- Median
- Spannweite
- Quartilsabstand
- Varianz und Standardabweichung
- Links zu Aufgaben
Das arithmetische Mittel
Arithmetisches Mittel einer Datenreihe
Das arithmetischen Mittel berechnet man folgendermaßen aus einer Datenreihe:
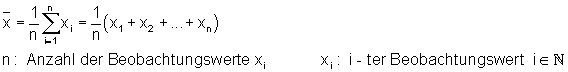
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Arithmetisches Mittel aus einer Häufigkeitstabelle
Das arithmetischen Mittel berechnet man folgendermaßen aus einer Häufigkeitstabelle. Dabei muss man zwischen der absoluten und der relativen Häufigkeit unterscheiden:
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Mittelwert bei klassierten Daten aus einer Häufigkeitstabelle
Den Mittelwert bei klassierten Daten berechnet man folgendermaßen aus einer Häufigkeitstabelle:
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Der Median
Den Median berechnet man folgendermaßen:
Wenn n die Anzahl der Beobachtungswerte x_i ist, dann gilt:
n ungerade \Rightarrow x_{Med} = x_{\frac{n + a}{2}} \\
n gerade \Rightarrow x_{Med} = \frac{1}{2} (x_{\frac{n}{2}} + x_{\frac{n}{2}+1})
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Die Spannweite
Die Spannweite berechnet man folgendermaßen:
Spannweiter = größter Beobachtungswert – kleinster Beobachtungswert
R = x_{max} - x_{min}
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Der Quartilsabstand
Berechnung des Quartilsabstands
Der mittlere 50 %-Bereich aller Beobachtungswerte heißt Quartilabstand. Man berechnet ihn folgendermaßen:
Q_A = Q_3 - Q_1
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Varianz und Standardabweichung
Varianz einer Datenreihe
Die Varianz aus einer Datenreihe berechnet man wie folgt:
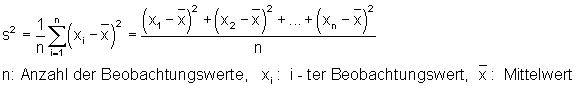
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Die Standardabweichung berechnet man folgendermaßen:
S = \sqrt{s^2} = \sqrt{Varianz}
Berechnung der Varianz einer Häufigkeitstabelle
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Berechnung der Varianz einer klassierten Häufigkeitstabelle
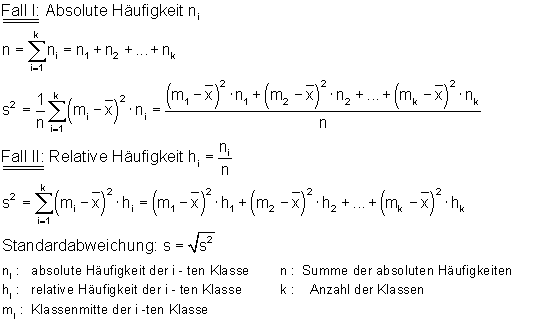
Hier findest du ausführliche Erklärungen zu den Formeln. Außerdem viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Aufgaben hierzu Statistik vermischte Aufgaben.
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik, dort auch Links zu weiteren Aufgaben.
Dazu kannst du auch den Wikipedia-Arikel zur Statistik lesen.