Hier findet ihr die Lösungen der Aufgaben zur Kombinatorik I, auch Zählstrategie genannt. Diesmal geht es um geordnete und ungeordnete Stichproben mit und ohne Zurücklegen. Außerdem um die Wahrscheinlichkeiten beim Lottospielen.
1.
Ein Zufallsgenerator (Codeknacker) erzeugt unabhängig voneinander 4 Ziffern von 0 bis 9. Nach der Generierung werden diese als 4-stellige Zahl auf einem Display angezeigt. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
A: Alle Ziffern sind ungerade.
B: Es kommen nur die Ziffern 0 und 1 vor.
C: Die Zahl ist eine „Spiegelzahl“, d.h. die erste und die letzte sowie die zweite und die dritte Zahl sind gleich.
1. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Geordnete Stichprobe mit Zurücklegen, siehe Kombinatorik.
Die Anzahl aller Möglichkeiten:
Für jede der 4 Stellen gibt es 10 mögliche Ziffern (0 bis 9). Damit lassen sich 10.000 Zahlen darstellen.
A:
Alle Ziffern sind ungerade.
{ 1 ; 3 ; 5 ; 7 ; 9 } Die Anzahl der Möglichkeiten für A ist 54.
![]()
die Wahrscheinlichkeit dafür, dass alle Ziffern ungerade sind.
B:
Nur die Zahlen 0 und 1 kommen vor.
{ 0 ; 1 } Die Anzahl der Möglichkeiten für B ist 24.
![]()
die Wahrscheinlichkeit dafür, dass nur die Ziffern 0 und 1 vorkommen.
C:
Es kommen nur Spiegelzahlen vor. [xy|yx]
Die erste und die zweite Zahl ist frei wählbar, daraus ergeben sich die beiden anderen. Die Anzahl der Möglichkeiten für C ist 102.
![]()
die Wahrscheinlichkeit dafür, dass die angezeigte Zahl eine Spiegelzahl ist. Eine JavaScript-Simulation dazu.
2.
In einer Urne sind 6 rote und 4 weiße Kugeln. Es werden nacheinander 5 Kugeln ohne Zurücklegen gezogen. Wie groß ist die Wahrscheinlichkeit der folgenden Ereignisse?
A: Man zieht nur rote Kugeln.
B: Man zieht zuerst alle weißen, dann eine rote Kugel.
C: Die erste Kugel ist weiß.
D: Man zieht abwechselnd weiße und rote Kugeln.
2. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Geordnete Stichprobe ohne Zurücklegen, siehe Kombinatorik.
6 rote und 4 weiße Kugeln ergibt n = 10 Kugeln. Es wird k = 5 mal gezogen ohne Zurücklegen.
![]()
A:
Nur rote Kugeln werden gezogen.
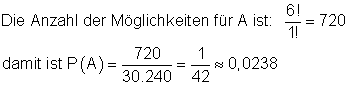
die Wahrscheinlichkeit dafür, dass nur rote Kugeln gezogen werden.
B:
Man zieht zuerst alle weißen, dann eine rote Kugel.
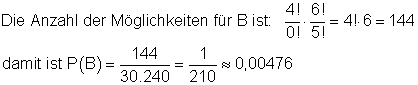
die Wahrscheinlichkeit dafür, zuerst alle weißen und dann eine rote Kugel zu ziehen.
C:
Die erste Kugel ist weiß. (bedeutet, die 2., 3., 4. und 5. Kugel ist beliebig)
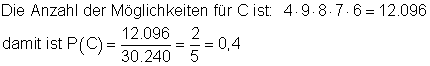
die Wahrscheinlichkeit dafür, im ersten Zug die weiße Kugel zu ziehen.
D:
Man zieht abwechselnd weiß und rot. (wrwrw) oder (rwrwr).

die Wahrscheinlichkeit dafür, abwechselnd weiße und rote Kugeln zu ziehen.
3.
In einer Urne befinden sich 25 nummerierte Kugeln (Zahlen 1 bis 25). Es werden gleichzeitig 4 Kugeln aus der Urne gezogen. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
A: Alle Zahlen sind durch 5 teilbar.
B: Alle Zahlen sind gerade.
C: Die Summe der 4 Zahlen ist kleiner als 12.
D: Das Produkt der 4 Zahlen ist 12.
3. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Ungeordnete Stichprobe ohne Zurücklegen oder Ziehen mit einem Griff, siehe Kombinatorik.
Die durch 5 teilbaren Zahlen sind: 5, 10, 15, 20, 25
Die Anzahl der Möglichkeiten aus 25 unterschiedlichen Kugeln 4 zu ziehen ist:
![]()
Das ist die Anzahl aller Möglichkeiten.
A:
Alle Zahlen sind durch 5 teilbar.
Die Anzahl der durch 5 teilbaren Zahlen ist 5.
Die Anzahl der Möglichkeiten daraus 4 auszuwählen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von A. Damit ist
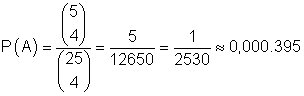
die Wahrscheinlichkeit dafür 4 Zahlen zu ziehen, die durch 5 teilbar sind.
B:
Alle Zahlen sind gerade.
Die geraden Zahlen sind: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24
Die Anzahl der geraden Zahlen ist 12.
Die Anzahl der Möglichkeiten daraus 4 auszuwählen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von B. Damit ist
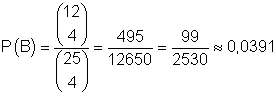
die Wahrscheinlichkeit dafür 4 gerade Zahlen zu ziehen.
C:
Die Summe der 4 Zahlen ist kleiner als 12.
1 + 2 + 3 + 4 = 10 < 12
1 + 2 + 3 + 5 = 11 < 12
Es gibt für das Ereignis C nur 2 Möglichkeiten. Damit ist
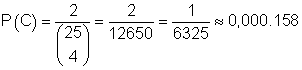
die Wahrscheinlichkeit dafür, 4 Zahlen zu ziehen, deren Summe kleiner als 12 ist.
D:
Das Produkt der 4 Zahlen ist 12.
![]()
ist die Wahrscheinlichkeit dafür, 4 Zahlen zu ziehen, deren Produkt 12 ist.
4.
Vier Freunde gehen ins Kino. Sie haben in einer Reihe 4 nummerierte Plätze nebeneinander und verteilen die Karten zufällig. Wie groß ist die Wahrscheinlichkeit der folgenden Ereignisse?
A: Sven sitzt zwischen zwei Freunden.
B: Sven und Kai sitzen außen.
C: Sven und Kai sitzen nebeneinander.
4. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Anordnung von k Elementen, siehe Kombinatorik.
Die Anzahl der Möglichkeiten 4 Personen auf 4 Plätze zu verteilen ist 4!
A:
Sven sitzt zwischen zwei Freunden.
Er hat zwei Möglichkeiten: xSxx oder xxSx (Platz 2 oder Platz 3)
Die drei Freunde haben 3! Möglichkeiten
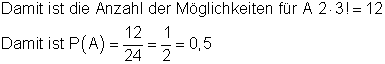
die Wahrscheinlichkeit dafür, dass Sven zwischen zwei Freunden sitzt.
B:
Sven und Kai sitzen außen.
SxxK oder KxxS Sven und Kai haben 2 Möglichkeiten, die beiden Freunde ebenfalls.
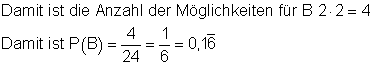
die Wahrscheinlichkeit dafür, dass Sven und Kai außen sitzen.
C:
Sven und Kai sitzen nebeneinander.
SKxx KSxx xSKx xKSx xxSK xxKS das sind 6 Möglichkeiten.
Für die beiden anderen gibt es 2 Möglichkeiten.
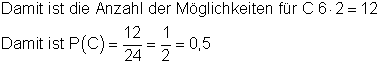
die Wahrscheinlichkeit dafür, dass Sven und Kai nebeneinander sitzen.
5.
Bestimmen Sie die Wahrscheinlichkeit für 6, 5, 4, 3 Richtige im Lotto 6 aus 49 und beschreiben Sie dabei Ihre Vorgehensweise.
A: 6 Richtige im Lotto
B: 5 Richtige im Lotto
C: 4 Richtige im Lotto
D: 3 Richtige im Lotto
5. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Ungeordnete Stichprobe ohne Zurücklegen oder Ziehen mit einem Griff, siehe Kombinatorik.
Die Anzahl der Möglichkeiten 6 Zahlen von insgesamt 49 Zahlen zu anzukreuzen ist:
![]()
A:
6 Richtige im Lotto:
Die Anzahl der Möglichkeiten 6 Zahlen von insgesamt 6 Gewinnzahlen anzukreuzen und 0 Zahlen von 43 Nicht- Gewinnzahlen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von A.
Damit ist

die Wahrscheinlichkeit dafür, dass 6 Gewinnzahlen angekreuzt wurden (6 richtige).
B:
5 Richtige im Lotto:
Die Anzahl der Möglichkeiten 5 Zahlen von insgesamt 6 Gewinnzahlen anzukreuzen und 1 Zahl von 43 Nicht- Gewinnzahlen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von B.
Damit ist
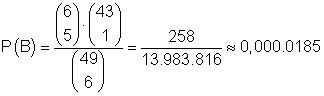
die Wahrscheinlichkeit dafür, dass 5 Gewinnzahlen angekreuzt wurden (5 richtige).
C:
4 Richtige im Lotto:
Die Anzahl der Möglichkeiten 4 Zahlen von insgesamt 6 Gewinnzahlen anzukreuzen und 2 Zahl von 43 Nicht- Gewinnzahlen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von C.
Damit ist
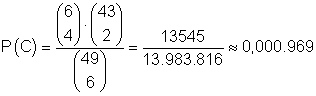
die Wahrscheinlichkeit dafür, dass 4 Gewinnzahlen angekreuzt wurden (4 richtige).
D:
3 Richtige im Lotto:
Die Anzahl der Möglichkeiten 3 Zahlen von insgesamt 6 Gewinnzahlen anzukreuzen und 3 Zahl von 43 Nicht- Gewinnzahlen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von D.
Damit ist
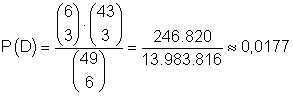
die Wahrscheinlichkeit dafür, dass 3 Gewinnzahlen angekreuzt wurden (3 richtige).
6.
Zum Auffädeln einer Kette stehen rote, blaue und grüne Perlen zur Verfügung. Es werden 6 Perlen aufgefädelt. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse, wenn die Farben zufällig gewählt werden?
A: Es kommt keine rote Perle vor.
B: Die ersten 3 Perlen sind grün.
C: Es kommen immer abwechselnd nur rote und grüne Perlen vor.
6. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Geordnete Stichprobe mit Zurücklegen, siehe Kombinatorik
Die Farbauswahl ist zufällig, das bedeutet, jede Farbe ist gleichwahrscheinlich.
Für jede Perle stehen 3 Farben zur Verfügung.
Damit ist die Anzahl aller Möglichkeiten 36 = 729
A:
Es kommt keine rote Perle vor.
Die Anzahl der Möglichkeiten nur zwei Farben zu ziehen ist 26 = 64
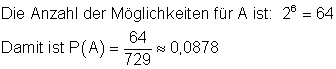
die Wahrscheinlichkeit dafür, dass keine Perle rot ist.
B:
Die ersten drei Perlen sind grün.
Damit können die letzten 3 beliebig gewählt werden.
Also eine Möglichkeit für ggg und 33 Möglichkeiten für die anderen drei.

die Wahrscheinlichkeit dafür, dass die ersten drei Perlen grün sind.
C:
Die Perlen sind abwechselnd rot und grün.
Dafür gibt es zwei Möglichkeiten: rgrgrg oder grgrgr
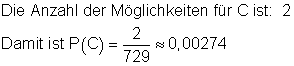
die Wahrscheinlichkeit dafür, dass die Perlen abwechselnd rot und grün sind.
7.
Auf einer Geburtstagsfeier werden unter 10 Mädchen ein 1., ein 2. und ein 3. Preis verlost. Wie groß ist die Wahrscheinlichkeit der folgenden Ereignisse?
A: Anja gewinnt den 1., Inge den 2. und Karin den 3. Preis.
B: Anja, Inge und Karin gewinnen je einen Preis.
C: Anja gewinnt keinen Preis.
D:Keines der drei Mädchen Anja, Inge und Karin gewinnt einen Preis.
7. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Geordnete Stichprobe ohne Zurücklegen, siehe Kombinatorik
![]()
A:
Anja (1. Preis). Inge (2. Preis). Karin (3. Preis).
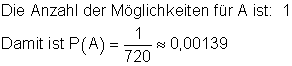
die Wahrscheinlichkeit dafür, dass Anja den 1.Preis, Inge den 2. Preis und Karin den 3. Preis bekommt.
B:
Anja, Inge und Karin gewinnen je einen Preis.
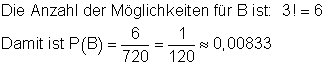
die Wahrscheinlichkeit dafür, dass Anja , Inge und Karin je einen Preis gewinnen.
C:
Anja gewinnt keinen Preis.
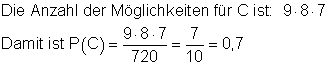
die Wahrscheinlichkeit dafür, dass Anja keinen Preis gewinnt.
D:
Keines der drei Mädchen gewinnt einen Preis.
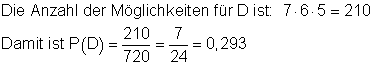
die Wahrscheinlichkeit dafür, dass keins der drei Mädchen einen Preis gewinnt.
8.
In einem Kurs mit 12 Jungen und 13 Mädchen werden 5 Freikarten verlost. Dazu werden die Namen der 25 Schüler/innen auf Zettel geschrieben und 5 Zettel zufällig herausgegriffen. Mit welcher Wahrscheinlichkeit fallen 5 , (4, 3, 2, 1, 0) Freikarten an die Mädchen (Jungen)?
A: Die Mädchen bekommen 5 Freikarten.
B: Die Mädchen bekommen 4 Freikarten.
C: Die Mädchen bekommen 3 Freikarten.
D: Die Mädchen bekommen 2 Freikarten.
E: Die Mädchen bekommen 1 Freikarte.
F: Die Mädchen bekommen keine Freikarte.
8. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Ungeordnete Stichprobe ohne Zurücklegen oder Ziehen mit einem Griff, siehe Kombinatorik
Die Anzahl der Möglichkeiten 5 Zettel aus insgesamt 25 Zetteln zu ziehen ist:
![]()
A:
5 Zettel gehen an die Mädchen (0 Zettel an die Jungen)
Die Anzahl der Möglichkeiten 5 Zettel aus insgesamt 13 Zetteln mit Mädchennamen zu ziehen und 0 Zettel aus insgesamt 12 Zetteln mit Jungsnamen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von A.
Damit ist
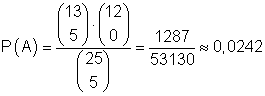
die Wahrscheinlichkeit dafür, dass alle 5 Freikarten an die Mädchen gehen.
B:
4 Zettel gehen an die Mädchen (1 Zettel an die Jungen)
Die Anzahl der Möglichkeiten 4 Zettel aus insgesamt 13 Zetteln mit Mädchennamen zu ziehen und 1 Zettel aus insgesamt 12 Zetteln mit Jungennamen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von B.
Damit ist
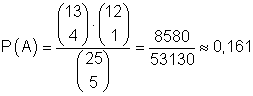
die Wahrscheinlichkeit dafür, dass 4 Freikarten an die Mädchen und 1 Freikarte an die Jungen gehen.
C:
3 Zettel gehen an die Mädchen (2 Zettel an die Jungen)
Die Anzahl der Möglichkeiten 3 Zettel aus insgesamt 13 Zetteln mit Mädchennamen zu ziehen und 2 Zettel aus insgesamt 12 Zetteln mit Jungsnamen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von C.
Damit ist
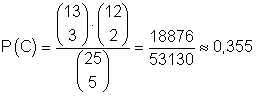
die Wahrscheinlichkeit dafür, dass 3 Freikarten an die Mädchen und 2 Freikarte an die Jungen gehen.
D:
2 Zettel gehen an die Mädchen (3 Zettel an die Jungen)
Die Anzahl der Möglichkeiten 2 Zettel aus insgesamt 13 Zetteln mit Mädchennamen zu ziehen und 3 Zettel aus insgesamt 12 Zetteln mit Jungsnamen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von D.
Damit ist
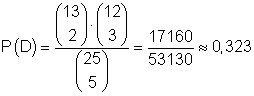
die Wahrscheinlichkeit dafür, dass 2 Freikarten an die Mädchen und 3 Freikarte an die Jungen gehen.
E:
1 Zettel geht an die Mädchen (4 Zettel an die Jungen)
Die Anzahl der Möglichkeiten 1 Zettel aus insgesamt 13 Zetteln mit Mädchennamen zu ziehen und 4 Zettel aus insgesamt 12 Zetteln mit Jungsnamen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von E.
Damit ist
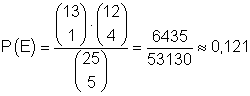
die Wahrscheinlichkeit dafür, dass 1 Freikarte an die Mädchen und 4 Freikarte an die Jungen gehen.
F:
0 Zettel gehen an die Mädchen (5 Zettel an die Jungen)
Die Anzahl der Möglichkeiten 0 Zettel aus insgesamt 13 Zetteln mit Mädchennamen zu ziehen und 5 Zettel aus insgesamt 12 Zetteln mit Jungsnamen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von F.
Damit ist
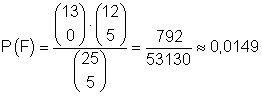
die Wahrscheinlichkeit dafür, dass 0 Freikarten an die Mädchen und 5 Freikarte an die Jungen gehen.
9.
Für eine Prüfung werden 10 mögliche Themen vereinbart. Drei davon werden in der Prüfung abgefragt. Ein Prüfling lernt nur 6 der 10 Themen. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
A: Der Prüfling hat keins der drei ausgewählten Themen vorbereitet.
B: Der Prüfling hat eins der drei ausgewählten Themen vorbereitet.
C: Der Prüfling hat zwei der drei ausgewählten Themen vorbereitet.
D: Der Prüfling hat sich auf alle drei ausgewählten Themen vorbereitet
9. Ausführliche Lösungen
Hierbei brauchen wir das Modell: Ungeordnete Stichprobe ohne Zurücklegen oder Ziehen mit einem Griff, siehe Kombinatorik
10 mögliche Themen, 3 werden abgefragt, Prüfling lernt für 6.Anzahl der Möglichkeiten aus 10 Themen 3 auszuwählen ist:
![]()
A:
Der Prüfling hat sich auf keins der drei ausgewählten Themen vorbereitet.
Aus den 4 Themen, auf die der Prüfling sich nicht vorbereitet hat, werden 3 ausgewählt.
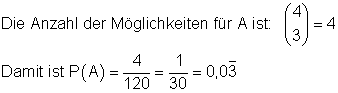
die Wahrscheinlichkeit dafür, dass der Prüfling sich auf kein Thema vorbereitet hat.
B:
Der Prüfling hat sich auf eins der drei ausgewählten Themen vorbereitet.
Aus den 4 Themen, auf die der Prüfling sich nicht vorbereitet hat, werden 2 ausgewählt, aus den 6 Themen auf die er sich vorbereitet hat wird 1 Thema ausgewählt.

die Wahrscheinlichkeit dafür, dass der Prüfling sich auf ein Thema vorbereitet hat.
C:
Der Prüfling hat sich auf zwei der drei ausgewählten Themen vorbereitet.
Aus den 4 Themen, auf die der Prüfling sich nicht vorbereitet hat, wird 1 ausgewählt, aus den 6 Themen auf die er sich vorbereitet hat werden 2 Thema ausgewählt.

die Wahrscheinlichkeit dafür, dass der Prüfling sich auf zwei Themen vorbereitet hat.
D:
Der Prüfling hat sich auf alle drei der drei ausgewählten Themen vorbereitet.
Aus den 4 Themen, auf die der Prüfling sich nicht vorbereitet hat, wird 0 ausgewählt, aus den 6 Themen auf die er sich vorbereitet hat werden 3 Thema ausgewählt.

die Wahrscheinlichkeit dafür, dass der Prüfling sich auf alle 3 Themen vorbereitet hat.
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

