Lösungen Hypothesentest I Casio fx-CG50• 123mathe

Hier findet ihr die Lösungen zum Hypothesentest I mit dem grafikfähigen Taschenrechner Casio fx-CG50 und Casio fx-CG20. Abweichungen der Ergebnissen sind entstanden, weil ich die Originalaufgaben mit Tabellenwerten entsprechender Binomialverteilungen, bzw. mit Näherungswerten der Normalverteilung berechnet habe.

Hier findest du eine Einführung in den Casio fx-CG20 und Casio fx-CG 50.

Update auf Casio fx-CG50

Wer noch den Casio fx-CG20 hat, kann sich auf der Webseite der Firma ein kostenloses Update herunterladen. Dann kannst du auch die neuen Funktionen des Casio fx-CG50 nutzen. Suche dazu auf der Seite von Casio nach ‚FX-CG20 & FX-CG50 Betriebssystem-Update‘. Ich gebe hier jedoch nicht den direkten Link ein, weil es in der Zwischenzeit vielleicht bereits ein neueres Update gibt.

Aufgabe 1. Ausführliche Lösung

Nullhypothese: H₀: p ≤ 0,1 Alternativhypothese: H₁: p > 0,1
Signifikanzniveau: α ≤ 5%.
Bei einem Erhebungsumfang von n = 200 verzeichnet man k Erfolge.
Es handelt sich um einen rechtseitigen Hypothesentest, denn große Werte von k sprechen gegen H₀.

Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

Bei einer Anzahl von k = 28 oder mehr Erfolgen, würde die Nullhypothese abgelehnt und die Alternativhypothese angenommen werden.
Der dabei auftretende Fehler (Fehler 1. Art) wäre dann etwa 4,34%.Eingabeprozedur:

Aufgabe 2. Ausführliche Lösung

Nullhypothese: H₀: p ≤ 0,37 Alternativhypothese: H₁: p > 0,37
Signifikanzniveau: α ≤ 5%.
Bei einem Erhebungsumfang von n = 200 verzeichnet man k Erfolge.
Es handelt sich um einen rechtseitigen Hypothesentest, denn große Werte von k sprechen gegen H₀.

Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

Bei einer Anzahl von k = 86 oder mehr Erfolgen, würde die Nullhypothese abgelehnt und die Alternativhypothese angenommen werden.
Der dabei auftretende Fehler (Fehler 1. Art) wäre dann etwa 4,7%.Eingabeprozedur:

Aufgabe 3.1 Ausführliche Lösung

Nullhypothese: H₀: p = 0,75 Alternativhypothese: H₁: p ≠ 0,75
Signifikanzniveau: α ≤ 5%.
Fehler 2. Art für p = 0,7 ermitteln.
Bei einem Erhebungsumfang von n = 120 verzeichnet man k Erfolge.
Es handelt sich um einen beidseitigen Hypothesentest, denn kleine, wie auch große Werte von k sprechen gegen H₀.
Da es zwei Ablehnungsbereiche gibt, wird hier die Vereinbarung getroffen, dass diese sich symmetrisch zum Erwartungswert 90 positionieren.

Berechnung des Ablehnungsbereichs und Überprüfung des tatsächlichen Signifikanzniveaus.

Der linke Ablehnungsbereich wird aus Symmetriegründen um eins erhöht.
Dadurch ändern sich die Werte, rot in Klammern beschrieben.
Ablehnungs- und Annahmebereich sehen dann wie folgt aus:
{ 0 … 80 } { 81 …. 90 … 99 } { 100 … 120 }Fällt die Anzahl k der Erfolge in einen der beiden Ablehnungsbereiche, wird die Nullhypothese abgelehnt und die Alternativhypothese angenommen.
Der dabei auftretende Fehler (Fehler 1. Art) wäre dann etwa 4,44%.

Eingabeprozedur:

Aufgabe 3.2 Ausführliche Lösung

Falls H₀ nicht gilt, sondern p = 0,7 richtig ist, d.h. die Hypothese p = 0,75 ist falsch, aber das Stichprobenergebnis fällt zufällig in den Annahmebereich von H₀ , nimmt man H₀ fälschlicherweise an.
Die Wahrscheinlichkeit dafür, diesen Fehler zu machen ist der Fehler 2. Art.
Man bestimmt diesen Fehler, indem man unter der Annahme, dass p = 0,7 richtig ist, die Wahrscheinlichkeit des Annahmebereichs von H₀ berechnet.

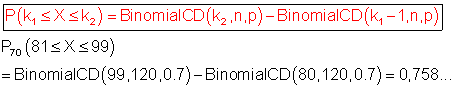
Falls H₀ falsch und p = 0,7 richtig ist, fällt das Ergebnis dennoch zu 75,8% in den Annahmebereich von H₀.
Die Nullhypothese würde fälschlicherweise angenommen werden.
Dieser Fehler heißt Fehler 2. Art.
Er beträgt 75,8% und ist im Vergleich zum Fehler 1. Art mit 4,44% sehr groß.

Eingabeprozedur: