Hier findest du Aufgaben und Lösungen zur Tangente. Zuerst gebe ich noch ein paar Erklärungen und Tipps zum Vorgehen.
Überblick:
Mit Klick auf einen der Punkte gelangst du sofort dorthin.
1. Tipps zum Lösen der Aufgaben zur Tangente:
Um die Aufgaben zur Tangente zu verstehen, ist folgendes wichtig:
Die Steigung des Graphen einer Funktion f(x) in einem Punkt P(x0|y0), ist gleich der Steigung mt der Tangente t(x) in diesem Punkt. Außerdem ist diese Steigung gleich der ersten Ableitung in diesem Punkt f'(x0).
Also: Steigung von f(x) in P(x0|y0)
= Steigung mt der Tangente t(x) in P(x0|y0)
= f'(x0) also Ableitung im Punkt P(x0|y0).
Um die Aufgaben zur Tangente zu lösen, errechnet man also y0 indem man x0 in f(x) einsetzt. Damit haben wir die Koordinaten von P(x0|y0).
Dann leitet man f'(x) ab und berechnet den f'(x0).
Für die Tangentengleichung t(x) = mtx + bt brauchen wir noch bt. Dazu gibt es zwei Möglichkeiten:
a) Wir setzen die Werte des Punktes P(x0|y0) ein (Siehe auch Berechnung der Funktionsgleichung einer Geraden Fall I):
b) Einfacher ist es, wenn wir die erste Ableitung verwenden (Siehe Herleitung der Tangentengleichung):
t(x) = f'(x) \cdot (x - x_0) + f(x_0)
In den Lösungen habe ich diese zweite Methode benutzt.
Dazu kannst du dir das 📽️ Video Tangente im Punkt P berechnen ansehen.
2. Aufgaben zur Tangente:
1. f(x)= x^3-6x^2+9x \quad x_0 =2
2. f(x)=\dfrac{1}{4}x^3+\dfrac{15}{4}x^2+\dfrac{9}{4} \quad x_0 =2
3. f(x) = \dfrac{1}{2}x^3 - \dfrac{1}{2}x^2-4x + 4 \quad x_0=-1
4. f(x)= x^3+3x^2-2 \quad x_0=1
5. f(x)=\dfrac{1}{2}x^3 - \dfrac{1}{2}x^2-\dfrac{5}{2}x + 3 \quad x_0=1
6. f(x)=x^3 - x^2 - 5x -2 \quad x_0=-\dfrac{3}{2}
7. f(x)=\dfrac{1}{4}x^3-\dfrac{5}{4}x^2+\dfrac{1}{2}x+2 \quad x_0=3
8. f(x)=x^3-\dfrac{3}{2}x^2-6x+2 \quad x_0=1
9. f(x)=\dfrac{1}{2}x^3 - \dfrac{1}{2}x^2 - 4x + 4 \quad x_0=0
10. f(x)= \dfrac{1}{3}x^3 - \dfrac{1}{3}x^2-4x+4 \quad x_0=1
3. Lösungen
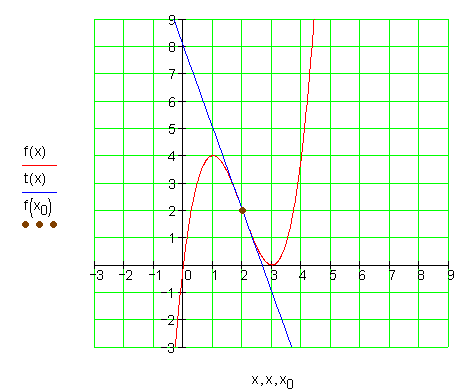
1.
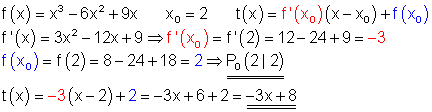
Die Graphen:![]()
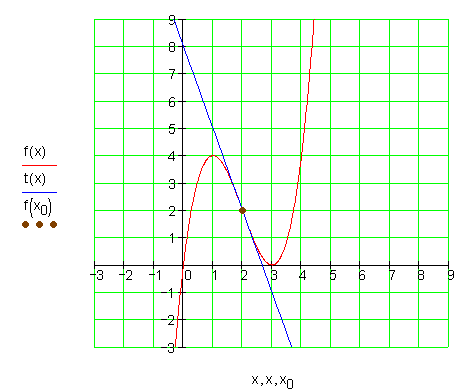
2.
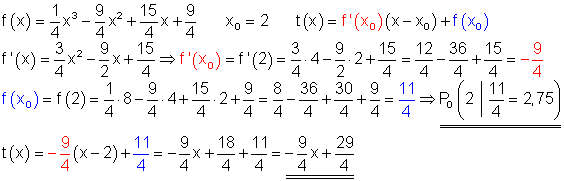
Die Graphen:
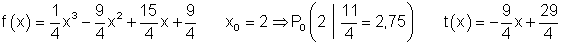
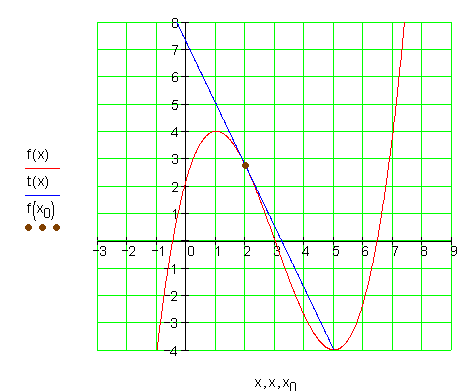
3.
Berechnung: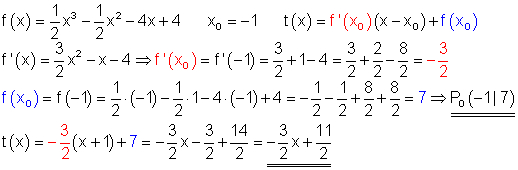
Die Graphen:![]()
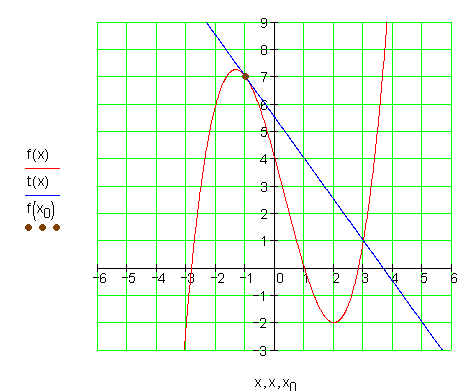
4.
Berechnung: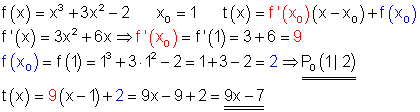
Die Graphen:![]()
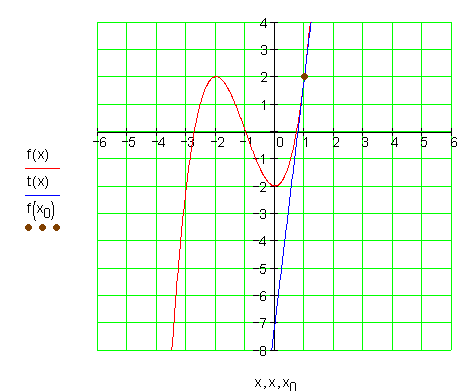
5.
Berechnung: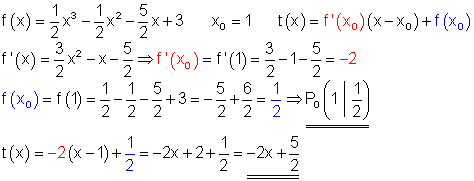
Die Graphen:![]()
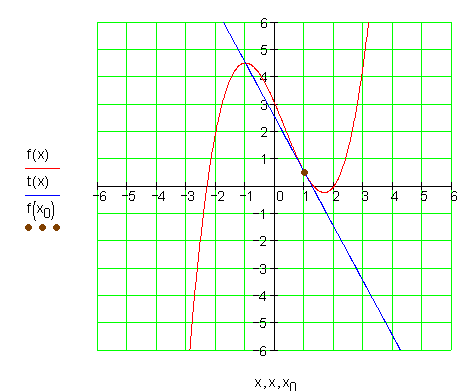
6.
Berechnung: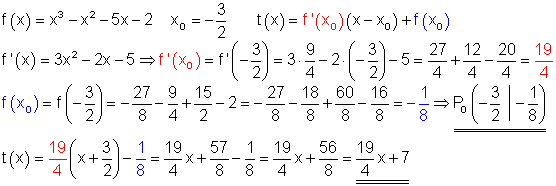
Die Graphen:![]()
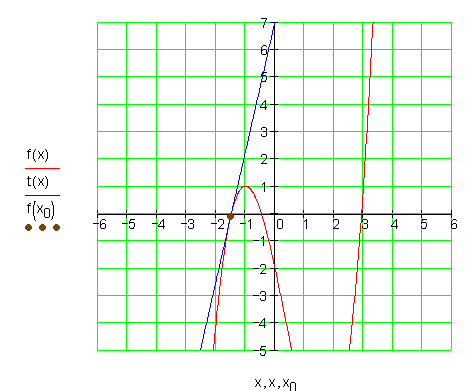
7.
Berechnung: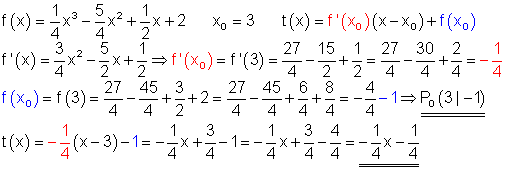
Die Graphen:![]()
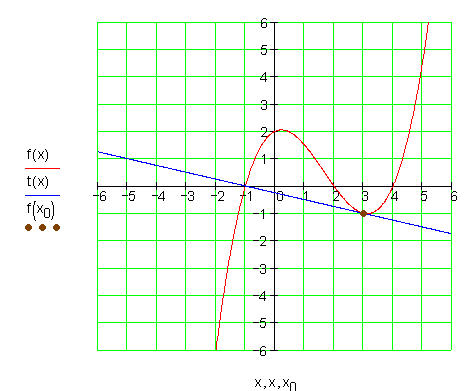
8.
Berechnung: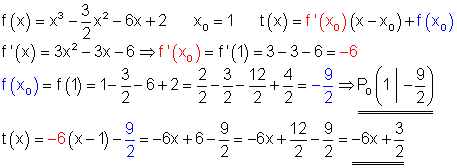
Die Graphen:![]()
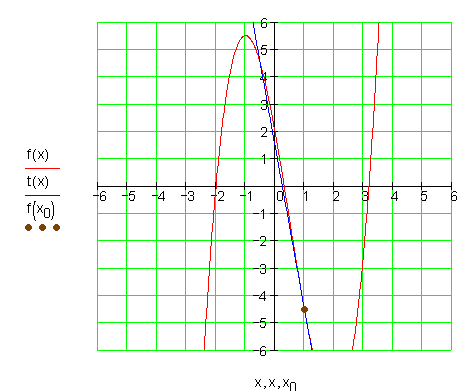
9.
Berechnung: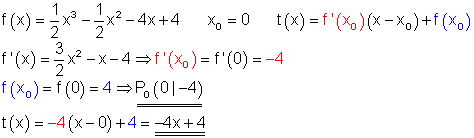
Die Graphen:![]()
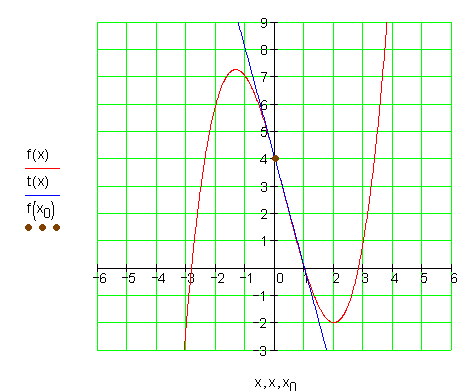
10.
Berechnung: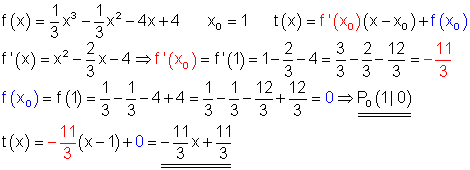
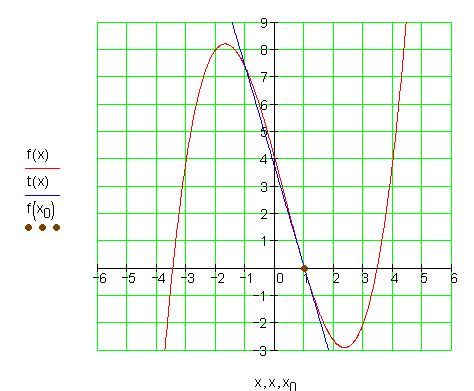
Die Graphen:![]()
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.
Außerdem hier die Playlist aller Videos zur Differentialrechnung.
Dazu kannst du auch den Wikipediaartikel zur Differentialrechnung lesen.