In diesem Beitrag definiere ich zuerst das vektorielle Produkt. Danach erkläre ich, was aus dieser Definition folgt. Danach stelle ich die Rechengesetze dazu vor. Zuletzt zeige ich dies an einigen Beispielen.
Definition: vektorielle Produkt
Wenn wir einen Vektor mit einer Zahl multipliziert, erhalten wir wieder einen Vektor. Diese Art der Multiplikation nennt man S-Multiplikation. Wenn wir jedoch einen Vektor mit einem Vektor multipliziert, ist das Ergebnis eine Zahl, Skalar genannt. Mit anderen Worten eine Skalarmultiplikation.
Darüber hinaus gibt es eine Multiplikationsart, bei der das Ergebnis wieder ein Vektor ist. Diese Art der Multiplikation nennt man Vektormultiplikation, anders ausgedrückt vektorielles Produkt, manchmal auch Kreuzprodukt genannt.
Bevor wir uns mit Anwendungen dieser Multiplikationsart beschäftigen, werde ich zuerst erklären, wie ein solches Produkt definiert ist.
Unter dem vektoriellen Produkt zweier Vektoren \overrightarrow a und \overrightarrow b versteht man einen Vektor, \overrightarrow a \times \overrightarrow b , der durch folgende Bedingungen charakterisiert ist:
1. \overrightarrow a \times \overrightarrow b steht senkrecht auf \overrightarrow a und \overrightarrow b , \\
2. \overrightarrow a , \overrightarrow b und \overrightarrow a \times \overrightarrow b bilden in dieser Reihenfolge ein Rechtssystem. \\
3. | \overrightarrow a \times \overrightarrow b | = | \overrightarrow a | \cdot | \overrightarrow b | \cdot sin(\overrightarrow a , \overrightarrow b) wobei 0 ≤ \measuredangle(\overrightarrow a , \overrightarrow b) ≤ \pi .
Aus obiger Definition folgt:
Das vektorielle Produkt zweier Vektoren hat den Wert Null, wenn wenigsten einer der beiden Vektoren der Nullvektor ist oder wenn die beiden Vektoren parallel sind.
Die Umkehrung gilt ebenfalls: Ist das Vektorprodukt zweier Vektoren, von denen keiner der Nullvektor ist gleich Null, so sind sie parallel.
Aus der 3. Bedingung der Definition folgt, dass ein Vektorprodukt dann seinen größten Wert besitzt, wenn der von ihnen eingeschlossene Winkel 90 grad ist.
Untenstehende Zeichnung verdeutlicht das vektorielle Produkt graphisch:
\overrightarrow a \times \overrightarrow b ist ein Vektor, der auf \overrightarrow a und \overrightarrow b senkrecht steht, sodass \overrightarrow a, \overrightarrow b und \overrightarrow a \times \overrightarrow b ein Rechtssystem bilden .
Sein Betrag ist gleich dem Flächeninhalt des von den beiden Vektoren aufgespannten Parallelelogramms.
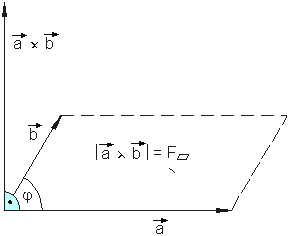
Rechtssystem bedeutet: Dreht man den ersten Vektor im Uhrzeigersinn in Richtung des zweiten, dann bewegt sich der dritte wie eine Schraube mit Rechtsgewinde in seiner Richtung voran.
Rechengesetze für vektorielle Produkte
Für diese Produkte gelten ebenfalls Rechengesetze aus der Algebra:
Satz:

Dazu einige Beispiele:
Beispiel 1:
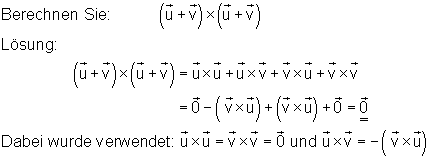
Beispiel 2:
Berechnen Sie formal den Winkel zwischen zwei Vektoren!
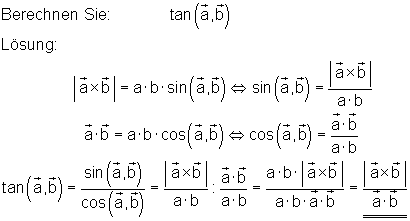
Beispiel 3
Berechnen Sie formal den Winkel zwischen zwei Vektoren!
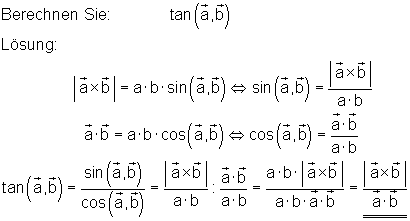
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Vektorrechnung.


