Zinseszinsrechnung Lösungen der Aufgaben I
mit komplettem Lösungsweg

Hier findest du die Lösungen der Aufgaben zur Zinseszinsrechnung. Alle Formeln und  Erklärungen mit ausführlichen Beispielen finden Sie unter Zinseszinsrechnung.

1.

Auf welchen Betrag wachsen folgende Anfangskapitalien an?
a) K(0) = 1800€   p = 5%   n = 10

K(n) = K(0) \cdot q^n  

 q =(1 + \frac {p}{100\%}) = 1 + \frac {5\%}{100\%} = 1,05

K(10) = 1800€ \cdot 1,05^{10} = \underline{\underline{2932,01 €}} 

Antwort: 1.800 € wachsen bei einem Zinssatz von 5% in 10 Jahren auf 2.932,01 € an.
1. b) K(0) = 6000   p = 6,5%   n = 15

K(n) = K(0) \cdot q^n  

 q =(1 + \frac {p}{100\%}) = 1 + \frac {6,5\%}{100\%} = 1,065

K(15) = 6000€ \cdot 1,065^{15} = \underline{\underline{15431,04 €}} 

6.000 € wachsen bei einem Zinssatz von 6,5% in 15 Jahren auf 15.431,04 € an.
1. c) K(0) = 25000   p = 4%    n = 6

K(n) = K(0) \cdot q^n  

 q =(1 + \frac {p}{100\%}) = 1 + \frac {4\%}{100\%} = 1,04

K(6) = 25000€ \cdot 1,04^{6} = \underline{\underline{31632,98 €}} 

25.000 € wachsen bei einem Zinssatz von 4% in 6 Jahren auf 31.632,98 € an.

2.

Ein Vater legte am 01.01. 2006 ein Sparbuch über 1.000 € für seine Tochter an.
Über welchen Betrag kann die Tochter am 31.12. 2021 verfügen, wenn das Sparguthaben mit 3,5% verzinst wird?
K(0) = 1000€    p = 3,5%
Vom 1.1.2006  bis zum 31.12.2021 sind es 16 Jahre, also n = 16

 q =(1 + \frac {p}{100\%}) = 1 + \frac {3,5\%}{100\%} = 1,035

K(16) = 1000€ \cdot 1,035^{16} = \underline{\underline{1733,99 €}} 

Die Tochter kann am 31.12.2021 über einen Betrag von 1.733,99 € verfügen.

3.

Auf welchen Betrag wachsen 16.000 € an, wenn das Guthaben 12 Jahre mit
a) K(0) = 16000   n = 12     = 4%    verzinst wird?

 q =(1 + \frac {p}{100\%}) = 1 + \frac {4\%}{100\%} = 1,04

K(12) = 16000€ \cdot 1,04^{12} = \underline{\underline{25616,52 €}} 

Bei einer 12 jährigen Verzinsung mit 4% wächst das Guthaben auf 25.616,52 € an.
3. b) K(0) = 16000    n = 12    P = 5,5 %    q = 1,055

K(12) = 16000€ \cdot 1,055^{16} = \underline{\underline{30419,32 €}} 

Bei einer 12 jährigen Verzinsung mit 5,5% wächst das Guthaben auf 30.419,32 € an.
3. c) K(0) = 16000   n = 12   p = 8 %    q = 1,08

K(12) = 16000€ \cdot 1,08^{11} = \underline{\underline{40290,72 €}} 

Bei einer 12 jährigen Verzinsung mit 8% wächst das Guthaben auf 40.290,72 € an.

4.

Ein Betrag in Höhe von 6.000 € wurde am 01.01. 2010 zu 4,5% angelegt.
Welche Summe steht dem Anleger am 31.12. 2018 zur Verfügung?
K(0) = 6000   p = 4,5 %   q = 1,045
vom 1.1.2010 bis zum 31.12 2018 sind es 9 Jahre, also n = 9

K(9) = 6000€ \cdot 1,045^{9} = \underline{\underline{8916,57 €}} 

Dem Anleger steht am 31.12.2018 ein Kapital von 8.916,57 € zur Verfügung.

5.

Wie viel Zinsen bringen bei einer 5%igen Verzinsung unter Berücksichtigung von Zinseszinsen 4.000 €, die vom 01.04.2010 bis zum 31.03. 2016 festgelegt wurden?
K (0) = 4000     p = 5 %    q = 1,05
Vom 1.4.2010 bis zum 31.3.2016 sind es 6 Jahre, also n =6

Z = K(6) - K(0) = K(0) \cdot q^6 - K(0)= K(0) \cdot ({q^6-1})=
=  4000€  \cdot (1,05^6 - 1) =\underline{\underline{1360,38€}} 

Die Zinsen betragen 1360,38 €.

6.

Ein Vater möchte, dass seinem Sohn am 31.12. 2020 ein Betrag von 30.000 € ausgezahlt wird.
Welche Summe musste er am 01.01. 2006 anlegen, wenn er mit einer Verzinsung von 5,5% rechnet?
K(15) = 30000€    p = 5,5%    q = 1,055
Vom 1.1.2006 bis zum 31.12.2020 sind es 15 Jahre, also n = 15

K(0) = \frac {K(15)}{q^{15}}=\frac{30000€}{1,055^{15}}

  =\underline{\underline{13437,99€}} 

Es muss eine Summe von K(0) = 13.437,99 € angelegt werden.

7.

Ein junger Mann hat die Wahl zwischen folgenden Kapitalien: 12.000 €, Auszahlung sofort, oder 22.500 €, Auszahlung in 10 Jahren, oder 36.000 €, Auszahlung in 20 Jahren.
Welches Kapital ist, bezogen auf einen gemeinsamen Stichtag am höchsten, wenn man von einer 6%igen Verzinsung ausgeht?
p = 6% Stichtag heute q = 1,06
1. Fall: 12000 € Auszahlung sofort: K(0) = 12000
2. Fall: 22500 € Auszahlung in 10 Jahren

K(0) = \frac {K(10)}{q^{10}}=\frac{22500€}{1,06^{10}}

  =\underline{\underline{12563,88€}} 

3. Fall: 36.000 € Auszahlung in 20 Jahren

Fall 2 beinhaltet das größte Kapital K(0) = 12.563,88 €.

8.

Ein Kapital in Höhe von 5.000 € verdoppelt sich in 12 Jahren.
Welcher Zinssatz liegt bei dieser Berechnung zugrunde.

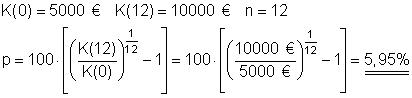
Bei der Berechnung liegt ein Zinssatz von p = 5,95% zugrund.

9.

Zu welchem Zinssatz war ein Kapital von 5.000 € ausgeliehen, wenn es in 5 Jahren auf 6.535 € angewachsen ist?

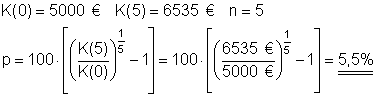
Das Kapital war zu einem Zinssatz von p = 5,5% ausgeliehen.

10.

In wie viel Jahren verdoppelt sich ein Kapital bei einem Zinssatz von 4%?

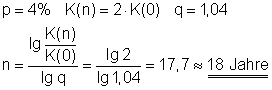
Bei einem Zinssatz von 4% verdoppelt sich das Kapital in etwa 18 Jahren.

11.

In wie viel Jahren wächst ein Kapital von 10.000 € bei einem Zinssatz von 5% auf 14774,55 € an?

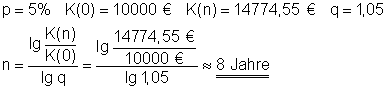
Die Laufzeit beträgt etwa 8 Jahre.

12.

In wie viel Jahren bringt ein Kapital von 15.000 € bei 6%iger Verzinsung 5073,38 € Zinsen?

Die Laufzeit beträgt etwa 5 Jahre.

13.

Ein Kapital hat sich in 9 Jahren verdoppelt.
Zu welchem Prozentsatz wurde es verzinst?

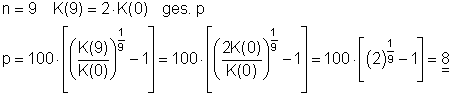
Das Kapital wurde zu 8% verzinst.

14.

Welchen Betrag muss ein Sparer heute bei einer Sparkasse einzahlen, wenn er bei 4,5% Zinsen nach 8 Jahren über 20.000 € verfügen will?

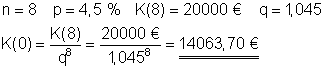
Der einzuzahlende Betrag beläuft sich auf K(0) = 14.063,70 €

15.

Wie lange muss ein Kapital zu 4,5% verzinst werden, bis es seinen dreifachen Wert erreicht hat?

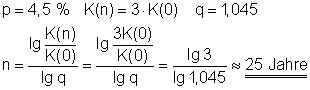
Die Laufzeit beträgt etwa 25 Jahre.

16.

Folgende Kapitalanlagen sind zu berechnen.
a)
K(0) = 10000  €  ;  p = 6 \%   ;  n = 5  ;  q = 1,06
K(5) = K(0) \cdot q^5 = 10000  € \cdot 1,06^5 = \underline{\underline{13382,26 € }}
Nach 5 Jahren steht ein Betrag von 13.382,26 € zur Verfügung.

b)

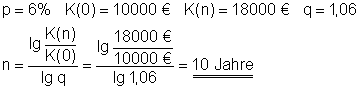
Das Geld steht nach 10 Jahren zur Verfügung.
c)

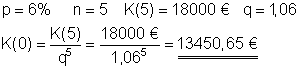
Für den Autokauf müsste ein Betrag von 13.450,65 € angelegt werden.

Hier findest du die Aufgaben.

Hier die Theorie mit ausführlichen Beispielen Zinseszinsrechnung.

Und hier eine Übersicht über alle Beiträge zum Thema Zinsrechnung und zu anderen mathematischen Grundlagen.