In diesem Beitrag erkläre ich leicht verständlich, welche Daten in der Mitte einer Datenreihe liegen. Man nennt diese auch Lagemaße. Zuerst geht es um den Unterschied zwischen dem arithmetischen Mittel einer Datenreihe und einer Häufigkeitstabelle. Danach um Median und Modalwert Dazu stelle ich die Formeln vor und gebe viele Beispiele. Schließlich vergleiche ich Mittelwert, Median und Modalwert. Außerdem erkläre ich das Stängel-Blatt-Diagramm. Am Schluß stelle ich Aufgaben zur Verfügung.
- Arithmetisches Mittel
- Median
- Modalwert (Modus)
- Vergleich Mittelwert, Median, Modalwert
- Daten in einem Stängel-Blatt-Diagramm ordnen
- Link zu Aufgaben
1. Arithmetisches Mittel
Das arithmetische Mittel wird auch Mittelwert und Durchschnitt genannt. Das kennst du sicherlich. In der Statistik unterscheidet man verschiedene:
Formel: Arithmetisches Mittel einer Datenreihe:
Dabei bilden wir die Summe aus allen Beobachtungswerten. Danach teilen wir die Summe durch die Anzahl der Beobachtungswerte.
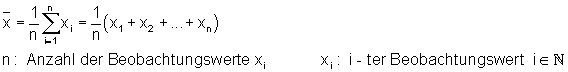
Beispiel:
Hier die Körpergröße aller Schüler einer Klasse. Bilde daraus den Durchschnitt!

Weitere Mittelwerte sind z. B. Durchschnittsnote: 1,8, Durchschnittsalter.
Dazu kannst du dir dieses 📽️Video Mittelwert Datenreihe Häufigkeitstabelle ansehen.
Arithmetisches Mittel aus einer Häufigkeitstabelle
Oben haben wir das arithmetische Mittel einer Datenreihe berechnet. Dazu brauchten wir nur alle Werte addieren und durch deren Anzahl zu dividieren. Denn bei einer Datenreihe steht uns jeder einzelne Beobachtungswert zur Verfügung. Z. b. die Körpergröße jedes einzelnen Schülers. Bei einer Häufigkeitstabelle haben wir nur die Anzahl, wie oft eine Merkmalsausprägung vorkommt. Z. B. haben 5 Schüler die Note 1 erhalten.
Beispiel:
Häufigkeitstabelle
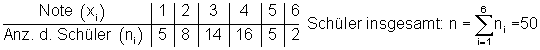
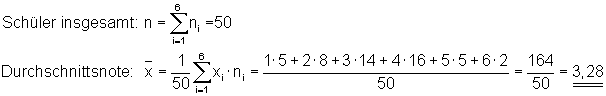
Deshalb multiplizieren wir jede Note mit deren Anzahl. Z. B. haben 8 Schüler eine 2 geschrieben. Also 8 mal 2. Zweitens addieren wir alle Werte der Faktoren. In unserem Beispiele ergibt die Summe 164. Schließlich dividieren wir durch die Anzahl der Klassenarbeiten, hier 50. Das arithmetische Mittel dieser Häufigkeitstabelle beträgt also 3,28.
Man mit der absoluten Häufigkeit rechnen, also der Anzahl der Schüler. Z. B. 5 Schüler haben eine 1 geschrieben. Aber auch mit der relativen Häufigkeit, z. B. ein Zehntel der Schüler haben eine 1 geschrieben. Also 0,1 Schüler.
Hierzu beide Formeln:
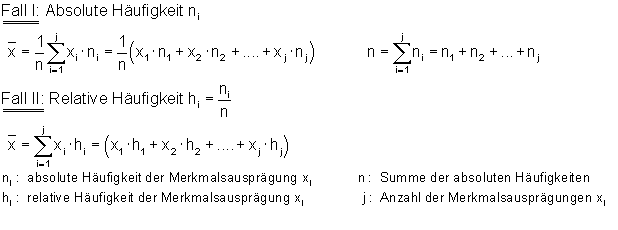
Dazu kannst du dir dieses 📽️Video Mittelwert Datenreihe Häufigkeitstabelle ansehen.
Berechnung des Arithmetischen Mittels bei klassierten Daten
Beispiel:
Wenn wir Daten haben, die schon in Klassen eingeteilt sind, z. B. 11 Schüler haben zwischen 51 und 60 Punkte erhalten, berechnen wir das arithmetische Mittel folgendermaßen: Zuerst bilden wir die Klassenmitte. Dazu addieren wir Klassenanfang und Klassenende und teilen dies durch zwei. Also wie in dem Beispiel 61 + 70 dividiert durch 2 macht 65,5.

Wenn wir dies für alle Klassen durchgeführt haben, bilden wir das arithmetische Mittel wie bei einer normalen Häufigkeitstabelle: Wir multiplizieren jeweils die Klassenmitte mit deren Häufigkeit. Danach addieren wir alle Werte der Faktoren. In unserem Beispiele ergibt die Summe 1728,5. Schließlich dividieren wir durch die Anzahl der der Häufigkeit insgesamt, hier 27. Das arithmetische Mittel dieser klassierten Daten beträgt also 64,0.
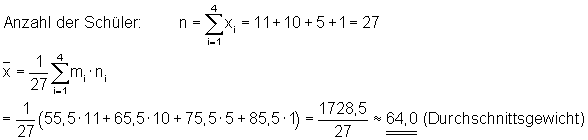
Hier die allgemeine Formel dazu:
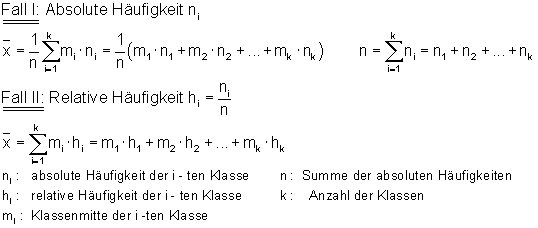
2. Definition: Median
Hierbei ordnen wir alle Werte aus unserem Beispiel der Größe nach und bestimmen die Mitte. Um ihn zu finden addiert man 1 zu der Anzahl der Daten und teilt dies durch 2. In diesem Fall also (15 + 1) / 2 = 8. Also liegt der Median an 8. Stelle.

Wie verändern sich Mittelwert und Median, wenn der größte Schüler die Klasse verlässt und für ihn eine kleine Schülerin mit der Körpergröße 150 dazu kommt?

Wie verändert sich der Median, wenn ein weiterer Schüler mit der Körpergröße 180 dazu kommt?

Allgemeine Rechenvorschrift zur Berechnung des Median:
Wenn die Anzahl n ungerade ist, berechnen wir den Median, indem wir 1 addieren und durch 2 teilen.
Aber wenn die Anzahl n gerade ist, berechnen wir den Median, indem wir durch 2 teilen. Danach adieren wir diesen Wert und den danach und teilen durch 2.

Ergänzungen zum Median
Beispiel:
Ein Bautrupp mit 9 Personen hat folgende monatliche Einkünfte in Euro:
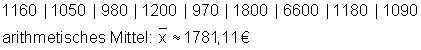
Dieser Durchschnitt liefert ein falsches Bild, weil die Mehrzahl (7 von 9 Personen) höchstens 1200 € verdient. Der Wert 6600 € zieht den Mittelwert hierbei nach oben.
Deshalb sucht man nach einem Wert, der die Verteilung der Einkünfte besser charakterisiert.
Dazu werden die Verdienste der Größe nach sortiert. Dann sucht man den Wert in der Mitte. Hier die Formel dazu:
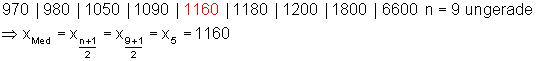
Der Median beschreibt die Verteilung besser als der Mittelwert.
Man nennt ihn auch Zentralwert.
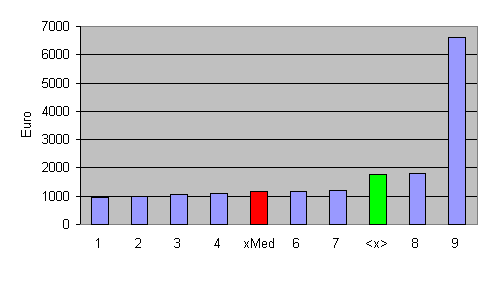
Ausreißer haben auf den Median also keinen Einfluss.
Berechnung des Medians anhand von Beispiel 1:
Wenn die Anzahl n der Merkmalsausprägungen ungerade ist, z.B. das Alter von 7 Mathematiklehrern ( n = 7 )
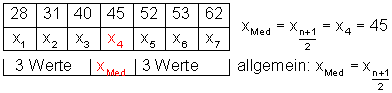
Dann stehen in der Tabelle links und rechts neben dem Median gleich viele Werte.
Beispiel 2:
Wenn die Anzahl der Merkmalsausprägungen gerade ist, z.B. das Alter von 8 Mathematiklehrern ( n = 8 ):
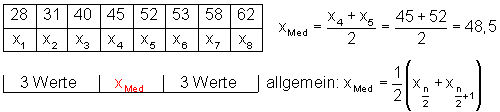
Dann berechnet man den Median aus den beiden mittleren Werten.
Bemerkungen zum Median:
Falls man eine gerade Anzahl eines ordinal skalierten Merkmales hat, existiert der Median nur, wenn beide Merkmalsausprägungen in der Mitte gleich sind. Z. B. bei den Zeugnisnoten 1 2 3 4 5 6 existiert kein Median, denn 3,5 als Zeugnisnote gibt es nicht.
Aber: 1 2 3 3 4 5 hat den Median 3.
Für den Fall, dass metrische Daten in Klassen gruppiert vorliegen, kann die exakte Merkmalsausprägung des Medians nicht bestimmt werden. Z. B. hier:
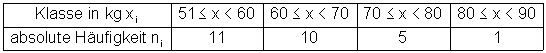
3. Der Modalwert (Modus)
Bei Merkmalsausprägungen wie z.B. „rot, blau, grün“, also bei nominal skalierten Größen kann kein arithmetisches Mittel berechnet werden.
Hier kann man nur fragen, wie häufig die Merkmalsausprägung auftaucht.
Beispiel:
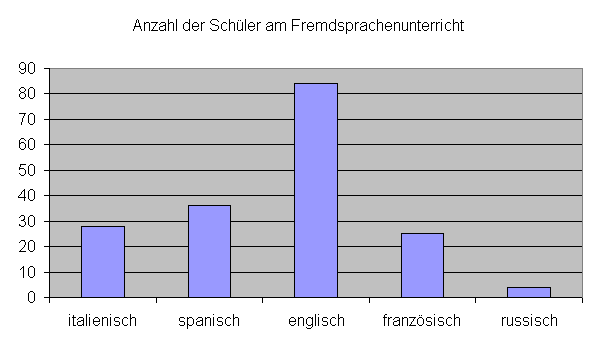
Die Fremdsprache englisch kommt mit der größten Häufigkeit vor (84 mal)
Somit ist der Modalwert xMod = englisch.
Definition Modalwert:
Der Modalwert xMod ist der Merkmalswert, der am häufigsten vorkommt.
Bemerkung zum Modalwert:
Gibt es mehrere Merkmalsausprägungen mit der gleichen maximalen Häufigkeit, so existiert kein Modalwert. Z. B. wenn spanisch und englisch gleich häufig vorkommen.
Wenn man z. B. nicht jedes Gewicht eines Menschen einzeln auflistet, sondern in Klassen zusammenfasst:
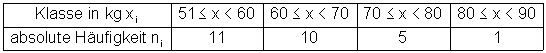
Bei einer solchen Klasseneinteilung ist der Modalwert die Mitte der am dichtesten besetzten Klasse. Also zwischen 51 und 60.
4. Vergleich: Mittelwert, Modalwert, Median
Hier eine Übersicht über diese drei Lagemaße:

Die Noten in dem folgenden Beispiel sind metrisch skaliert, dh. es gibt auch Zwischennoten:
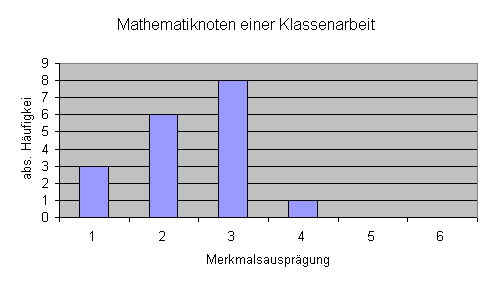
Häufigkeitstabelle:
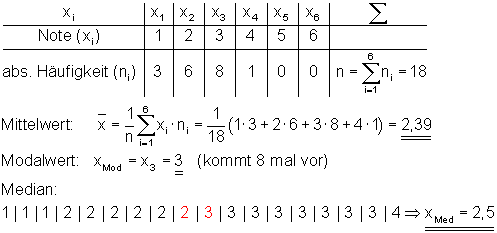
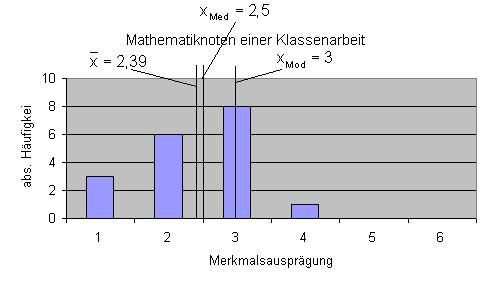
Lagemaße im Säulendiagramm eingezeichnet:
Dann zeichnen wir alle Werte in dem Säulendiagramm ein.
5. Das Stängel-Blatt-Diagramm
Zur Bestimmung des Medians müssen die Daten (Merkmalsausprägungen) geordnet werden. Das kann allerdings mühsam sein. Eine Erleichterung bietet hier das Stängel-Blatt-Diagramm.
Beispiel:
Zuerst sammeln wir die Daten in einer Urliste:
![]()
Danach ordnen wir sie im Stängel-Blatt-Diagramm:

Zuerst ordnet man nach den Stängeln (Zehnerzahlen).
Danach schreibt man die Blätter (Einerzahlen) der Größe nach hinzu.
Die meisten Daten liegen also im 2. Stängel.
Der Wert der größten Häufigkeit (Modalwert) ist xMod = 60
An der 14. Stelle steht der Median xMed = 63
In diesem Beitrag haben wir uns also mit den mittleren Werten einer Datenreihe beschäftigt. Es gibt aber oft einzelne Daten, die stark von allen anderen abweichen. Mit diesen Ausreißern beschäftigen wir uns im Beitrag Spannweite, Median, Varianz und Standardabweichung.
Dazu findest du hier Aufgaben hierzu I.
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik. Dort auch Links zu weiteren Aufgaben.


