Im ersten Beitrag zu Datenerhebung und Darstellung in der Statistik hatten wir gesehen, was Merkmale sind: Eigenschaften der Objekte, z.B. Alter. In diesem Beitrag erkläre ich, dass Merkmale in verschiedenen Ausprägungen vorkommen können, zum Beispiel 13 Jahre. Mit anderen Worten: Merkmale haben Merkmalsausprägungen. Dann werde ich Merkmalsarten definieren. Anschließend werde ich Beispiele für die verschiedenen Merkmalsskalen aufzeigen: Nominalskala, Ordinalskala und metrische Skala. Danach werde ich diskrete und stetige Merkmale vorstellen. Anschließend stelle ich eine Übersicht über alle Merkmalsarten und Merkmalsskalen in einer Grafik auf. Schließlich wiederhole ich alle Definitionen.
- Definition Merkmalsausprägung und Merkmalsarten
- Merkmalsskalen
- Diskrete und stetige Merkmale
- Übersicht: Merkmalsarten und Merkmalsskalen
- Definitionen
Beispiel Merkmalsart, Merkmal, Merkmalsausprägung:

Geschlecht und Farbe sind dabei qualitative Merkmale, es gibt keine Rangfolge.
Körpergröße, Bruttoverdienst und Körpergewicht sind jedoch quantitative Merkmale, sie lassen sich vergleichen.
Definition Merkmalsarten:
Merkmalsarten bedeutet: Man unterscheidet zwei Arten von Merkmalen: qualitative = ohne Rangfolge und quantitative = messbare Merkmale.
Merkmalsskalen
Merkmalsausprägungen bilden eine Skala. Je nach Merkmal und Ausprägung unterscheidet man folgende Skalen:
Nominalskala Beispiel:

Bei einer Nominalskala (Namensskala) sind die Merkmalsausprägungen nur Namen und Bezeichnungen, sie dienen der Kennzeichnung.
Die Merkmalsausprägungen lassen sich jedoch nicht ordnen oder vergleichen. Z. B. ist es schwierig, Buntstifte nach deren Helligkeit zu ordnen. Aber ist ein dunkles Rot heller als ein helles Grün?
Ordinalskala Beispiel:

Bei einer Ordinalskala lassen sich die Merkmalsausprägungen jedoch ordnen und miteinander vergleichen. Z. B. ist die Schuhgröße 41 größer als 40.
metrische Skala Beispiel:
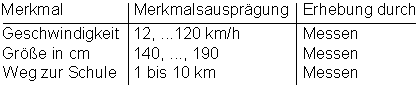
Bei einer metrischen Skala sind die Merkmalsausprägungen übrigens reelle Zahlen. Das heißt, sie können negativ sein und man kann sie beliebig unterteilen. Z. B. Temperatur.
Diskrete und stetige Merkmale
Merkmale können in diskreter oder stetiger Form vorliegen.
Diskrete Merkmale können dabei abzählbar viele Merkmalsausprägungen annehmen. Z. B. ist eine Frau entweder schwanger oder nicht. Es gibt dabei keine Nachkommastellen, ein bisschen schwanger gibt es nicht. 😉
Stetige Merkmale können jedoch jeden beliebigen Wert in einem Bereich (Intervall) annehmen. Z. B. kann man das Alter eines Menschen auch mit 10,5 Jahren angeben.
Beispiele:

Nominal – und ordinalskalierte Merkmale sind stets diskrete Merkmale.
Metrisch skalierte Merkmale können dagegen stetig oder diskret sein.
Übersicht Merkmalsarten und Merkmalsskalen
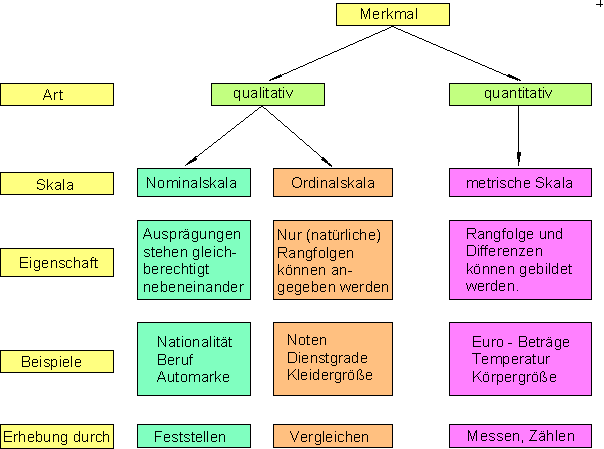
Alle Definitionen
- Deskriptive Statistik: Beschreibende Statistik, Erhebung, Aufbereitung, Darstellung und Beschreibung statistischer Daten
- Grundgesamtheit: Gesamtheit aller möglichen Untersuchungseinheiten aller Merkmalsträger, die Gegenstand einer statistischen Untersuchung sind.
- Merkmalsträger: Befragte Personen oder untersuchte Objekte, an denen etwas gezählt, gemessen oder beobachtet wird.
- Merkmal: Eigenschaft der Merkmalsträger, die Gegenstand derBefragung, Zählung oder Messung ist.
- Merkmalsausprägung: Merkmalswert, der Wert, der bei der Erhebung beim Merkmalsträger festgestellt wird. Jedes Merkmal hat zwei oder mehr Ausprägungen.
- Merkmalsskala: Sie beinhaltet alle möglichen Ausprägungen eines Merkmals; die Skala ist das Hilfsmittel, mit dem die Merkmalswerte gemessen oder erfragt werden.
- Merkmalsarten: Einteilung in quantitative und qualitative Merkmale.
- Stichprobe: Teilmenge der Grundgesamtheit.
Hier findest du Aufgaben hierzu.
Im nächsten Beitrag werden wir schließlich sehen, wie man in der Statistik Mittelwert, Median und Modalwert berechnet.
Alle Formeln zur beschreibenden Statistik sind hier übersichtlich zusammengestellt.
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik, dort auch Links zu weiteren Aufgaben.


