In der Statistik werden Daten erhoben, aufbereitet und analysiert, mit anderen Worten Datenerhebung. Damit man einen Überblick über große Datenmengen bekommt, kann man sie mit verschiedenen Methoden darstellen und analysieren.
In diesem Beitrag gebe ich eine Einführung in die beschreibende Statistik. Dabei geht es um das Sammeln und darstellen der Daten. Zuerst definiere ich die Begriffe Stichprobe, Urliste, Rohdaten, Erhebungsumfang, Merkmale, Merkmalsausprägung und Klasseneinteilung. Danach stelle ich die Aufbereiten der Daten und ihre Darstellung vor. Dazu muss man die Häufigkeit bestimmter Merkmalsausprägungen ermitteln. Anschließend stelle ich die verschiedenen grafischen Darstellung vor: Punktdiagramm (Streudiagramm), Säulendiagramm und Doppelsäulendiagramm und vergleiche sie.
- Definitionen
- Aufbereiten der Daten und ihre Darstellung
- Grafische Darstellung durch ein Säulendiagramm
- Darstellung im Punktdiagramm (Streudiagramm)
- Klasseneinteilung
- Grafiken im Vergleich
- Weitere Darstellungsarten im Säulendiagramm
- Weiteres Beispiel zur Klasseneinteilung
Beispiel für die Datenerhebung:
Wenn man z. B. wissen will, ob die Jugend wird immer dicker wird, kann man nicht alle Jugendlichen befragen. Sondern man befragt nur einen Teil der Gesamtheit.
Definition Datenerhebung per Stichprobe:
Wenn man einen Teil einer Gesamtheit befragt, dann spricht man bei der Datenerhebung von einer Stichprobe.
Definition Urliste:
Das Ergebnis der Stichprobe wird dann in einer Urliste festgehalten.
Zum Beispiel in dieser Urliste:
| Schüler
Nr. |
Ge-schlecht | Körper-
größe in cm |
Gewicht
in kg |
Rau-
cher |
Sport-
art |
||
| w | m | ||||||
| 01 | x | 160 | 52 | x | Hand-
ball |
||
| 02 | x | 172 | 67 | x | Fuß-
ball |
||
| 03 | x | 180 | 60 | x | Golf | ||
| … | … | … | … | … | … | … | … |
| xx | x | 170 | 65 | x | Judo |
Dabei sollte man eine solche Urliste anonym erstellen.
Definition Rohdaten:
Damit sind alle in der Urliste enthaltenen Daten gemeint.
Definition Erhebungsumfang:
Dabei handelt es sich um die Anzahl der untersuchten Objekte (hier Schüler).
Werden z. B. 27 Schüler befragt, so sagt man, „Die Anzahl der Merkmalsträger ( n = 27 ) bildet den Erhebungsumfang“.
Definition Merkmale:
Mit anderen Worten die Eigenschaften der Objekte. (z.B. Geschlecht, Körpergröße, Gewicht, Raucher, Sportart, …)
Definition Merkmalsausprägung xi:
Ein Merkmal kann dabei in verschiedenen Ausprägungen vorkommen (z. B. Geschlecht m oder w).
Zum Beispiel:
| Merkmal | Merkmalsausprägung xi |
| Geschlecht | männlich, weiblich |
| Körpergröße | 160 cm, 182 cm, 154 cm, 163 cm, … |
| Körpergewicht | 52 kg, 81 kg, 71 kg , ….. |
| Raucher | ja, nein |
| Sportart | Judo, Tischtennis, Fußball, … |
Vorgehen bei statistischen Datenerhebungen
Wenn man Daten erhebt, will man feststellen, wie die verschiedenen Ausprägungen eines Merkmals in einer Stichprobe verteilt sind.
Vor der Erhebung muss man deshalb einige Fragen klären.
Zum Beispiel: Wonach soll gefragt werden?
Welche Antworten sind möglich?
Welchen Umfang soll die Stichprobe haben?
Aufbereiten der Daten und ihre Darstellung
Ermittlung der Häufigkeit bestimmter Merkmalsausprägungen
In einer Strichliste werden Merkmalsträger mit gleichen Merkmalsausprägungen für ein bestimmtes Merkmal zusammengefasst.
Bearbeitung des Merkmals Sportart
Z. B. bei sehr vielen Sportarten sind diese in Klassen zusammenfassen.
Strichliste:
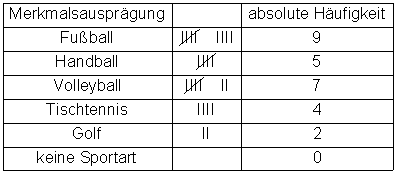
Der Merkmalsausprägung z. B. Fußball wird hier die absolute Häufigkeit 9 zugeordnet.
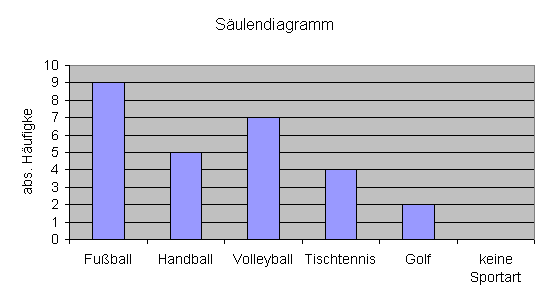
Grafische Darstellung durch ein Säulendiagramm
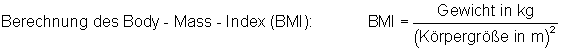
Wertung:

Auszug aus der Urliste einer Erhebung mit Berechnung des BMI:
| Schüler Nr. |
Ge-
schlecht |
Körper-
größe |
Gewicht in kg |
BMI | Wertung | |
| w | m | |||||
| 01 | x | 160 | 52 | 20,3 | normal | |
| 02 | x | 172 | 67 | 22,6 | normal | |
| 03 | x | 180 | 60 | 18,5 | Untergewicht | |
| 04 | x | 167 | 55 | 19,7 | Untergewicht | |
| 05 | x | 178 | 63 | 19,9 | Untergewicht | |
| 06 | x | 175 | 63 | 20,6 | normal | |
| 07 | x | 183 | 70 | 20,9 | normal | |
| 08 | x | 188 | 78 | 22,1 | normal | |
| 09 | x | 181 | 84 | 25,6 | Übergewicht | |
| 10 | x | 183 | 68 | 20,3 | normal | |
| 11 | x | 162 | 63 | 24,0 | normal | |
| 12 | x | 171 | 57 | 19,5 | Untergewicht | |
| 13 | x | 177 | 67 | 21,4 | normal | |
| 14 | x | 165 | 58 | 21,3 | normal | |
| 15 | x | 174 | 70 | 23,1 | normal | |
| 16 | x | 179 | 73 | 22,8 | normal | |
| 17 | x | 175 | 55 | 18,0 | Untergewicht | |
| 18 | x | 183 | 72 | 21,5 | normal | |
| 19 | x | 163 | 51 | 19,2 | Untergewicht | |
| 20 | x | 163 | 60 | 22,6 | normal | |
| 21 | x | 165 | 64 | 23,5 | normal | |
| 22 | x | 171 | 51 | 17,4 | Untergewicht | |
| 23 | x | 175 | 54 | 17,6 | Untergewicht | |
| 24 | x | 176 | 68 | 22,0 | normal | |
| 25 | x | 184 | 75 | 22,2 | normal | |
| 26 | x | 185 | 76 | 22,2 | normal | |
| 27 | x | 169 | 59 | 20,7 | normal |
BMI – Auswertung:

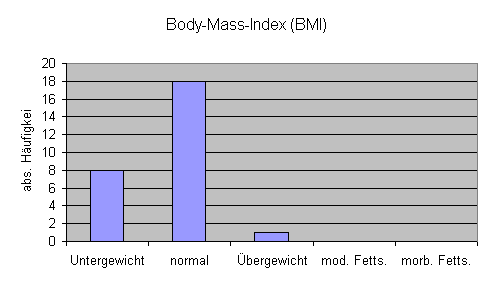
Bearbeitung des Merkmals Gewicht.
Auszug aus der Urliste: (Wertetabelle)
![]()
Darstellung im Punktdiagramm (Streudiagramm)
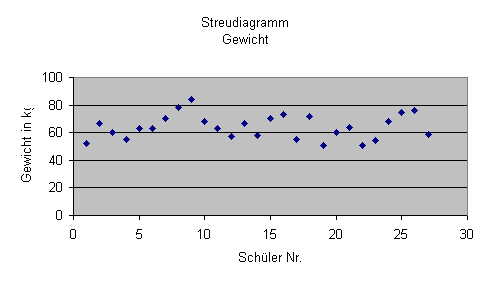
Wenn man Schüler den Gewichten zuordent, erhöht man die Übersichtlichkeit nicht wesentlich.
Man kann jedoch sofort ablesen, dass das Gewicht aller Schüler zwischen 40 kg und 100 kg liegt.
Eine Strichliste zur Bestimmung der Häufigkeit einer bestimmten Merkmalsausprägung macht hier also keinen Sinn.
Danach teilen wir die Merkmalsausprägungen in Klassen ein. Wir wählen 4 Klassen mit einer Klassenbreite von 10 kg. In jeder davon ordnen wir die Körpergewichte ein.
Für das Merkmal Gewicht haben wir nun als Ausprägungen die Klassen I bis IV.
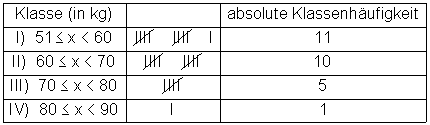
Definition Klasseneinteilung:
Wenn man verschiedene Merkmalsausprägungen zu einer neuen Ausprägung zusammenfasst, spricht man von einer Klasseneinteilung der Stichprobenwerte.
Dies kann man dann in einem Säulendiagramm ohne Lücken darstellen.
Häufigkeitstabelle:
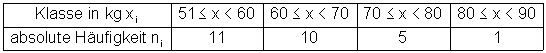
Grafische Darstellung der Häufigkeitsverteilung der Klassen
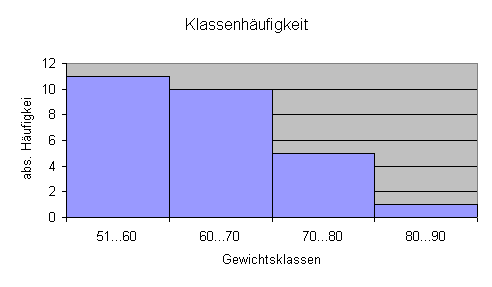
Wir haben die Klassenbreite (10 kg) willkürlich festgelegt.
Nun halbieren wir die Klassenbreite.
Damit vergrößert sich die Anzahl der Klassen.
Häufigkeitstabelle:

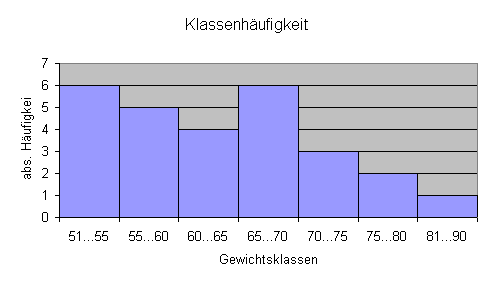
Grafiken im Vergleich:
Je geringer die Anzahl der Klassen, desto besser ist die Übersichtlichkeit.
Der Informationsgehalt wird aber geringer (Hier kann man manipulieren).
Es gibt keine allgemein gültige Festlegung der Klassenbreite, deshalb muss man eine sinnvolle Klassenbreite für die Häufigkeitstabelle wählen.
Üblich ist ein Wert zwischen 5 und 10.
Weitere Darstellungsarten im Säulendiagramm:
Um die Unterschiede der Körpergewichte von Schülern und Schülerinnen aufzuzeigen, listet man die Häufigkeitstabelle mit der Klassenbreite 10 kg nach männlich und weiblich auf.
Häufigkeitstabelle:

Säulendiagramm für zwei Verteilungen:
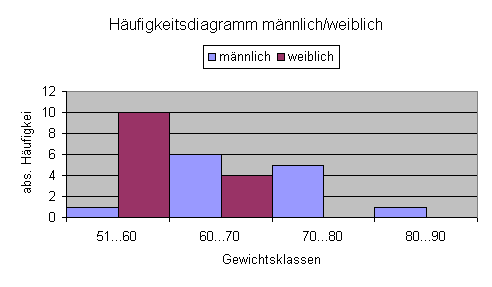
Doppelsäulendiagramm:
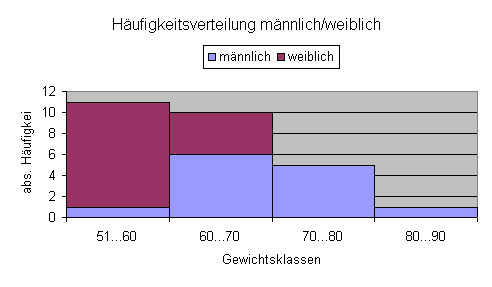
Die Körpergewichte der Schülerinnen verteilen sich nur auf die ersten beiden Klassen, während 6 von 13 Schülern ein Gewicht von mehr als 70 kg haben.
![]()
Weiteres Beispiel zur Klasseneinteilung
In einer Klasse mit 32 Schülern misst jeder Schüler seine Pulsfrequenz.
Die Erhebungsdaten tragen wir danach in eine Urliste ein.
Zur Bestimmung der Klassenbreite und damit der Anzahl der Klassen ist es sinnvoll, in der Urliste den kleinsten und den größten Wert zu markieren.

Klassenbreite 4 ergibt 10 Klassen.
![]()
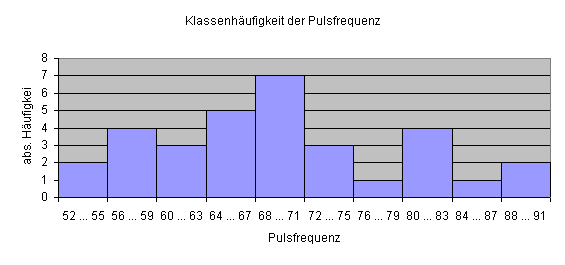
Klassenbreite 8 ergibt 5 Klassen.

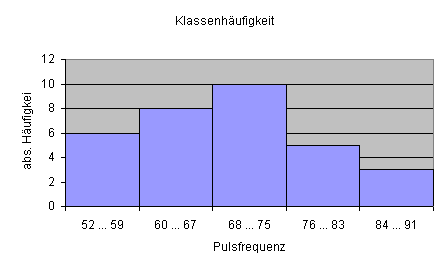
Im nächsten Beitrag werden wir näher betrachten, wie man von einer Urliste zu einer Grafik kommt und einen Überblick über die verschiedenen Darstellungsformen in der Statistik kennenlernen.
Hier findest du Aufgaben hierzu: Merkmale.
Alle Formeln zur beschreibenden Statistik sind hier übersichtlich zusammengestellt.
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik, dort auch Links zu weiteren Aufgaben.


