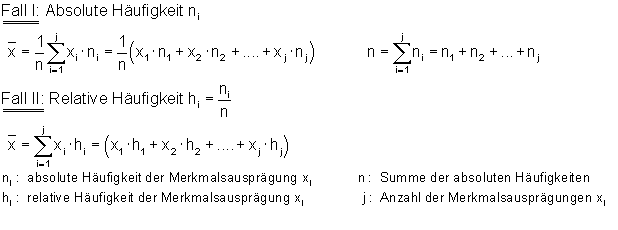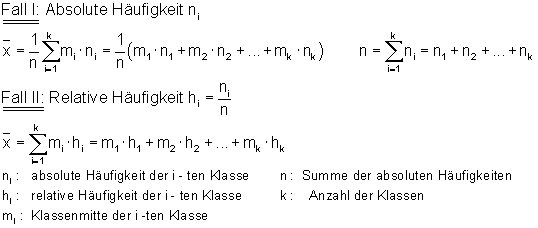Hier findest du eine Statistik Formelsammlung mit Beispielen.
- Das arithmetische Mittel
- Mittelwert
- Median
- Spannweite
- Quartilsabstand
- Varianz und Standardabweichung
- Links zu Aufgaben
Das arithmetische Mittel
Arithmetisches Mittel einer Datenreihe
Das arithmetischen Mittel berechnet man folgendermaßen aus einer Datenreihe:
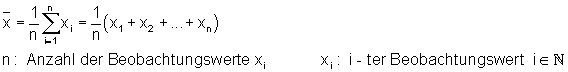
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Arithmetisches Mittel aus einer Häufigkeitstabelle
Das arithmetischen Mittel berechnet man folgendermaßen aus einer Häufigkeitstabelle. Dabei muss man zwischen der absoluten und der relativen Häufigkeit unterscheiden:
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Mittelwert bei klassierten Daten aus einer Häufigkeitstabelle
Den Mittelwert bei klassierten Daten berechnet man folgendermaßen aus einer Häufigkeitstabelle:
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Der Median
Den Median berechnet man folgendermaßen:
Wenn n die Anzahl der Beobachtungswerte x_i ist, dann gilt:
n ungerade \Rightarrow x_{Med} = x_{\frac{n + a}{2}} \\
n gerade \Rightarrow x_{Med} = \frac{1}{2} (x_{\frac{n}{2}} + x_{\frac{n}{2}+1})
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Mittelwert-Median-Modalwert
Die Spannweite
Die Spannweite berechnet man folgendermaßen:
Spannweiter = größter Beobachtungswert – kleinster Beobachtungswert
R = x_{max} - x_{min}
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Der Quartilsabstand
Berechnung des Quartilsabstands
Der mittlere 50 %-Bereich aller Beobachtungswerte heißt Quartilabstand. Man berechnet ihn folgendermaßen:
Q_A = Q_3 - Q_1
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Varianz und Standardabweichung
Varianz einer Datenreihe
Die Varianz aus einer Datenreihe berechnet man wie folgt:
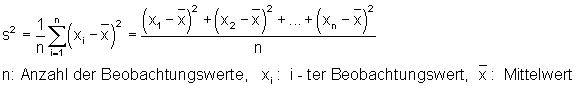
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Die Standardabweichung berechnet man folgendermaßen:
S = \sqrt{s^2} = \sqrt{Varianz}
Berechnung der Varianz einer Häufigkeitstabelle
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Berechnung der Varianz einer klassierten Häufigkeitstabelle
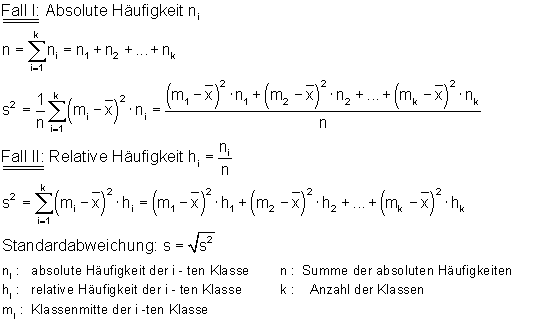
Hier findest du die Erklärungen, viele Beispiele und Links zu Aufgaben:
Spannweiter, Median, Varianz und Standardabweichung
Aufgaben hierzu Statistik vermischte Aufgaben.
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik, dort auch Links zu weiteren Aufgaben.
123mathe-Videos jetzt auch auf 📽️ Humix.
