In diesem Beitrag findest du die Lösungen zu den Aufgaben Flächen zwischen Funktionsgraphen. Mit komplettem Lösungsweg.
Aufgabenstellung:
Bestimme die Flächen zwischen folgenden Funktionsgraphen. Zeichne danach beide Graphen in ein Koordinatensystem. Schraffiere schließlich die berechnete Fläche.
Dazu kannst du dir das 📽️Video Integral Fläche zwischen Graphen ansehen.
1. Ausführliche Lösung:
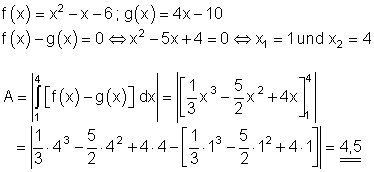
Die Fläche zwischen den beiden Graphen beträgt 4,5 FE.
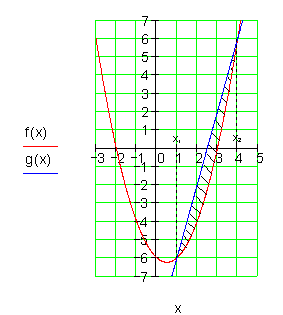
2. Ausführliche Lösung:
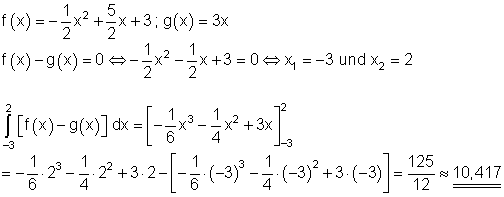
Die Fläche zwischen den beiden Graphen beträgt etwa 10,417 FE.
Bemerkung: Man kann die Rechnung auch ohne Beträge durchführen, wenn man von dem Ergebnis, falls es einen negativen Wert hat, den Betrag bildet.

3. Ausführliche Lösung:
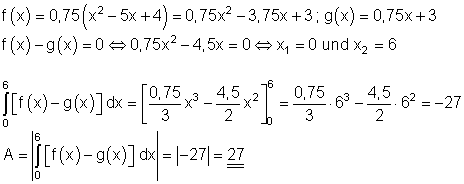
Die Fläche zwischen den beiden Graphen beträgt 27 FE.

4. Ausführliche Lösung:
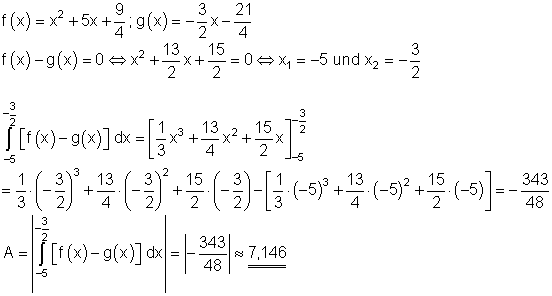
Die Fläche zwischen den beiden Graphen beträgt etwa 7,146 FE.
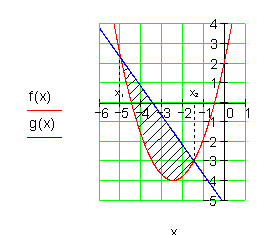
5. Ausführliche Lösung:
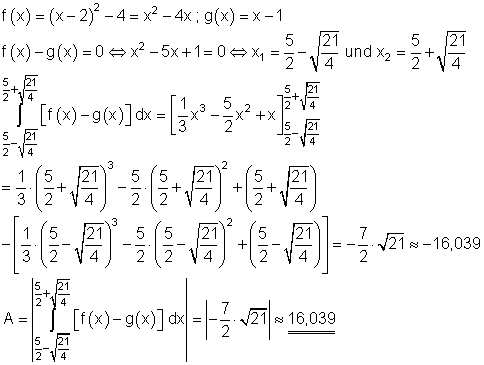
Die Fläche zwischen den beiden Graphen beträgt etwa 16,039 FE.
6. Ausführliche Lösung:
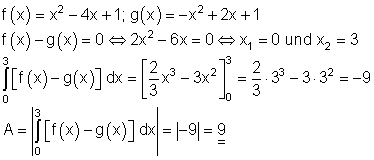
Die Fläche zwischen den beiden Graphen beträgt 9 FE.
7. Ausführliche Lösung:
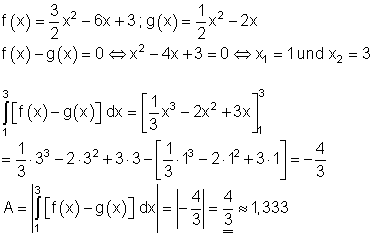
Die Fläche zwischen den beiden Graphen beträgt etwa 1,333 FE.
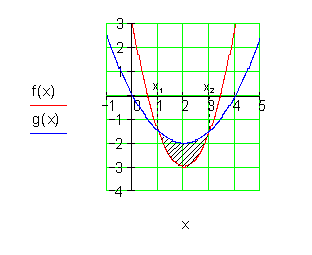
8. Ausführliche Lösung:
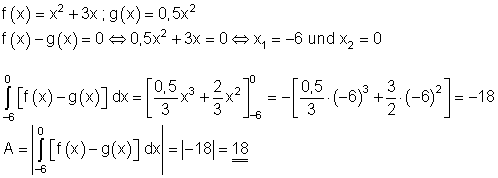
Die Fläche zwischen den beiden Graphen beträgt 18 FE.
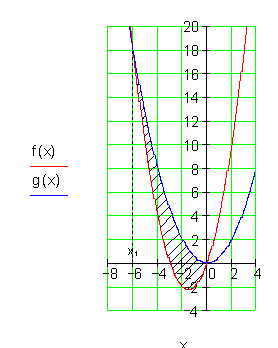
9. Ausführliche Lösung:
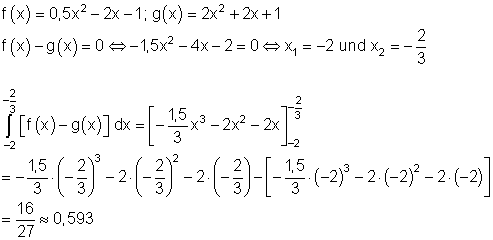
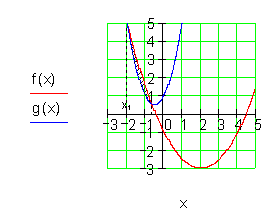
Die Fläche zwischen den beiden Graphen beträgt etwa 0,593 FE.
10. Ausführliche Lösung:
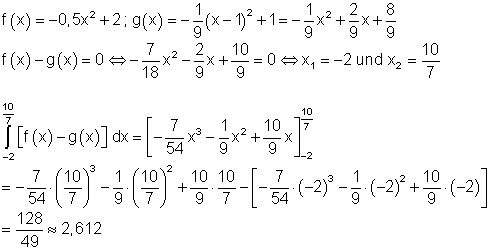
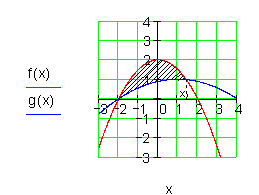
Die Fläche zwischen den beiden Graphen beträgt etwa 2,612 FE.
Hier findest du die Theorie und Aufgaben hierzu.
Und hier eine Übersicht über alle Beiträge zur Integralrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.

