Bei bisherigen Rechnungen spielte lediglich die Anordnung der beteiligten Vektoren zueinander eine Rolle. Die räumliche Lage der Vektoren war dabei unwesentlich. Das lässt die Schlussfolgerung zu, dass die Vektorrechnung unabhängig von einem Koordinatensystem ist. Für bestimmte Probleme ist es dennoch nützlich, wenn man für die Darstellung der Vektoren ein Koordinatensystem zugrunde legt.
Deshalb geht es in diesem Beitrag um die Komponentendarstellung von Vektoren. Für weitere Betrachtungen lege ich das räumliche kartesische Koordinatensystem zugrunde. Dabei handelt es sich um drei senkrecht aufeinander stehende Koordinatenachsen, die der Reihe nach mit x1, x2 und x3 bezeichnet werden.
Statt x1, x2 und x3 könnte man diese auch x, y und z-Achse nennen, für die Darstellung n-dimensionaler Vektoren wäre das jedoch wenig geeignet.
Das räumliche kartesische Koordinatensystem
Nachfolgend zwei Darstellungen für das räumliche kartesische Koordinatensystem, wie es in der Praxis oft verwendet wird.
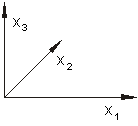
Die x1 und x3 -Achse liegen in der Zeichenebene. Die positive x2 -Achse zeigt nach hinten.
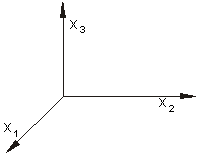
Die x2 und x3-Achse liegen in der Zeichenebene. Die positive x1-Achse zeigt nach vorne.

Jede der drei Komponenten kann man auch als Vielfaches des jeweiligen Einheitsvektors darstellen:
![]()
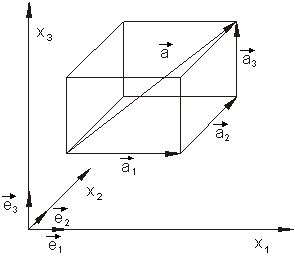
Die drei Skalare a1 , a2 und a3 , die die Länge des Vektors in Richtung der Koordinatenachsen angeben, nennt man Koordinaten des Vektors.
Beispiel 1 für die Komponentendarstellung:
![]()
soll in ein räumliches kartesisches Koordinatensystem eingezeichnet werden.
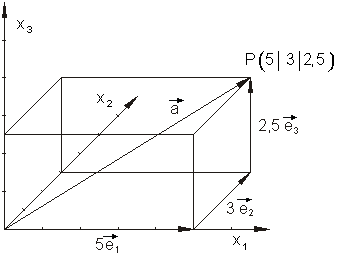
Um den Vektor darzustellen, legen wir dessen Anfangspunkt in den Koordinatenursprung.
Danach setzten wir den Vektor nach den Regeln der Vektoraddition aus seinen Komponenten zusammen.
In diesem Beispiel endet der eingezeichnete Vektor in dem Punkt P, der die Koordinaten P( 5| 3 |2 ,5 ) hat.
Das Beispiel zeigt:
Jeder Vektor, der im dreidimensionalen Raum vom Koordinatenursprung ausgeht, endet dort in einem Punkt. So wie jeder Punkt im dreidimensionalen Raum eindeutig durch seine Koordinaten festgelegt ist, kann dieses auch durch Vektoren geschehen, die vom Koordinatenursprung zu diesem Punkt führen. Solche Vektoren nennt man Ortsvektoren.
Der Vektor \overrightarrow r = 5 \overrightarrow e_1 + \overrightarrow 3e_2 + 2,5 \overrightarrow e_3 endet im Punkt P(5|3|2,5).
Allgemein gilt: \overrightarrow r = x_1 \overrightarrow e_1 + x_2 \overrightarrow e_2 + x_3 \overrightarrow e_3 endet im Punkt P(x1|x2|x3).
Da Größe und Richtung eines Vektors im dreidimensionalen Raum eindeutig durch die Angabe der drei Koordinaten festgelegt ist, kann man beim Aufschreiben eines Vektors auf die Angabe der Einheitsvektoren verzichten. Ein Vektor lässt sich unter dieser Vorraussetzung auch als Spaltenmatrix schreiben.
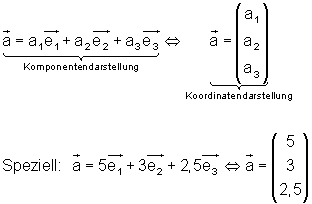
Die Komponentendarstellung und die Koordinatendarstellung sind zwei unterschiedliche aber gleichwertige Schreibweisen für Vektoren.
Ein Ortsvektor, der zum Punkt P führt, wird wie folgt dargestellt:
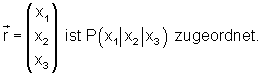
Man sollte darauf achten, dass Ortsvektoren, die als gebundene Vektoren vom Koordinatenursprung zu einem Punkt führen, nicht mit freien Vektoren, die im Raum beliebig parallel zu sich verschoben werden dürfen, verwechselt werden.
Beispiel 2
Wir wollen einen Würfel mit der Kantenlänge 8 LE so in ein räumliches kartesisches Koordinatensystem einzeichnen, dass eine Ecke im Koordinatenursprung liegt. Zu allen Eckpunkten des Würfels wollen wir danach Ortsvektoren zeichnen. Die Ortsvektoren wollen wir in Koordinatendarstellung angeben.
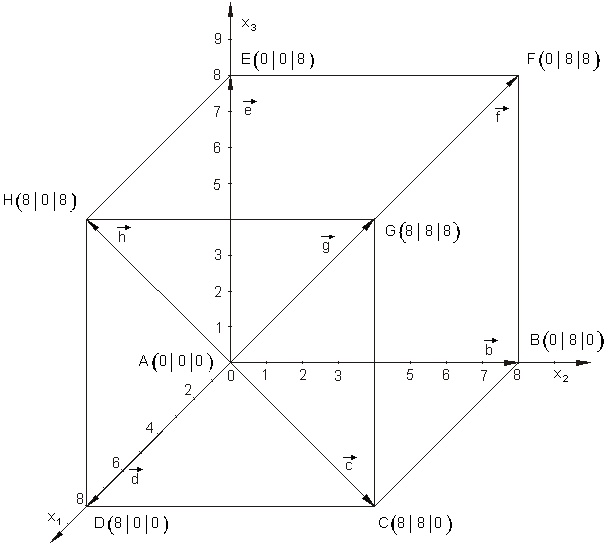
Für die Ortsvektoren gilt:
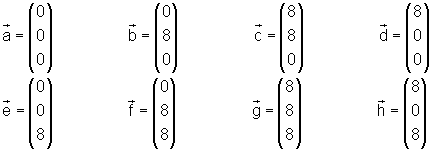
Die obige Darstellung ist eine von vielen Möglichkeiten. Der Würfel liegt im 1. Oktanten. Eine andere Darstellung könnte in einem Koordinatensystem erfolgen, in dem die x1-Achse nach hinten zeigt. Je nach Bezeichnung der Eckpunkte des Würfels und dessen Ausrichtung würden die Vektoren andere Bezeichnungen bekommen und auch andere Koordinaten haben können.
Hier findest du eine Übersicht über alle Beiträge und Aufgaben zum Thema Vektorrechnung.


