Hier findest du die Lösungen zu den Aufgaben zum Hypothesentest I. Darin geht es unter anderem: Bestimme den Annahme- und Ablehnungsbereich, sowie den tatsächlichen Fehler 1. Art. Skizziere grob die Verteilungsfunktion und kennzeichne die markanten Punkte.
1.
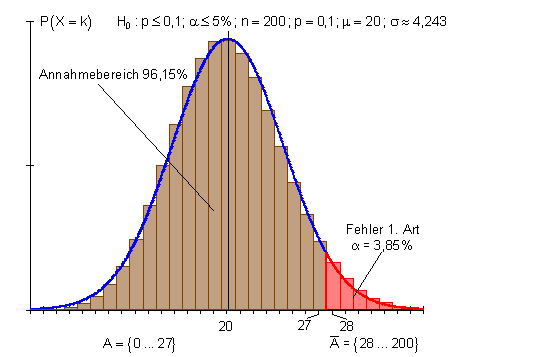
Eine Fernsehserie hatte im letzten Jahr eine mittlere Einschaltquote von 10%. Das Management des Senders vermutet, dass die Beliebtheit der Serie im letzten Quartal des Vorjahres sogar etwas zugenommen hat. Wenn die Beliebtheit der Sendung tatsächlich zugenommen hat, wollen sie weitere Serien dazu kaufen. Dazu wollen sie 200 Personen mittels einer Telefonaktion befragen. Man ist sich auch der Zufälligkeit von Stichprobenergebnissen bewusst und gibt sich mit einer Sicherheit von mindestens 95% des Befragungsergebnisses zufrieden.
Bestimme den Annahme- und Ablehnungsbereich, sowie den tatsächlichen Fehler 1. Art. Skizziere grob die Verteilungsfunktion und kennzeichne die markanten Punkte.
1. Ausführliche Lösung
Aufgabenanalyse und aufstellen der Hypothesen
Man möchte überprüfen, ob die Beliebtheit der Sendung zugenommen hat, ob also die Vermutung p > 0,1 zutrifft. Bei der Aufstellung der Hypothesen geht man so vor:
Das was gezeigt werden soll, bildet die Alternativhypothese, das Gegenteil davon die Nullhypothese.
Nullhypothese H0: p ≤ 0,1; Alternativhypothese H1: p > 0,1.
Bei Ablehnung der Nullhypothese nimmt man die Alternativhypothese an.
H0 wollen wir mit die Umfrage testen.
Eine Sicherheit von 95% bedeutet, mit einer Wahrscheinlichkeit von 5% ist die Ablehnung der Nullhypothese eine Fehlentscheidung. Signifikanzniveau 5%.
Auf dieser Grundlage legen wir für H0 einen Annahmebereich und ein Ablehnungsbereich fest. Da große Werte gegen H0 sprechen, handelt es sich um einen rechtsseitigen Test.

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50
Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 findest du hier.
Dort findest du auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.
Auswertung:
Würde bei der Umfrage herauskommen, dass mehr als 27 Personen die Sendung sehen möchten, dann fiele das in den Ablehnungsbereich von H0. Die Nullhypothese würde man ablehnen. Die Alternativhypothese H1: p > 0,1 würde man annehmen. Danach würden man neue Serien kaufen.
Der Fehler, den man bei dieser Entscheidung gemacht hätte, beträgt 3,85%. Das bedeutet, mit einer Wahrscheinlichkeit von 3,85% würde man die Hypothese H0 zu unrecht ablehnen. Die Fehlerwahrscheinlichkeit (3,85%) heißt Irrtumswahrscheinlichkeit. Statt Irrtumswahrscheinlichkeit sagt man auch Signifikanzniveau. Käme bei der Umfrage heraus, dass höchstens 27 Personen die Sendung sehen möchten, dann würde man die Hypothese H0 annehmen und alles bliebe beim alten. Man würden dann keine neuen Serien dazu kaufen.
Da der Ablehnungsbereich der H0 Hypothese im rechten Bereich der Wahrscheinlichkeitsverteilung liegt, nennt man diesen Hypothesentest auch rechtsseitigen Test.
2.
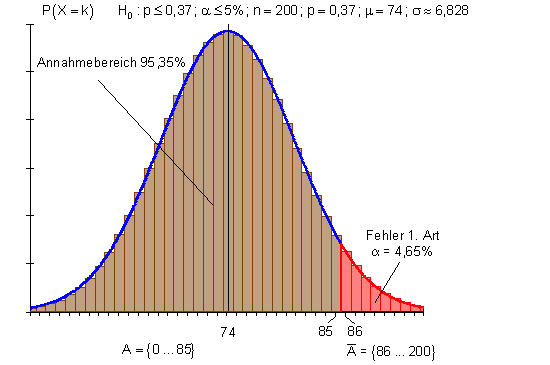
In einer Kleinstadt gibt es 2 Grundschulen. Der Schulleiter der Bismarckschule bestreitet, dass im kommenden Schuljahr wieder nur 37% aller Einschulungen an seine Schule kommen. Man habe die Schule schließlich durch viele Zusatzangebote attraktiver gemacht. Eine Meinungsumfrage mit 200 Eltern soll zeigen, dass die Beliebtheit der Schule gestiegen ist.
Bestimme den Annahme- und Ablehnungsbereich, sowie den tatsächlichen Fehler 1. Art. Skizziere grob die Verteilungsfunktion und kennzeichne die markanten Stellen. Das Signifikanzniveau soll höchstens 5% betragen.
2. Ausführliche Lösung
Aufgabenanalyse und aufstellen der Hypothesen
Man möchte überprüfen, ob die Beliebtheit der Schule zugenommen hat, ob also die Vermutung p > 0,37 zutrifft.
Bei der Aufstellung der Hypothesen geht man so vor:
Was gezeigt werden soll, bildet die Alternativhypothese, das Gegenteil davon die Nullhypothese.
Nullhypothese H0: p ≤ 0,37; Alternativhypothese H1: p > 0,37.
Bei Ablehnung der Nullhypothese nimmt man die Alternativhypothese an.
H0 will man mit die Umfrage testen.
Das Signifikanzniveau soll höchstens 5% betragen.
Auf dieser Grundlage wird für H0 ein Annahmebereich und ein Ablehnungsbereich festgelegt. Da große Werte gegen H0 sprechen, handelt es sich um einen rechtsseitigen Test.

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50
Auswertung:
Der Annahmebereich von H0 beinhaltet 0 bis 85 positive Elternmeinungen.
Der Ablehnungsbereich von H0 beinhaltet 86 bis 200 positive Elternmeinungen.Würde bei der Umfrage herauskommen, dass mehr als 85 positive Elternentscheidungen vorliegen, dann fiele das in den Ablehnungsbereich von H0. Folglich müsste man die Nullhypothese ablehnen. Die Alternativhypothese H1: p > 0,37 würde man annehmen. Die Schule scheint attraktiver geworden zu sein. Der Fehler, den man bei dieser Entscheidung gemacht hätte, beträgt 4,65%. Das bedeutet, mit einer Wahrscheinlichkeit von 4,65% würde man die Hypothese H0 zu unrecht ablehnen.
Käme bei der Umfrage heraus, dass höchstens 85 positive Elternmeinungen vorlägen, dann würde man die Hypothese H0 annehmen. In diesem Fall könnte man nicht behaupten, die Schule sei attraktiver geworden.
3.
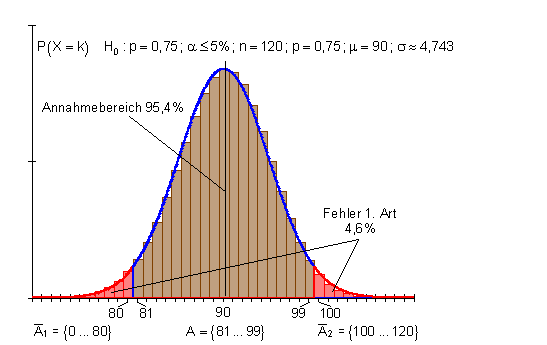
Im vergangenen Jahr wechselten 75% aller Grundschüler eines Schulbezirkes nach der 4. Klasse zur Realschule. Das Schulamt vermutet, dass der Anteil der Schüler, die zur Realschule wechseln auch in diesem Jahr unverändert bleibt. Diese Annahme soll durch eine Befragung von 120 Eltern überprüft werden.
a) Wie lautet die Entscheidungsregel für α ≤ 5%?
Berechne und beschreibe den Fehler 1. Art!
Skizziere grob die Verteilungsfunktion und kennzeichne die markanten Stellen.
b) Beschreibe und berechne den Fehler 2. Art, wenn dem Zufallsversuch tatsächlich eine Erfolgswahrscheinlichkeit von p = 0,7 zugrunde liegt. Skizziere grob die Verteilungsfunktion und kennzeichne die markanten Stellen.
3. Ausführliche Lösungen
a) Aufgabenanalyse und aufstellen der Hypothesen.
Es soll überprüft werden, ob der Anteil der Grundschüler, der zur Realschule wechselt, wie im vergangenen Jahr 75% beträgt. Da weder eine eindeutige Abweichung nach oben oder nach unten vermutet wird, handelt es sich um einen zweiseitigen Hypothesentest.
Die Hypothesen lauten:
Nullhypothese: H0: p = 0,75; Alternativhypothese H1: p ≠ 0,75.
Der Ablehnungsbereich, bestimmt durch das Signifikanzniveau von 5%, verteilt sich gleichmäßig auf beide Seiten.

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50
Auswertung:
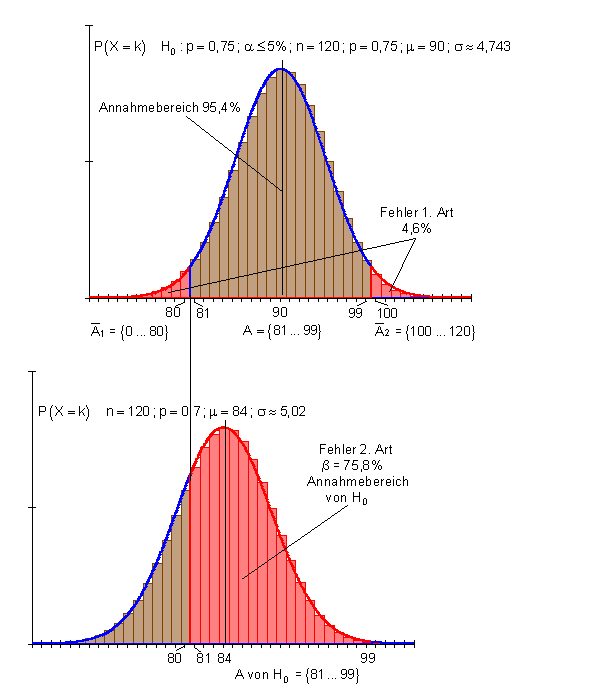
Der Annahmebereich von H0 beinhaltet 81 bis 99 Entscheidungen für die Realschule.
Der Ablehnungsbereich von H0 beinhaltet 0 bis 80, bzw. 100 bis 120 Entscheidungen für die Realschule.Falls p = 0,75 richtig ist, aber das Stichprobenergebnis zufällig in den Ablehnungsbereich fällt, lehnt man fälschlicherweise H0 ab. Die Wahrscheinlichkeit für den Fehler 1. Art ist gleich der Wahrscheinlichkeit für den Ablehnungsbereich.
1 – 0,954 = 0,046 (4,6%).
b) Aufgabenanalyse
Falls H0 nicht gilt, sondern p = 0,7 richtig ist, d.h. die Hypothese p = 0,75 ist falsch, aber das Stichprobenergebnis fällt zufällig im Annahmebereich von H0 , nimmt man H0 fälschlicherweise an. Die Wahrscheinlichkeit dafür, diesen Fehler zu machen ist der Fehler 2. Art.
Man berechnet diesen Fehler, indem man unter der Annahme, dass p = 0,7 richtig ist, die Wahrscheinlichkeit des Annahmebereichs von H0 bestimmt.
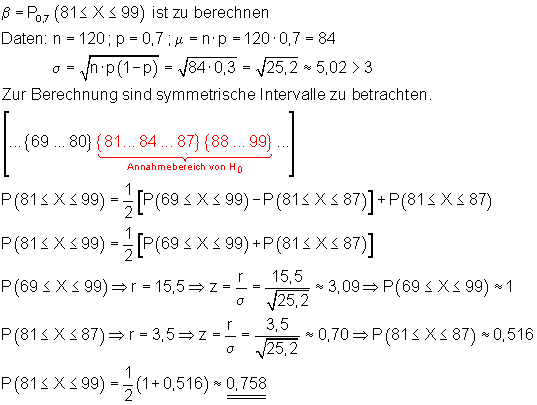
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50
Auswertung:
Falls H0 falsch und p = 0,7 richtig ist, fällt das Ergebnis dennoch zu 75,8% in den Annahmebereich von H0.
Die Nullhypothese würde fälschlicherweise angenommen werden. Dieser Fehler heißt Fehler 2. Art. Er beträgt 75,8% und ist im Vergleich zum Fehler 1. Art mit 4,6% sehr groß.
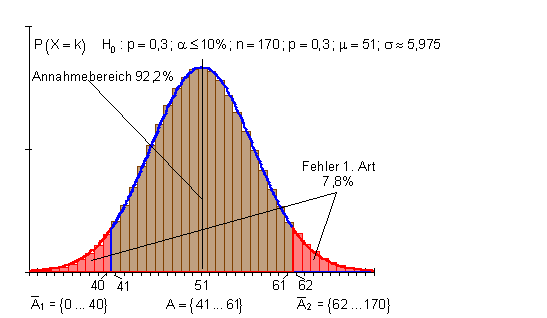
4.
Der Hersteller eines Glücksspielautomaten behauptet, das die Wahrscheinlichkeit für eine bestimmte Gewinnkombination p = 0,3 beträgt. In 170 Spielrunden soll diese Angabe überprüft werden.
a) Gib eine Entscheidungsregel für das Signifikanzniveau α ≤ 10% an und berechne den Fehler 1. Art!
Skizziere grob die Verteilungsfunktion und markiere die markanten Werte.
Bemerkung: Der Annahmebereich soll symmetrisch zum Erwartungswert liegen.
b) Bestimme die Wahrscheinlichkeit für den Fehler 2. Art, falls die tatsächliche Wahrscheinlichkeit dieser Gewinnkombination nur p = 0,2 beträgt. Skizziere grob die Verteilungsfunktion und markiere die markanten Werte.
4. Ausführliche Lösungen
a) Aufgabenanalyse und aufstellen der Hypothesen
Es soll überprüft werden, ob eine bestimmte Gewinnkombination mit der Wahrscheinlichkeit von p = 0,3 auftritt. Da weder eine eindeutige Abweichung nach oben oder nach unten vermutet wird, handelt es sich um einen zweiseitigen Hypothesentest.
Die Hypothesen lauten:
Nullhypothese: H0: p = 0,3; Alternativhypothese H1: p ≠ 0,3.
Der Ablehnungsbereich, bestimmt durch das Signifikanzniveau von 10%, verteilt sich gleichmäßig auf beide Seiten.

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50
Auswertung:
Falls p = 0,3 richtig ist, aber das Stichprobenergebnis zufällig in den Ablehnungsbereich fällt, geht man fälschlicherweise davon aus, dass H0 abgelehnt werden muss. Die Wahrscheinlichkeit für den Fehler 1. Art ist gleich der Wahrscheinlichkeit für den Ablehnungsbereich,
also 1 – 0,922 = 0,078 (7,8%).

b) Aufgabenanalyse
Falls H0 nicht gilt, sondern p = 0,2 richtig ist, d.h. die Hypothese p = 0,3 ist falsch, aber das Stichprobenergebnis fällt zufällig im Annahmebereich von H0 , nimmt man H0 fälschlicherweise an. Die Wahrscheinlichkeit dafür, diesen Fehler zu machen ist der Fehler 2. Art. Man berechnet diesen Fehler, indem man unter der Annahme, dass p = 0,2 richtig ist, die Wahrscheinlichkeit des Annahmebereichs von H0 bestimmt.
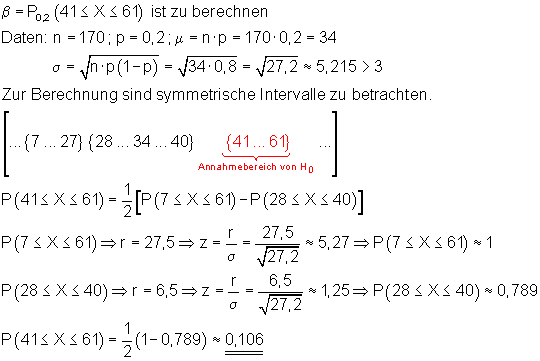
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50
Auswertung:
Falls H0 falsch und p = 0,2 richtig ist, fällt das Ergebnis dennoch zu 10,6% in den Annahmebereich von H0. Die Nullhypothese würde fälschlicherweise angenommen werden. Dieser Fehler heißt Fehler 2. Art. Er beträgt 10,6% und ist im Vergleich zum Fehler 1. Art mit 7,8% geringfügig größer. 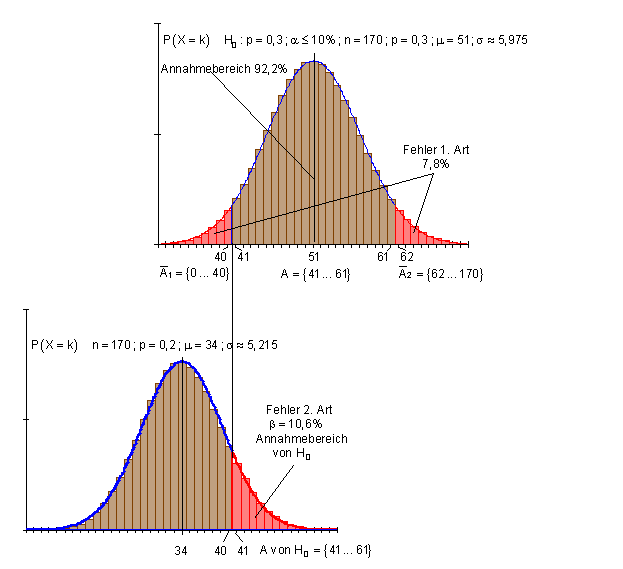
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu: Grundlagen zum Hypothesentest.
und hier der Hypothesentest, ein einfacher Zugang mit Würfeln.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung.

