Hier findest du die Lösungen zu weiteren Aufgaben mir Exponentialgleichungen, diesmal geht es um gebrochene Exponenten.
1. Berechne!
Ausführliche Lösungen
a)
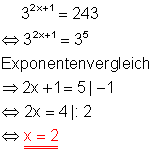
Da 243 eine Potenz der Zahl 3 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
b)
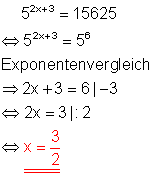
Da 15625 eine Potenz der Zahl 5 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
c)
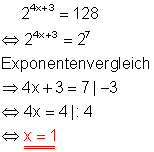
Da 128 eine Potenz der Zahl 2 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
d)
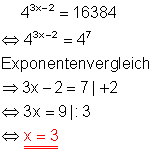
Da 16384 eine Potenz der Zahl 4 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
e)

Da 1296 eine Potenz der Zahl 6 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
f)
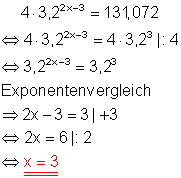
Da 131,072 das 4-fache einer Potenz der Zahl 3,2 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
2. Berechne!
Ausführliche Lösungen
a)
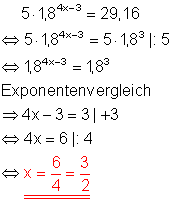
Da 29,16 das 5-fache einer Potenz der Zahl 1,8 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
b)

Da 450 das 8-fache einer Potenz der Zahl 7,5 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
c)
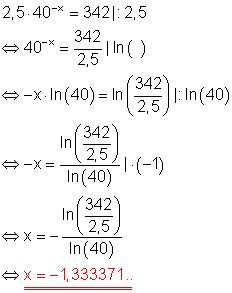
d)
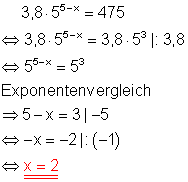
Da 475 das 3,8-fache einer Potenz der Zahl 5 ist, lässt sich die Exponentialgleichung durch Exponentenvergleich lösen.
e)
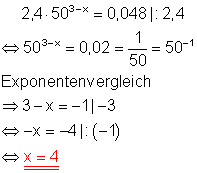
Da 0,02 eine Potenz der Zahl 50 ist, lässt sich die Exponentialgleichung auf einfache Weise durch Exponentenvergleich lösen.
f)
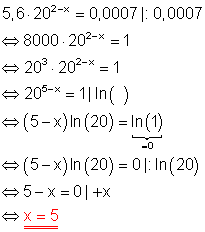
3. Berechne!
Ausführliche Lösungen
a)
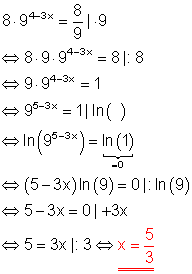
b)
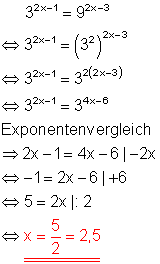
c)

d)
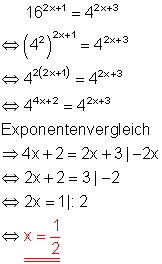
e)

f)
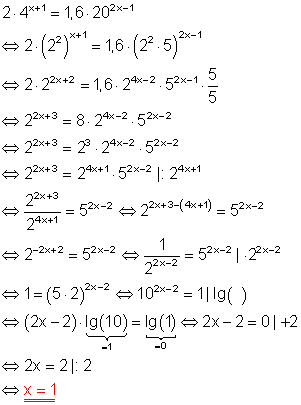
4. Berechne!
Ausführliche Lösungen
a)

b)

c)
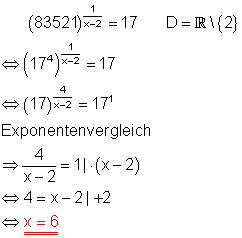
d)

e)
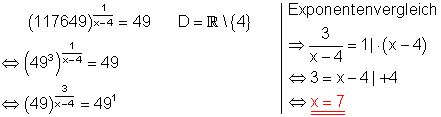
f)
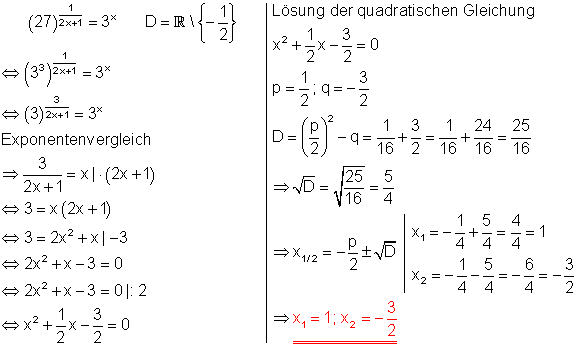
5. Berechne!
Ausführliche Lösungen
a)
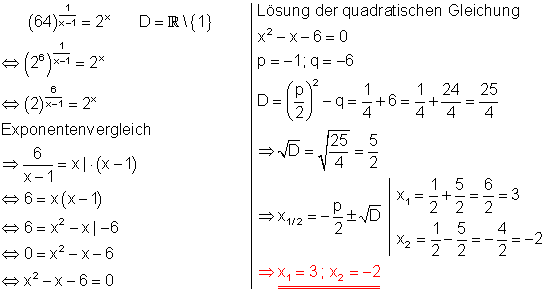
b)
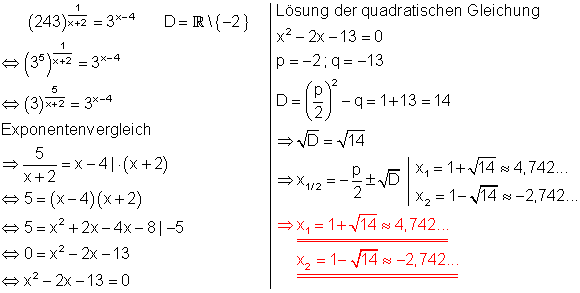
c)
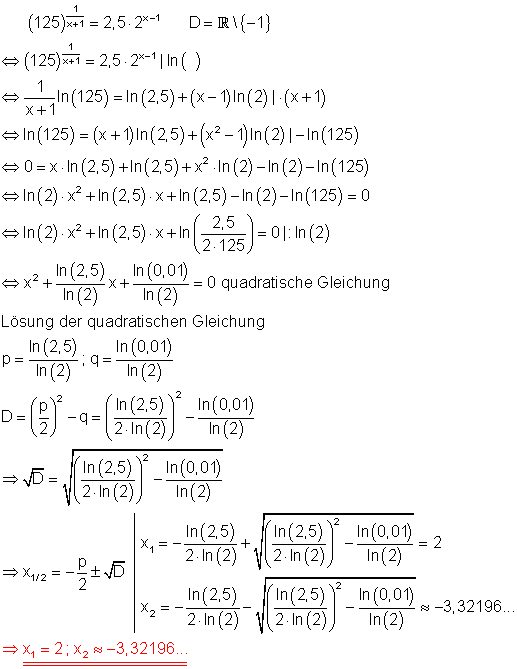
d)
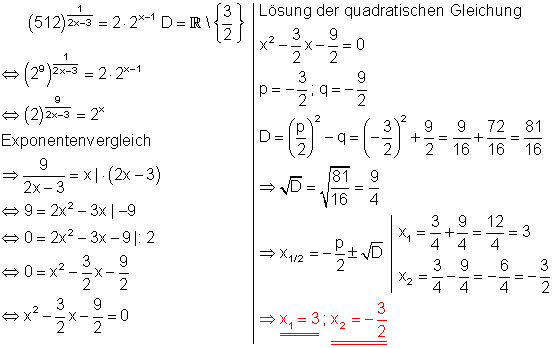
e)
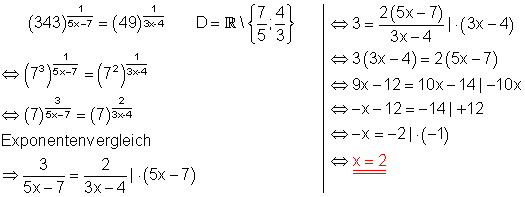
f)

6. Berechne!
Ausführliche Lösungen
a)

b)
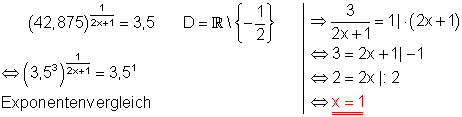
c)
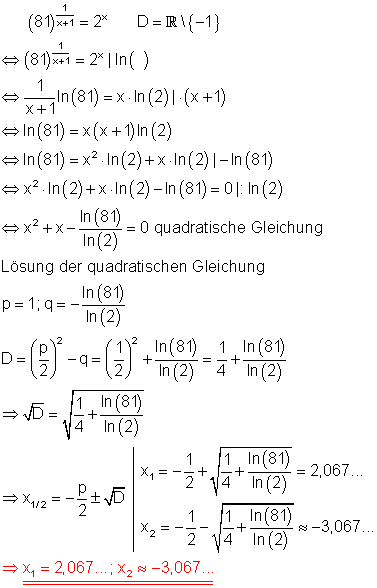
7. Berechne!
Ausführliche Lösungen
a)
4 \cdot 5^{2x-3} = 5 \cdot 10^{x-1} \Leftrightarrow 2^2 \cdot 5^{2x-3} = 5^1 \cdot (2 \cdot 5)^{x-1} \\ \Leftrightarrow 2^2 \cdot 5^{2x-3} = 5^1 \cdot 2^{x-1} \cdot 5^{x-1} \\ \Leftrightarrow 2^2 \cdot 5^{2x-3} = 2^{x-1} \cdot 5^x \, \big \vert : 5^x \\ \Leftrightarrow 2^2 \cdot 5^{x-3} = 2^{x-1} \, \big \vert : 2^2 \\ \Leftrightarrow 5^{x-3} = 2^{x-3} \, \big \vert : 2^{x-3} \\ \Leftrightarrow (\frac{5}{2})^{x-3} = 1 \, \big \vert \ln( \, ) \\ \Leftrightarrow (x-3) \underbrace{ \ln( \frac{5}{2}}_{\neq 0} = \underbrace{ \ln(1)}_{= 0} \, \big \vert : \ln(\frac{5}{2}) \\ \Leftrightarrow x-3 = 0 \, \big \vert +3 \Leftrightarrow \textcolor{red}{\underline{\underline{x = 3}}}
b)
2^{2(x+1)} - 2^{x+3} = 2^{x+5} - 2^{2x+4} \Leftrightarrow 2^{2x+3} - 2^{x+3} = 2^{x+5} - 2^{2x+4} \, \big \vert 2^2 \, ausklammern \\ \Leftrightarrow \cancel{2^2} ( 2^{2x} - 2^{x+1}) = \cancel{2^2} (2^{x+3} - 2^{2x+2}) \, \big \vert 2^x \, ausklammern \\ \Leftrightarrow 2^x(2^x - 2^1) = 2^x(2^3 - 2^{x+2}) \, \big \vert : 2^x \\ \Leftrightarrow 2^x - 2 = 2^3 - 2^{x+2} \big \vert +2 \\ \Leftrightarrow 2^x = 8 + 2 - 2^{x+2} \, \big \vert +2^{x+2} \\ \Leftrightarrow 2^x + 2^{x+2} = 10 \\ \Leftrightarrow 2^x + 2^x \cdot 4 = 10 \\ \Leftrightarrow 2^x(1 + 4) = 10 \, \big \vert : 5 \\ \Leftrightarrow 2^x = 2^1 \\ Exponentenvergleich \\ \Leftrightarrow \textcolor{red}{\underline{\underline{x = 1}}}
c)
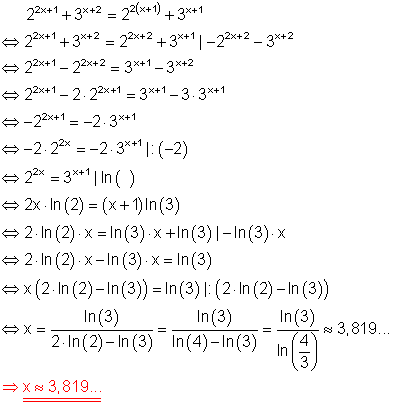
d)
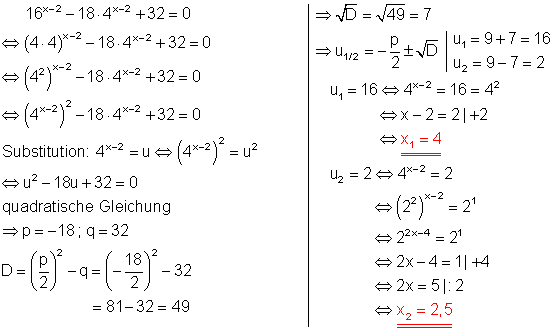
8. Berechne!
Ausführliche Lösungen
a)
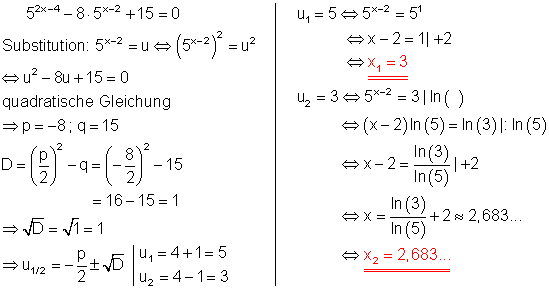
b)

c)
2^{5x+1}+3^{2x+2} = 2^{5x+1}+3^{x+4} \ nach \ den \ Basen \ anordnen
\Leftrightarrow 2^{5x+2}-2^{5x+1} = 3^{2x+4}-3^{2x+2} \\ \Leftrightarrow 2^2\cdot2^{5x}-2^1\cdot2^{5x} = 3^4\cdot3^{2x}-3^2\cdot3^{2x} \\ \Leftrightarrow 2^{5x}(2^2-2^1) = 3^{2x}(3^4-3^2) \\ \Leftrightarrow 2^{5x}\cdot2 = 3^{2x}\cdot72 \ | \ \div2 \\ \Leftrightarrow 2^{5x} = 36\cdot3^{2x} \ | \ \ln() \\ \Leftrightarrow 5x\cdot\ln(2) = \ln(36)+2x\cdot\ln(3) \ | \ -2x\cdot\ln(3) \\ \Leftrightarrow 5x\cdot\ln(2)-2x\cdot\ln(3) = \ln(36) \\ \Leftrightarrow x(5\cdot\ln(2)-2x\cdot\ln(3)) = \ln(36) \ | \ \div(5\cdot\ln(2)-2\cdot\ln(3)) \\ \Leftrightarrow x = \frac{\ln(36)}{5\cdot\ln(2)-2\cdot\ln(3)} = \frac{\ln(36)}{\ln(2^5)-\ln(3^2)} = \frac{\ln(36)}{\ln(\frac{2^5}{3^2})} = \frac{\ln(36)}{\ln(\frac{32}{9})} \approx2,825\dots \\ \Rightarrow \underline{\underline{x \approx 2,825\dots}}
d)
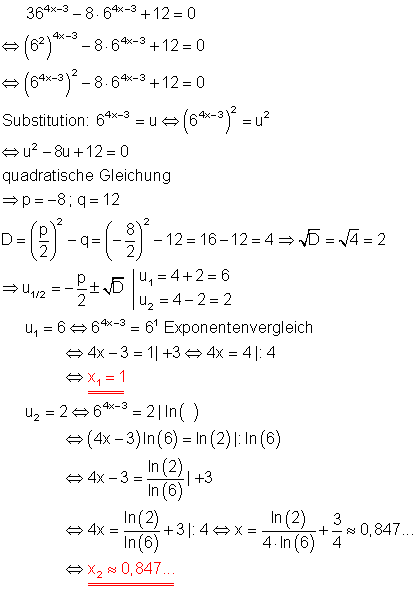
Hier findest du die Aufgaben hierzu.
Und hier die Theorie: Exponentialgleichungen.
Eine große Hilfe bieten die Regeln zum Lösen von Exponentialgleichungen.
Hier eine Übersicht über weitere Beiträge zu Gleichungen, darin auch Links zu weiteren Aufgaben.

