Hier findest du die Lösungen der einfachen Aufgaben zu Polynomgleichungen I.
Dabei kann dir sicher eines dieser Videos helfen: Playlist aller Videos zu Polynomgleichungen.
1. a) Löse die Gleichungen nach x auf und mache die Probe!
Ausführliche Lösung
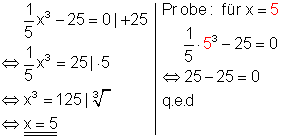
Es sei n >1 eine natürliche Zahl. Ist a eine nichtnegative reelle Zahl, so besitzt die Gleichung xn = a genau eine nichtnegative Lösung. Diese wird als n-te Wurzel aus a bezeichnet. Bei der Probe geht man erst mal davon aus, dass die Gleichung stimmt. Führt die Rechnung auf keinen Widerspruch, so ist der eingesetzte Lösungswert richtig.
q. e. d. steht für: quod erat demonstrandum, lateinisch für: was zu beweisen war.
1. b) Löse die Gleichungen nach x auf und mache die Probe! Ausführliche Lösung
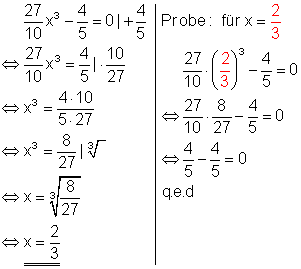
Die Multiplikation einer Gleichung mit dem Kehrwert eines Bruches ist äquivalent zur Division durch diesen Bruch. Die Multiplikation mit dem Kehrwert ist oft einfacher durchzuführen.
1. c)
Löse die Gleichungen nach x auf und mache die Probe!
Ausführliche Lösung:
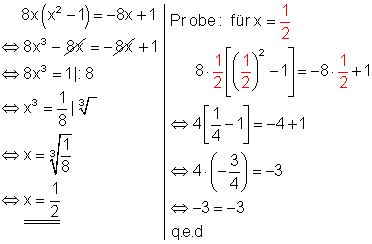
Wenn auf beiden Seiten einer Gleichung, die nur aus Summanden besteht, gleiche Summanden auftreten, kann man diese einfach streichen.
2. a) Löse die Gleichungen nach x auf und mache die Probe!
Ausführliche Lösung
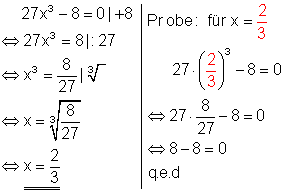
2. b)
Löse die Gleichungen nach x auf und die Probe!
Ausführliche Lösung
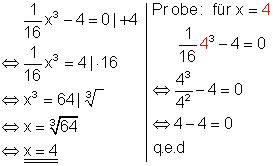
2. c)
Löse die Gleichungen nach x auf und mache die Probe!
Ausführliche Lösung
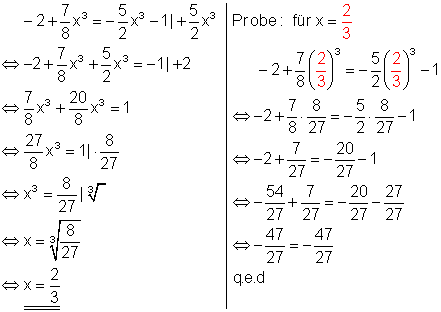
3. a) Löse die Gleichungen nach x auf und mache die Probe!
Ausführliche Lösung
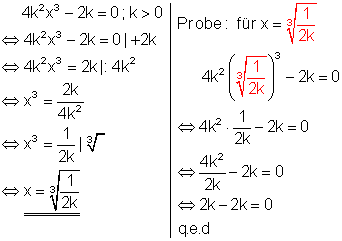
Die Vorgabe von k > 0 verhindert, das der Nenner des Bruches unter der Wurzel 0 wird. Eine Division durch 0 ist nicht erlaubt.
3. b)
Löse die Gleichungen nach x auf und machee die Probe!
Ausführliche Lösung
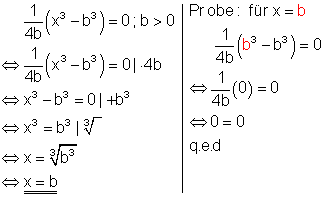
3. c)
Löse die Gleichungen nach x auf und mache die Probe!
Ausführliche Lösung
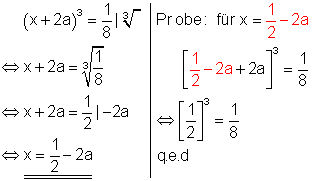
4. Löse die Gleichungen nach x auf!
Gibt es für jede Wahl von k eine Lösung? Begründen Sie Ihre Aussage.
Ausführliche Lösung
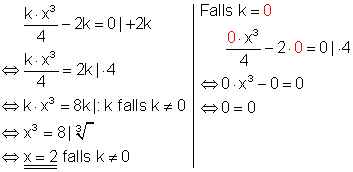
Die Lösung x = 2 gilt nur für den Fall, dass k ungleich Null ist. Denn durch Null darf man nicht teilen. Setzt man hingegen für k den Wert 0 in die Ausgangsgleichung ein, dann ist die Lösung für alle x-Werte Null. Man sagt auch, die Gleichung hat für k = 0 unendlich viele Lösungen.
5. Bestimmte Bakterien verdreifachen ihre Zahl innerhalb von 4 Stunden.
Wie groß ist die prozentuale Vermehrung in einer Stunde?
Ausführliche Lösung
Vorbemerkung:
Die Wachstumsfunktion für exponentielles Wachstum lautet:
![]()
Dabei ist:
N0 der Anfangswert
t die Zeit (Sekunden, Minuten, Stunden …)
q die Änderungsrate
Eine Wachstumsfunktion beschreibt, wie sich der Bestand einer Menge (z.B. Bakterien, Zinsen, Bevölkerung) im Laufe der Zeit verändert.
Exponentiell bedeutet, dass die Veränderung pro Zeiteinheit nicht konstant ist, sondern prozentual zum vorherigen Wert des Bestandes.
Die Änderungsrate q enthält also die prozentuale Vermehrung.
Ist q > 1, so spricht man von einem Wachstum.
Ist q < 1, so spricht man von einer Abnahme.
Für die gestellte Aufgabe bedeutet das:
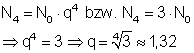
Die Änderungsrate beträgt etwa q = 1,32.
Das bedeutet, dass die prozentuale Vermehrung der Bakterien pro Stunde etwa 32% beträgt.
6. Zu Beginn eines Jahres wird der Zeitwert eines Autos neu festgelegt.
Für einen 5 Jahre alten Gebrauchtwagen bietet ein Händler 8500 €.
Wie hoch war der jährliche Wertverlust (in Prozent vom Zeitwert), wenn man davon ausgeht, dass dieser in den ersten 5 Jahren gleich hoch ist?
Ausführliche Lösung
Vorbemerkung:
Es handelt sich bei dem jährlichen Wertverlust um eine Abnahme.
Für die Aufgabe bedeutet das:
W5 = W0q5 wobei q die jährliche Änderungsrate ist.
Wenn diese z.B. q = 0,8 betragen würde, dann wäre das Auto nach einem Jahr nur noch 80% vom Neupreis wert.
Der Wertverlust wäre dann 100% – 80% = 20%.
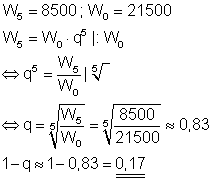
Der Wertverlust pro Jahr beträgt etwa 17%.
7. a) Löse die Gleichungen nach x auf!
Ausführliche Lösung
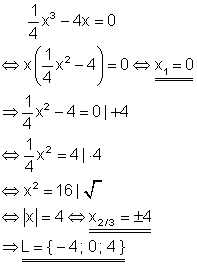
Aus der Linken Seite der Gleichung kann x ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden, der da lautet:
„Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.“
Die Lösung der Gleichung findet man also dadurch, dass man jeden Faktor für sich gleich Null setzt.
7. b)
Löse die Gleichungen nach x auf! Ausführliche Lösung
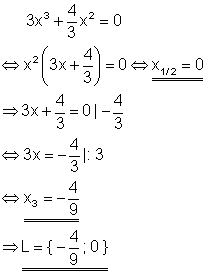
Lösung nach dem Satz vom Nullprodukt.
7. c)
Löse die Gleichungen nach x auf! Ausführliche Lösung
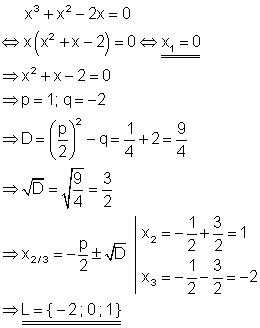
Der zweite Faktor vom Nullprodukt ist eine quadratische Gleichung. Diese lässt sich z.B. mit der p-q-Formel lösen.
8. a) Löse die Gleichung!
Ausführliche Lösung
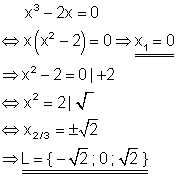
Lösung nach dem Satz vom Nullprodukt.
8. b)
Löse die Gleichung!
Ausführliche Lösung
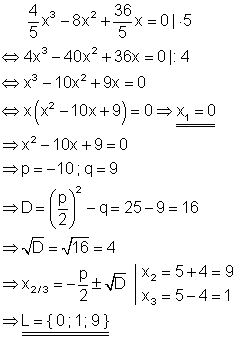
8. c)
Löse die Gleichung!
Ausführliche Lösung
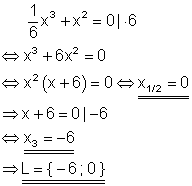
9. a) Löse die Gleichung!
Ausführliche Lösung
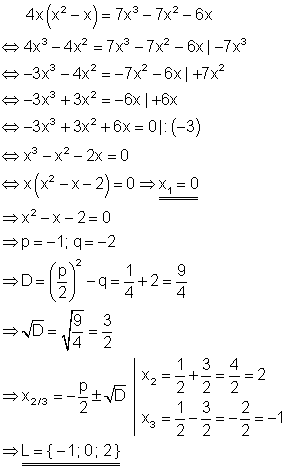
9. b) Löse die Gleichung! Ausführliche Lösung
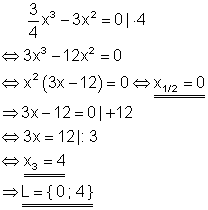
9. c) Löse die Gleichung! Ausführliche Lösung
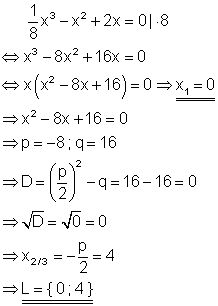
10. Bestimme die Anzahl der Lösungen in Abhängigkeit von a!
Ausführliche Lösung
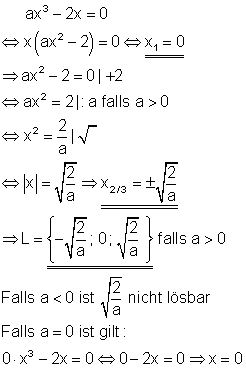
1. Falls a > 0 ist, gibt es 3 Lösungen:
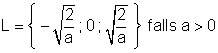
2. Falls a = 0 ist, gibt es nur eine Lösung: L = { 0 }.
3. Falls a < 0 ist, gibt es nur eine Lösung: L = { 0 }, da die Wurzel nicht lösbar ist.
11. Bestimme die Anzahl der Lösungen in Abhängigkeit von c!
Ausführliche Lösung

Die Lösung x1 = 0 existiert für jeden Wert von c.
Falls c
= -1/4 existieren zwei Lösungen.
> -1/4 existieren drei Lösungen.
< -1/4 existiert nur die Lösung x1 = 0.
12. Welcher Zusammenhang besteht zwischen b und c, wenn folgende Gleichung genau zwei Lösungen hat?
Ausführliche Lösung
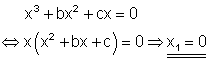
Genau zwei Lösungen bedeutet, dass die quadratische Gleichung x2 + bx + c = 0 nur eine Lösung haben darf.
Das ist aber nur dann der Fall, wenn die Diskriminante D = 0 ist.
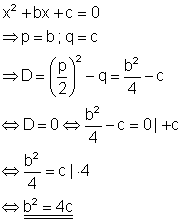
b2 =4c ist der Zusammenhang zwischen b und c falls die Gleichung genau zwei Lösungen hat.
Hier findest du die Aufgaben
und hier die Theorie Polynomgleichungen
hier weitere Aufgaben Polynomgleichungen VII.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

