Hier findest du die Lösungen der Aufgaben zu quadratischen Gleichungen V mit Brüchen mit komplettem Lösungsweg.
Dabei können dir diese Videos helfen: Playlist aller Videos zu quadratischen Gleichungen .
1. Berechne
Ausführliche Lösungen:
a)
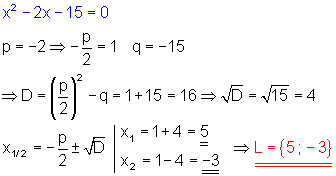
b)
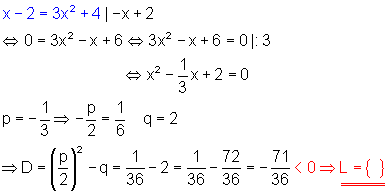
c)
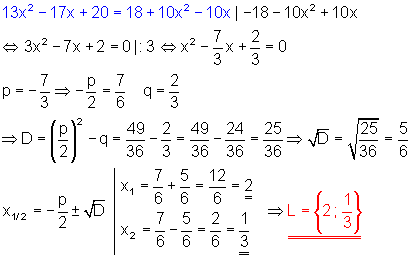
2. Nimm Stellung
Ausführliche Lösung:
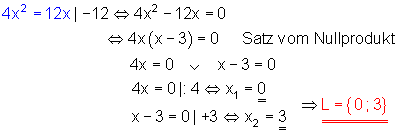
Division durch x ist nur erlaubt für x ungleich Null. Denn durch Null darf man nicht dividieren.
3. Bestimme
Ausführliche Lösungen:
a) Berechne die Lösungsmenge für a = 0 und für a ungleich Null!
katex is not defined
katex is not defined
katex is not defined Nach dem Satz vom Nullprodukt gilt:
katex is not defined
b) Berechne die Lösungsmenge in Abhängigkeit von a!
katex is not defined
katex is not defined
katex is not defined
Fall 1: katex is not defined \\
katex is not defined
Fall 2: katex is not defined
Deshalb wenden wir den Satz vom Nullprodukt an.
katex is not defined
4. Berechne
Ausführliche Lösungen:
a)
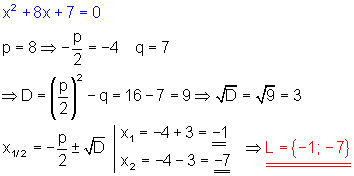
b)
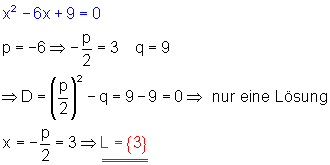
c)
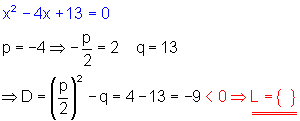
d)
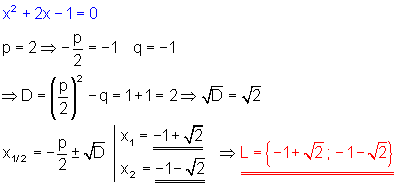
e)
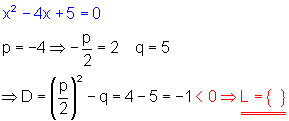
f)Zu beachten ist die Definitionsmenge: x darf nicht -2 sein.
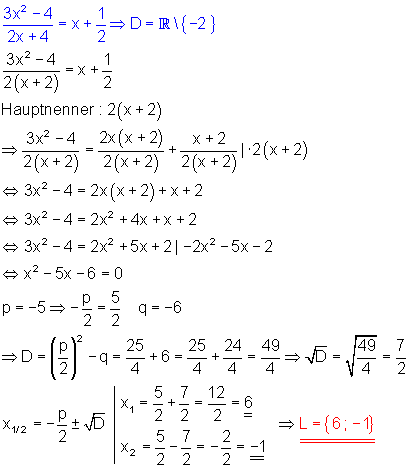
5. Lösungsmenge
Ausführliche Lösungen:
a) Zu beachten ist die Definitionsmenge: x darf nicht Null sein.
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
b) Zu beachten ist die Definitionsmenge: x darf nicht -3 sein.
katex is not defined
katex is not defined
katex is not defined
Als nächstes klammern wir x aus:
katex is not defined
Dann wenden wir den Satz vom Nullprodukt an:
katex is not defined
c) Zu beachten ist die Definitionsmenge: x darf nicht Null sein.
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
d) Zu beachten ist die Definitionsmenge: x darf nicht Null sein.
katex is not defined
katex is not defined
katex is not defined
katex is not defined
e) Zu beachten ist die Definitionsmenge: x darf nicht Null sein.
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
f) Zu beachten ist die Definitionsmenge: x darf nicht Null, nicht 2 und auch nicht -1 sein.
katex is not defined
Der Hauptnenner ist: katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
6. Definitionsmenge
Ausführliche Lösungen:
a) Zu beachten ist die Definitionsmenge: x darf nicht 4/3 und auch nicht -1/4 sein.
katex is not defined
Als erstes bestimmen wir die Definitionsmenge:
katex is not defined
katex is not defined
Der Hauptnennen ist deshalb: katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
Da die Diskriminante kleiner als Null ist, hat die quadratische Gleichung keine Lösung. Das bedeutet, die Bruchgleichung hat ebenfalls keine Lösung.
b) Zu beachten ist die Definitionsmenge: x darf nicht 1 sein.
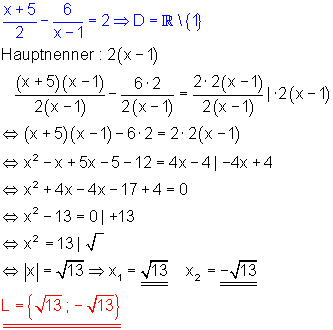
c) Zu beachten ist die Definitionsmenge: a darf nicht Null sein.
Statt x ist a die Variable nach der die quadratische Gleichung aufzulösen ist.
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
katex is not defined
d) Zu beachten ist die Definitionsmenge: x darf nicht Null und auch nicht 4 sein.
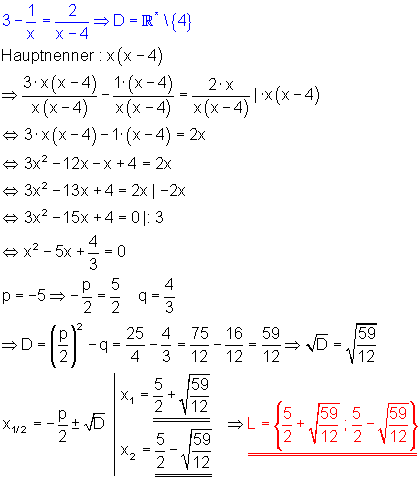
e) Zu beachten ist die Definitionsmenge: x darf nicht Null und auch nicht 2 sein.
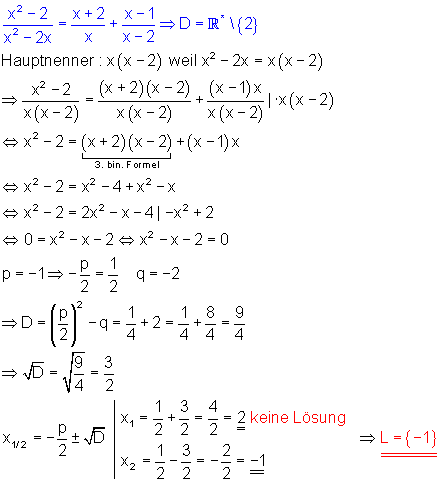
Der formal berechnete Wert x = 2 ist keine Lösung der Bruchgleichung, da 2 nicht zur Definitionsmenge gehört.
f) Zu beachten ist die Definitionsmenge: x darf nicht 1 und auch nicht 9 sein.
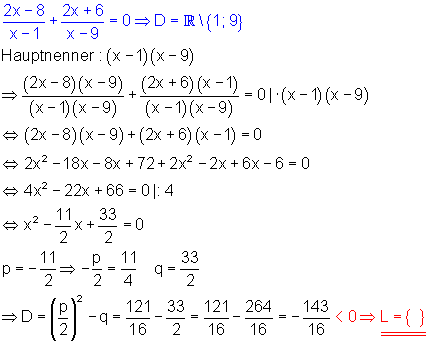
Da die Diskriminante kleiner als Null ist, hat die quadratische Gleichung keine Lösung.
Das bedeutet, die Bruchgleichung hat ebenfalls keine Lösung.
7. Definitionsmenge
Ausführliche Lösungen
a) Zu beachten ist die Definitionsmenge: x darf nicht 1 und auch nicht 9 sein.
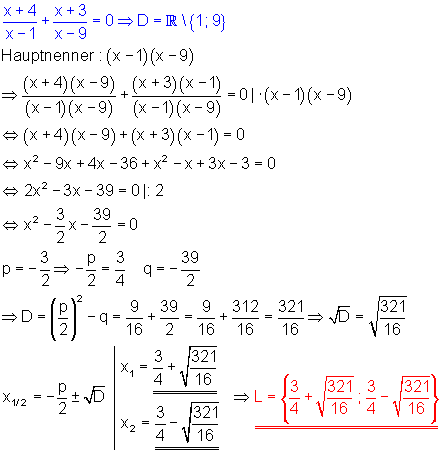
b) Zu beachten ist die Definitionsmenge: x darf nicht Null sein.
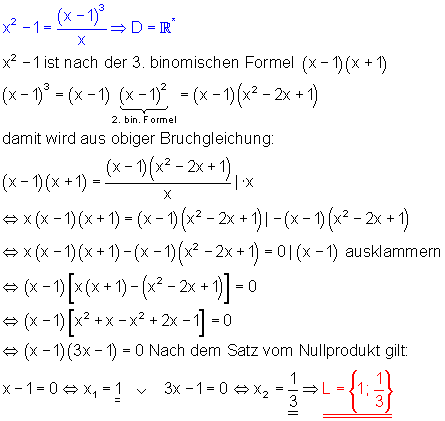
c) Zu beachten ist die Definitionsmenge: v darf nicht 2 sein.
Statt x ist v die Variable nach der die quadratische Gleichung aufzulösen ist.
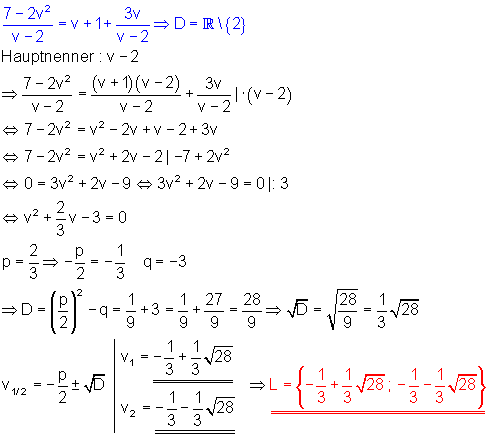
d) Zu beachten ist die Definitionsmenge: m darf nicht Null und auch nicht -1 sein.
Statt x ist m die Variable nach der die quadratische Gleichung aufzulösen ist.
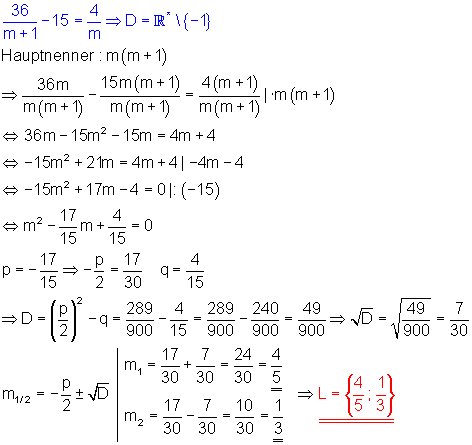
e) Zu beachten ist die Definitionsmenge: a darf nicht 3 und auch nicht 1 sein.
Statt x ist a die Variable nach der die quadratische Gleichung aufzulösen ist.
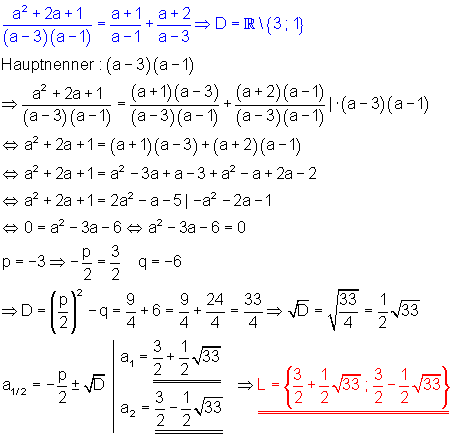
f) Zu beachten ist die Definitionsmenge: x darf nicht 2 sein.
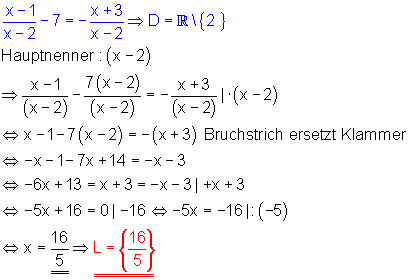
Die Äquivalenzumformung der Bruchgleichung führt auf eine lineare Gleichung. Diese hat nur eine Lösung.
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie hier: Quadratische Gleichungen und p-q-Formel
und Zusammenfassung Quadratische Funktionen.
Hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zur Theorie und zu weiteren Aufgaben.
