Hier findest du die Lösungen der Aufgaben zur Differentialrechnung VII aus der Praxis, insbesondere Kostenrechnung.
Dazu kannst du dir das 📽️ Video Kostenfunktion aufstellen ansehen.
Die Gesamtkosten eines Betriebes
werden bei einer maximalen Ausbringungsmenge von 10 Mengeneinheiten (ME) beschrieben durch K(x). Der Verkaufspreis pro ME beträgt 28 GE. K(x) = x3 – 12 x2 + 50x + 40.
a)
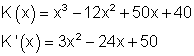
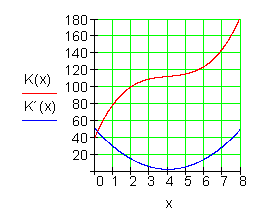
Der Graph der Grenzkostenfunktion ist eine nach oben geöffnete Parabel.
Im Scheitelpunkt dieser sind die Grenzkosten am geringsten.
1. b)

1. c)

1. d)

1. e)
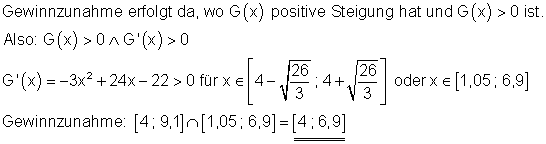
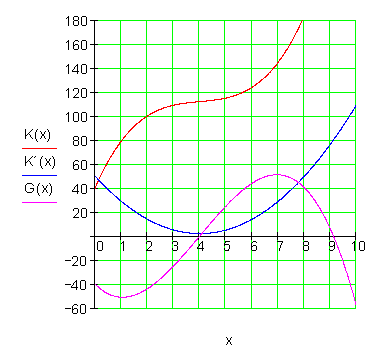
Die Graphen:
2. Gegeben ist das Weg-Zeit-Diagramm s(t) eines bewegten Körpers.
a)
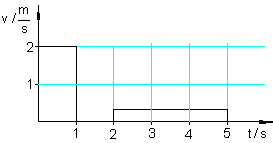
Von 0 bis 1 s :
Bewegung mit gleichbleibender Geschwindigkeit v = 2 m/s
Von 1 bis 2 s:
Stillstand v = 0 m/s
Von 2 bis 5 s:
Bewegung mit gleichbleibender Geschwindigkeit v = 1/3 m/s
2. b)
3. Die Abbildung zeigt den Verlauf einer Bewegung im Weg- Zeit- Diagramm.
a)
Ein Gegenstand wird senkrecht nach oben geworfen.Für t > 3 ist s < 0, d.h. der Gegenstand befindet sich unterhalb der Abwurfstelle.
3. b)

3. c)
![]()
Die Geschwindigkeit ist am Anfang positiv, d.h. der Körper bewegt sich nach oben.
Sie nimmt aber ab und ist bei t = 1,5 s null.
Der Körper hat da seine größte Höhe erreicht.
Dann ist die Geschwindigkeit negativ, der Körper fällt, er bewegt sich wieder nach unten.
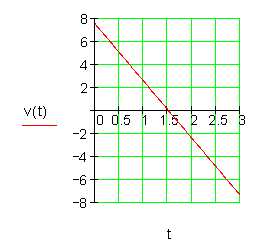
4. Gegeben ist der Geschwindigkeitsverlauf einer Bewegung.
0 – 100 m: Die Geschwindigkeit nimmt zu.
100 – 150 m: Die Geschwindigkeit bleibt gleich: 40 km/h.
150 – 200 m: Die Geschwindigkeit nimmt ab.
250 – 300 m: Die Geschwindigkeit bleibt gleich: 15 km/h.
300 – 400 m: Die Geschwindigkeit nimmt zu.
ab 400 m: Die Geschwindigkeit bleibt konstant 40 km/h.
Erklärung:
Auf einer abfallenden Straße wird beschleunigt, die folgende Straße ist eben. Anschließend geht es steil bergauf, die Geschwindigkeit verringert sich bis auf 15 km/h. Danach folgt eine Talfahrt, bei der wieder Geschwindigkeit gewonnen wird, die Höchstgeschwindigkeit von 40 km/h kann danach gehalten werden auf der folgenden leicht abschüssigen Strecke.
Hier findest du die Aufgaben zur Differentialrechnung VIII
und hier die Theorie: Differentialrechnung Anwendungen aus Betriebswirtschaft und Naturwissenschaften
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.

