Hier findest du die Aufgaben zu lineare Funktionen V, darin geht es darum, ob drei Geraden durch einen Punkt verlaufen.
1. Prüfe ob die Geraden g, h, i durch einen Punkt verlaufen!
a) g(x) = x + 1
h: 2y + x + 4 = 0
i: 3y – 5x = 7
b) ![]()
2. Wertetabelle
Gegeben ist eine Wertetabelle für zwei lineare Funktionen f(x) und g(x).
Wo schneiden sich die Graphen beider Funktionen?
In welchem Quadranten liegt der Schnittpunkt?
Für welche x -Werte gilt f(x) < g(x)?
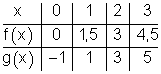
3. Bestimme den Schnittpunkt
beider Geraden und zeichne die Graphen in ein Koordinatensystem!
f(x) = 0,04x + 20
g(x) = 0,15x + 15
4. Betrachte das Schaubild mit den 4 Graphen.
a) Bestimme alle Funktionsgleichungen!
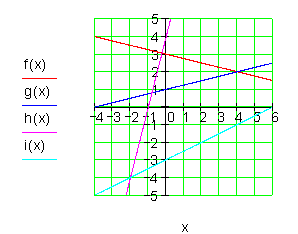
b) Berechne die Schnittpunkte von f(x) und g(x), sowie von h(x) und i(x)!
c) Zwei Geraden schneiden sich außerhalb des Bildausschnittes. Berechne die Schnittpunkte!
d) Wie viele Schnittpunkte gibt es höchstens bei vier nicht paarweise parallelen Geraden?
5. Gib mögliche Geradengleichungen an!
Zwei aufeinander senkrecht stehende Geraden schneiden sich in S( -2 | -1).
Gib mögliche Geradengleichungen an!
6. Bestimme die Steigung von h!
Die Gerade h steht senkrecht auf der Geraden g. Bestimme die Steigung von h!
a) ![]()
b) ![]()
c) ![]()
7. Ausführliche Aufgabe
Eine Zeitschrift, die zum Preis von 2,20 € zu kaufen ist, hat eine Auflage von 120 000 Exemplaren. Mit Hilfe der Marktforschung stellt der Verlag fest, dass sich die Auflage bei einer Preissenkung um 0,20 € pro Zeitschrift um 5000 Exemplare erhöhen lässt, bei einer Preiserhöhung um 0,20 € verliert man 5000 Käufer.
a) Berechne den Preis bei einer Auflage von 140 000 Exemplaren!
Welcher Stückpreis ergibt sich bei einer Auflage von y Exemplaren?
b) Welche Verkaufszahlen kann der Verlag erwarten, wenn er den Preis derZeitschrift auf 1,50 € senkt?
Dazu findest du die hier die Lösungen.
Die Theorie findest du hier : Lage zweier Geraden zueinander.
Und hier eine Übersicht über weitere Beiträge zu linearen Funktionen, darin auch Links zu weiteren Aufgaben.

