Hier findest du die Lösungen der Aufgaben zu Graphe von Exponentialfunktionen und e-Funktion. Dabei geht es darum e-Funktionen zu verschieben, spiegeln, die Form zu ändern. Außerdem geht es um Grenzwert, Nullstelle, Extremwert, Wendepunkt etc.
Ermittele jeweils die Verschiebungen, Spiegelung und Formänderung der Grundfunktion ex. Zeichne den Funktionsgraphen und die Grundfunktion ex in ein geeignetes Koordinatensystem und berechne den Schnittpunkt mit der y-Achse. Lies Grenzwerte und falls vorhanden Nullstellen, Extremwerte und Wendepunkte am Graphen ab!
1.
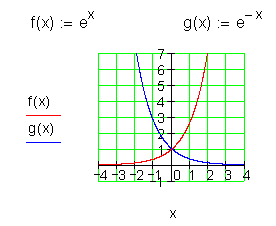
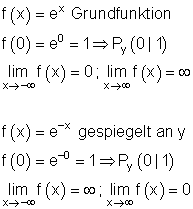
2.
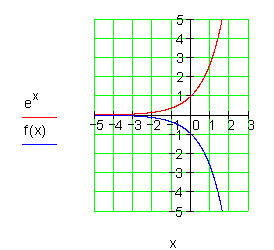
Es gibt also keine Nullstellen.
Außerdem keine Extremwerte.
Ebenso keine Wendepunkte.
3.
Es gibt wieder keine Nullstellen.
Außerdem keine Extremwerte.
Ebenso keine Wendepunkte.
4.
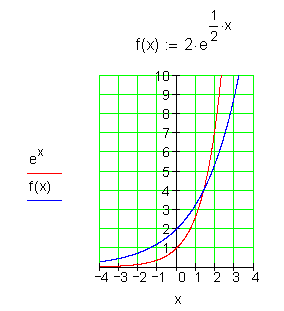
Es gibt also keine Nullstellen.
Ebenso keine Extremwerte.
Außerdem keine Wendepunkte.
5.
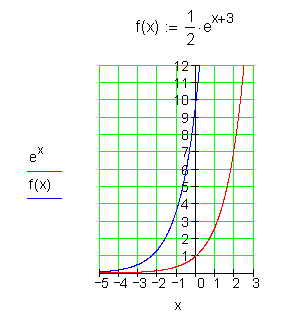
Es gibt also keine Nullstellen.
Außerdem keine Extremwerte.
Ebenso keine Wendepunkte.
6.
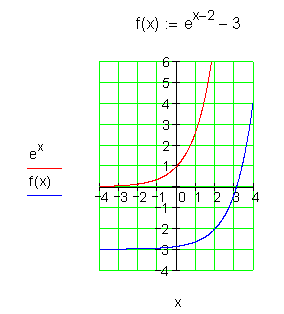
Wird eine e-Funktion gespiegelt, gestreckt, gestaucht oder in x- Richtung verschoben, so schneidet sie die x-Achse nicht, hat also keine Nullstelle. Eine Nullstelle kann es nur dann geben, wenn der Graph in y- Richtung verschoben wird.
7.
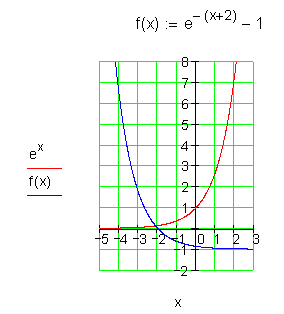
8.
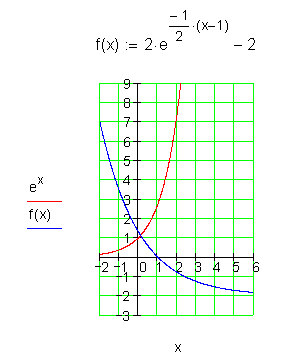
9.
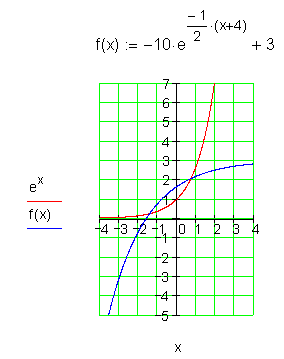
10.
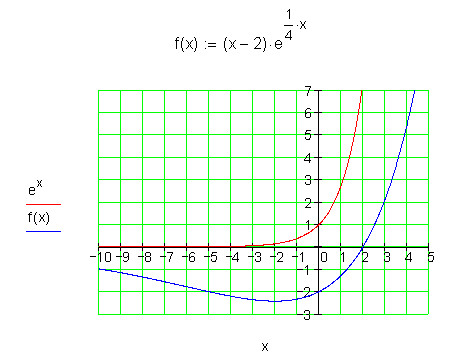
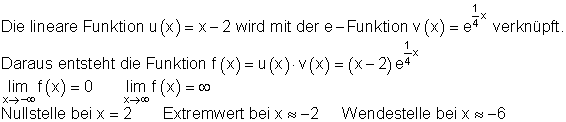
Eine e-Funktion hat keine Extrem- und keine Wendepunkte. Erst wenn eine e-Funktion mit einer anderen Funktion verknüpft wird, können Extrem- und Wendepunkte auftreten.
Hier findest du die Aufgaben Exponentialfunktionen, e-Funktion.
Und hier die Theorie dazu: Exponentialfunktionen und die e-Funktion.
Hier findest du eine Übersicht über alle Beiträge zum Thema Fortgeschrittene Differential- und Integralrechnung, dort auch Links zu weiteren Aufgaben.
