In diesem Beitrag zeige ich zuerst, wie man mit den grafikfähigen Taschenrechnern Casio fx-CG20 und Casio fx-CG 50 das Integral eines gegebenen Intervalls berechnet. Danach erkläre ich anhand von Beispielen die Berechnung des Integralwerts und des Flächeninhalts zwischen zwei oder mehr Nullstellen eines Graphen, in einem beliebigen Intervall und der Fläche zwischen zwei Graphen. Zuletzt zeige ich das Zeichnen der Stammfunktion.
Casio fx-CG20 auf Casio fx-CG50 updaten
Integral eines gegebenen Intervalls
Wir geben die ganzrationale Funktion
![]()
in den Grafikeditor ( [MENU] 5 ) ein und lass sie mit {DRAW} im Grafikfenster anzeigen.
Siehe auch Einstellungen im Betrachtungsfenster
Danach wollen wir das Integral im Intervall [ -3 ; 1 ] berechnen.
So rufen wir die Berechnung auf:
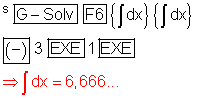
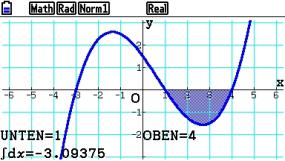
Der Integralwert entspricht dabei der gekennzeichneten Fläche.
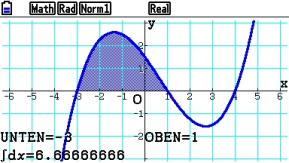
Anschließend wollen wir das Integral im Intervall [ -3 ; 2 ] berechnen.
Zuerst müssen wir die Grafik neu zeichnen. Das geschieht mit S [Sketch] {CLS}.
So rufen wir die Berechnung auf:
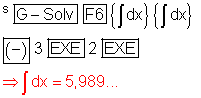
Der Integralwert entspricht jedoch nicht der gekennzeichneten Fläche. Er ist offenbar kleiner.
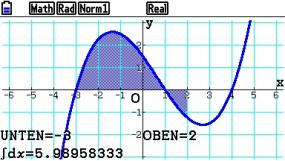
Das Ergebnis der zweiten Rechnung ist kleiner als das der ersten.
Der Grund dafür ist, Flächeninhalte oberhalb der x-Achse werden positiv gezählt, Flächeninhalte unterhalb der x-Achse werden negativ gezählt.
Jetzt wollen wir das Integral im Intervall [ 1 ; 4 ] berechnen:
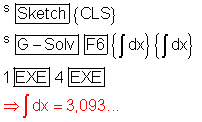
Integralwert und Flächeninhalt zwischen zwei oder mehr Nullstellen eines Graphen
Wir geben die ganzrationale Funktion
![]()
in den Grafikeditor ( [MENU] 5 ) ein und lassen sie mit {DRAW} im Grafikfenster anzeigen.
Siehe auch Einstellungen im Betrachtungsfenster
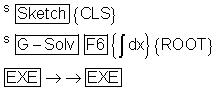
Die Nullstelle ganz links wird automatisch markiert.
Wenn sie für die Berechnung gelten soll, quittieren wir mit [EXE] .
Mit der Cursor-Taste springen wir anschließend zur nächsten oder zur übernächsten Nullstelle.
Der Tastenbefehl [EXE] startet die Berechnung.
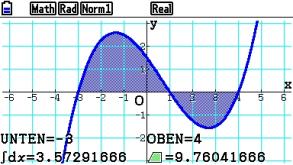
In der Anzeige ist danach der Integralwert (3,572…) und auch die tatsächliche Fläche zwischen dem Graphen und der x-Achse zu sehen.
Der GTR berücksichtigt bei der Flächenberechnung, dass Flächen unterhalb der x-Achse ein negatives Vorzeichen besitzen.
Der Integralwert hingegen setzt sich aus der Addition der positiven und negativen Integralwerte zusammen.
Integralwert und Flächeninhalt in einem beliebigen Intervall
Wir geben diesmal die ganzrationale Funktion
![]()
in den Grafikeditor ( [MENU] 5 ) ein und lassen sie mit {DRAW} im Grafikfenster anzeigen.
Das Integral und der Flächeninhalt sollen im Intervall [ -1 ; 3 ] berechnet werden:
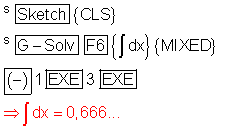
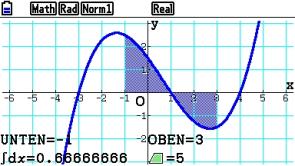
Im Ergebnis wird ein Integralwert von 0,666.. und eine Fläche von 5 Flächeneinheiten (5 FE) angezeigt.
Fläche zwischen zwei Graphen
Diesmal geben wir die ganzrationalen Funktionen
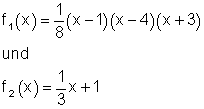
in den Grafikeditor ( [MENU] 5 ) ein und lassen sie mit {DRAW} im Grafikfenster anzeigen.
Die gesamte Fläche zwischen den beiden Graphen soll berechnet werden:
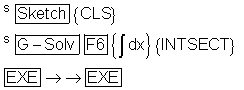
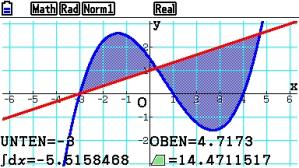
Als Ergebnis wird ein Integralwert von -5,515… und eine Fläche von 14,471 FE angezeigt.
Zeichnen der Stammfunktion
Wir gegen die ganzrationale Funktion
![]()
in den Grafikeditor ( [MENU] 5 ) als Y1 ein und lassen sie mit {DRAW} im Grafikfenster anzeigen.
Danach geben wir bei Y2 den Integrationsbefehl ein.
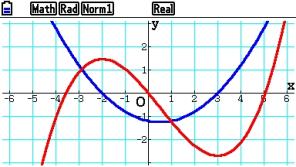
Der Graph von Y1 erscheint dabei sofort im Grafikfenster, der von der Stammfunktion Y2 dauert etwas länger.
Es wird nur ein Repräsentant aus der Menge der Stammfunktionen gezeichnet.
Alle Berechnungen die man im G-Solv-Menü durchführen kann, kann man auch auf die Stammfunktion anwenden. Dazu benötigt der GTR aber einige Zeit.
Er kann z.B. die Fläche zwischen den beiden Graphen berechnen:

Die Rechenprozedur dauert einige Sekunden.
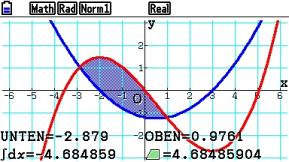 .
.
Weitere Beispiele zu dem Casio fx-CG20 findest du in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.


