In diesem Beitrag zeige ich zuerst, wie man mit den grafikfähigen Taschenrechnern Casio fx-CG20 und Casio fx-CG 50 Extrempunkte bestimmt. Danach erkläre ich an einem Beispiel das Zeichnen der Ableitungen f‘(x) und f‘‘(x). Danach zeige ich, wie man Wendepunkte berechnet. Zuletzt erkläre ich das Berechnen von Tangente und Normale.
Casio fx-CG20 auf Casio fx-CG50 updaten
Casio fx-CG20 Extrempunkte bestimmen
Zur Veranschaulichung wird die ganzrationale Funktion
![]()
ins Grafikmenü des GTR eingegeben.
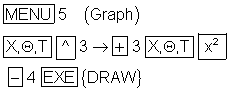 .
.
Um den Grafen optimal anzuzeigen, wird das Grafikfenster mit S [V-Window] auf
x: [ -4 ; 2 ] und y: [ -6 ; 5 ] eingestellt. Siehe auch
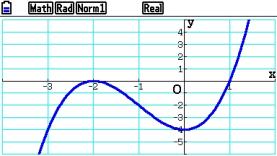
Die Extrempunkte werden mit S [G-Solv] ermittelt.
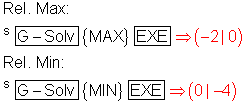
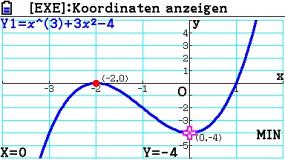
Das relative Maximum liegt bei Pmax ( -2 | 0 ).
Das relative Minimum liegt bei Pmin ( 0 | -4 ).
Falls es mehrere Extrempunkte gibt, lassen sich diese durch Cursorbewegungen (links, rechts) erreichen.
Will man alle Extremwerte, lokal und global, in einem definierten Intervall berechnen, so verwendet man dazu den {FMin} bzw. {FMax}- Befehl.
Da der Funktionsterm in den {FMin} bzw. {FMax}- Befehl eingesetzt werden muss, ist es sinnvoll, den Term zu kopieren und einzusetzen.
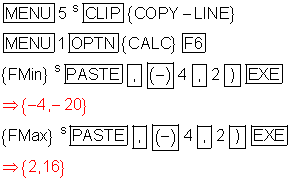

Die Befehle {FMin} und {FMax} benötigen die Eingabe der Intervallgrenzen.
Im Beispiel sind das die Werte x: [ -4 ; 2 ].
Das Ergebnis von {FMin} ist { -4 , -20 } und bedeutet, dass an der Stelle x = -4 mit f(x) = -20 ein absolutes Minimum besteht.
Das Ergebnis von {FMax} ist { 2 , 10 } und bedeutet, dass an der Stelle x = 2 mit f(x) = 16 ein absolutes Maximum besteht.
Zeichnen der Ableitungen f'(x) und f“(x)
Die Gleichungen der Ableitungsfunktionen lassen sich nicht mit dem fx-CG20 berechnen. Die Graphen der Ableitungsfunktionen können jedoch gezeichnet werden.
Die Graphen der ersten und zweiten Ableitung von
![]()
werden gezeichnet. Es wird davon ausgegangen, dass die Funktion sich bereits im Speicher befindet.

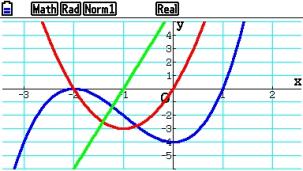
Casio fx-CG20 Wendepunkte berechnen
Für die Funktion
![]()
soll der Wendepunkt berechnet werden.
Es wird davon ausgegangen, dass f(x), f'(x) und f“(x) sich bereits im Speicher befinden.
Die Wendestelle liegt dort, wo die zweite Ableitung Null ist.
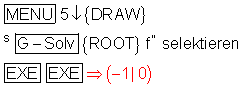
Die Wendestelle ligt bei xw = -1.
Der zugehörige Wendepunkt hat die Koordinaten:
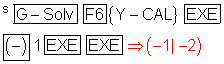
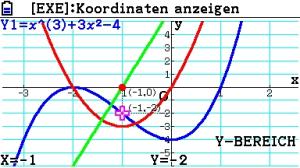
Der Wendepunkt hat die Koordinaten Pw ( -1 | -2 ).
Casio fx-CG20 Tangente und Normale
Damit die Tangentengleichung angezeigt werden kann, muss unter S [SET UP] die Einstellung Derivate auf On gesetzt werden.
![]()
Für die Funktion
![]()
ist die Gleichung der Wendetangente zu ermitteln.
Im Speicher soll sich nur noch die Funktion befinden, für die die Tangente zu ermitteln ist. Ableitungsfunktionen, falls vorhanden, sollten gelöscht werden.
Zunächst wird ein Bereich um den Wendepunkt herausgezoomt.
[MENU] 5 {DRAW} S [ZOOM] {BOX} Anfangspunkt wählen [EXE]
Box auswählen [EXE]. Siehe auch
Gleiche Achsenabstände einstellen.
S [V-Window] {SQUARE} {Y-BASE} [EXE] {DRAW}
Die Koordinaten des Wendepunktes sind bekannt:
Pw ( -1 | 2 )

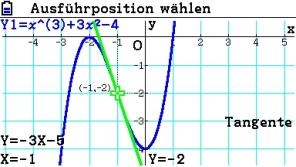
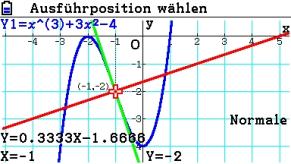
Die Normale durch den Wendepunkt findet man auf ähnliche Weise.
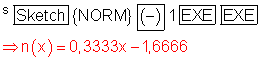
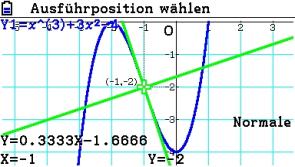
Um Tangente und Normale besser vom Graphen und voneinander unterscheiden zu können, lassen diese sich formatieren.

Dazu findest du weitere Beispiele in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.

