Hier findest du die Aufgaben für lineare und quadratische Funktionen Teil I. Die Lösungen dazu sind weiter unten.
1. Berechne die Achsenschnittpunkte der folgenden Geraden:
![]()
2. Gerade mit vorgegebener Steigung durch einen Punkt.
Die Steigung einer Geraden sei m = 2. Sie soll durch den Punkt P ( -3 | 5 ) verlaufen.
Berechnedie Funktionsgleichung.
3. Gerade durch 2 Punkte.
Gegeben sind die Punkte P1 (-3 | 5 )und P2 (2 | -1 ).
Berechne die Funktionsgleichung.
4. Schnittpunkt zweier Geraden.
Berechne den Schnittpunkt zweier Geraden mit den Funktionsgleichungen:
![]()
5. Die zu einer Geraden senkrecht verlaufende Gerade.
Berechne die zu einer Geraden senkrecht verlaufende Gerade durch den Punkt P.
![]()
6. Achsenschnittpunkte einer Parabel.
Berechne die Achsenschnittpunkte folgender Parabel und zeichne den Graphen.
![]()
Hinweis: Die x-Koordinate des Scheitelpunktes liegt symmetrisch zu den Nullstellen.
7. Scheitelpunktform, Scheitelpunktkoordinaten.
Berechne die Scheitelform der Funktion f(x) und ermittele die Scheitelkoordinaten.
![]()
Dazu kannst du dir das 📽️Video Quadratische Ergänzung Scheitelpunkt bestimmen ansehen.
8. Schnittpunkt von Parabel und Gerade.
Eine Parabel wird von einer Geraden geschnitten. Bestimme die Schnittpunkte.
![]()
Dazu kannst du dir das 📽️Video Schnittpunkt Parabel und Gerade ansehen.
9. Schnittpunkt zweier Parabeln.
Berechne die Schnittpunkte der beiden Parabeln und den Abstand der Scheitelpunkte.
![]()
10. Parabel durch drei Punkte.
Berechne die Funktionsgleichung der Parabel, die durch die Punkte
P1( -1 | -1 ) und P2( 2 | -2 ) sowie P3( 3 | 1 ) verläuft.
Dazu kannst du dir das 📽️Video Funktionsgleichung Parabel durch drei Punkte ansehen.
11. Der Gauß- Algorithmus.
Löse das Gleichungssystem mit dem Gauss- Algorithmus:
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
a)
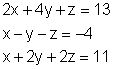
b)
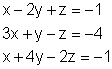
Lösungen:
1. Achsenschnittpunkte einer Geraden.
Berechne die Achsenschnittpunkte der folgenden Geraden:
![]()


2. Gerade mit vorgegebener Steigung durch einen Punkt.
Die Steigung einer Geraden sei m = 2. Sie soll durch den Punkt P ( -3 | 5 ) verlaufen. Berechne die Funktionsgleichung der Geraden.
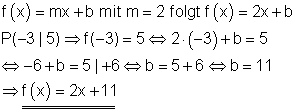
Vorgehensweise:
1. Der Wert der Steigung und die Koordinaten des Punktes P werden in die Funktionsgleichung eingesetzt.
2. Die so entstandene Gleichung wird nach b aufgelöst.
3. Gerade durch 2 Punkte.
Gegeben sind die Punkte P1 (-3 | 5 )und P2 (2 | -1 ). Berechne die Funktionsgleichung der Geraden, die durch diese beiden Punkte verläuft.
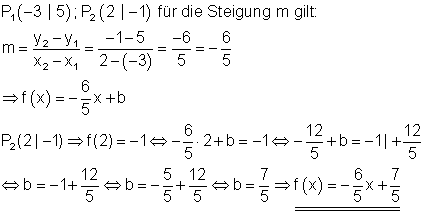
Vorgehensweise:
1. Die Steigung m wird mit der Steigungsformel berechnet.
2. Die Koordinaten eines der beiden Punkte (hier P2) werden in die Funktionsgleichung eingesetzt.
3. Die so entstandene Gleichung wird nach b aufgelöst.
4. Schnittpunkt zweier Geraden.
Berechne den Schnittpunkt zweier Geraden mit den Funktionsgleichungen:
![]()
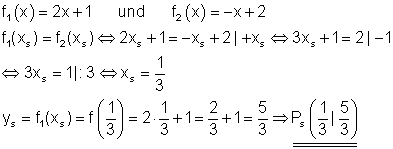
Vorgehensweise:
Für den Schnittpunkt beider Geraden gilt:
f1(xs) = f2(xs).
Das Gleichsetzen beider Funktionsgleichungen liefert die x-Koordinate des Schnittpunktes.
Den y-Wert erhält man durch Einsetzen des Wertes in eine der beiden Funktionsgleichungen.
5. Die zu einer Geraden senkrecht verlaufende Gerade.
Berechne die zu einer Geraden senkrecht verlaufende Gerade durch den Punkt P.
![]()
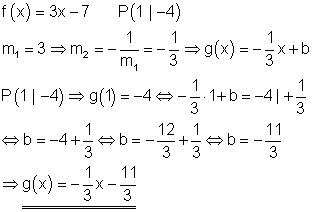
Vorgehensweise:
Zuerst wird die Steigung m2 der senkrechten Geraden aus der Steigung der bekannten Geraden bestimmt.
![]()
Die x-Koordinate von P wird in die Gleichung eingesetzt. Daraus lässt sich dann b errechnen.
6. Achsenschnittpunkte einer Parabel.
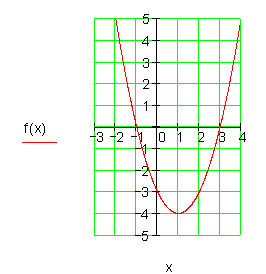
Berechne die Achsenschnittpunkte folgender Parabel und zeichne den Graphen.
![]()
Hinweis: Die x-Koordinate des Scheitelpunktes liegt symmetrisch zu den Nullstellen.
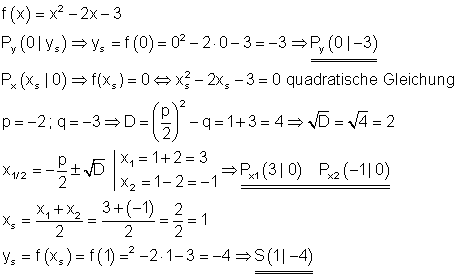
Vorgehensweise:
Die x-Koordinate des Scheitelpunktes liegt symmetrisch zu den Nullstellen.
Der Schnittpunkt mit der y-Achse hat die x-Koordinate 0, also f(0) = ys.
Schnittpunkte mit der x-Achse haben die y-Koordinate 0, also f(xs) = 0.
Das führt auf eine quadratische Gleichung, deren Lösung die x-Koordinaten derAchsenschnittpunkte sind.
Der Graph einer quadratischen Funktion ist eine Parabel.
Jede Parabel ist symmetrisch zu der Achse, die durch den Scheitelpunkt führt.
Falls es Schnittpunkte mit der x-Achse gibt, liegen auch diese symmetrisch zu der Scheitelachse.
Die x-Koordinate des Scheitelpunktesliegt genau in der Mitte zwischen den Nullstellen.
7. Scheitelpunktform, Scheitelpunktkoordinaten.
Berechne die Scheitelform der Funktion f(x) und ermittele die Scheitelkoordinaten.
![]()
Der Koeffizient von x2 wird ausgeklammert.
In der eckigen Klammer wird eine quadratische Ergänzung durchgeführt.
Nach Multiplikation mit dem Koeffizienten erhält man die Scheitelpunktform, aus der sich die Scheitelkoordinaten ablesen lassen.
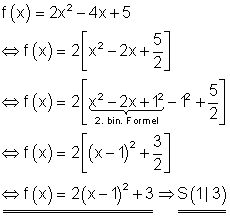
8. Schnittpunkt von Parabel und Gerade.
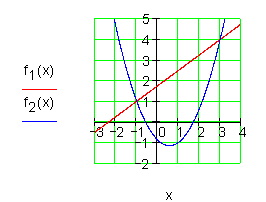
Eine Parabel wird von einer Geraden geschnitten. Bestimme die Schnittpunkte.
![]()
Für den Schnittpunkt der Geraden mit der Parabel gilt:
![]()
Das Gleichsetzen beider Funktionsgleichungen liefert eine quadratische Gleichung. Deren Lösung liefert die x- Koordinaten für den Schnittpunkt.
Die dazugehörigen y-Koordinaten erhält man durch Einsetzen der Werte in f1 oder f2.
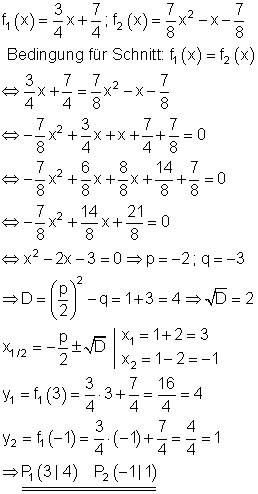
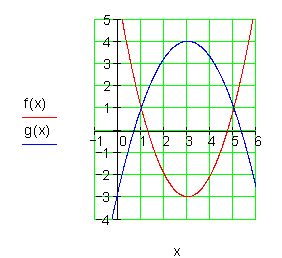
9. Schnittpunkt zweier Parabeln.
Berechne die Schnittpunkte der beiden Parabeln und den Abstand der Scheitelpunkte.
![]()
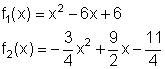
Für den Schnittpunkt beider Parabeln gilt:
![]()
Das Gleichsetzen beider Funktionsgleichungen liefert eine quadratische Gleichung. Deren Lösung liefert die x- Koordinaten für den Schnittpunkt.
Die dazugehörigen y-Koordinaten erhält man durch Einsetzen der Werte in f1 oder f2.
Da beide y-Koordinaten auf gleicher Höhe liegen und aus der Symmetrie der Parabel findet man die x- Koordinate der Scheitelpunkte. Damit gelangt man an die Scheitelkoordinaten und kann den Abstand bestimmen.

10. Parabel durch drei Punkte.
Berechne die Funktionsgleichung der Parabel, die durch die Punkte
P1( -1 | -1 ) und P2( 2 | -2 ) sowie P3( 3 | 1 ) verläuft.
Durch Einsetzen der Koordinaten der drei Punkte in die allgemeine Funktionsgleichung entsteht ein Gleichungssystem mit drei Variablen.
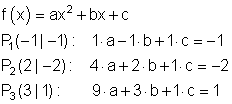
Dieses ist mit den Gauß-Algorithmus lösbar und liefert die Koeffizienten a, b und c.
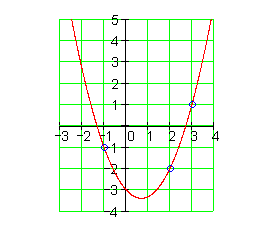
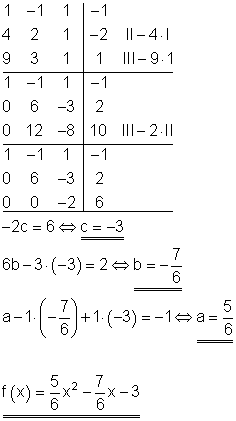
11. Der Gauß-Algorithmus.
Löse das Gleichungssystem mit dem Gauß-Algorithmus:
a)
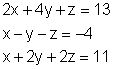
b)
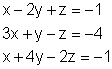
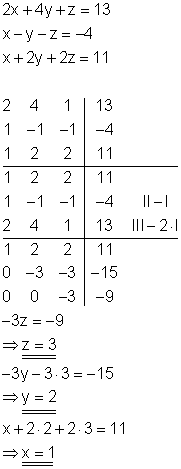
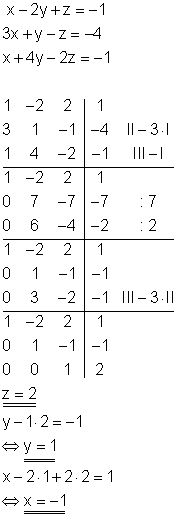
Dazu findest du hier eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu weiteren Aufgaben.

