Hier findest du die Lösungen der Aufgabe zur Differentialrechnung IX, dabei geht es unter anderem darum, Kurvenpunkte zu berechnen.
1. a)
Dazu kannst du die das 📽️ Video Extrempunkte in der Differentialrechnug ansehen.
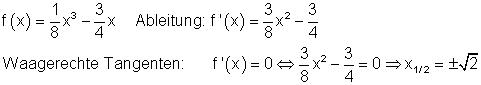
Die Ableitung f'(x) hat bei x1/2 einfache Nullstellen und wechselt das Vorzeichen.
Also hat f(x) zwei Extrempunkte.
1. b)
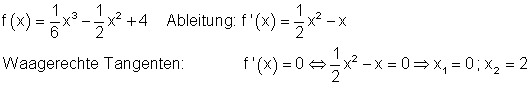
Die Ableitung f'(x) hat bei x1/2 einfache Nullstellen und wechselt das Vorzeichen.
Also hat f(x) zwei Extrempunkte.
1. c)
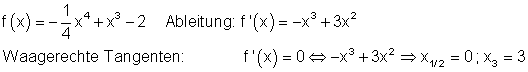
Die Ableitung f'(x) hat an der Stelle x1/2 = 0 eine doppelte Nullstelle, das bedeutet, es findet kein Vorzeichenwechsel statt. Also hat f(x) an dieser Stelle keinen Extrempunkt. x3 = 3 ist einfache Nullstelle von f'(x), dort findet ein Vorzeichenwechsel statt.
Also hat f(x) an dieser Stelle einen Extrempunkt.
2.
Dazu kannst du die das 📽️ Video Extrempunkte hinreichende Bedingung ansehen.

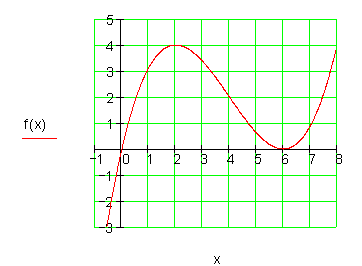
3.
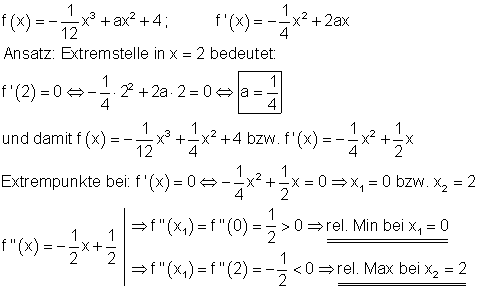
4.

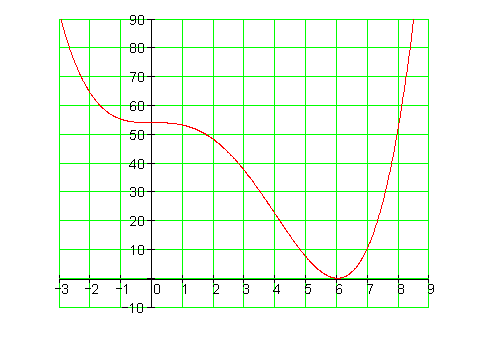
5.
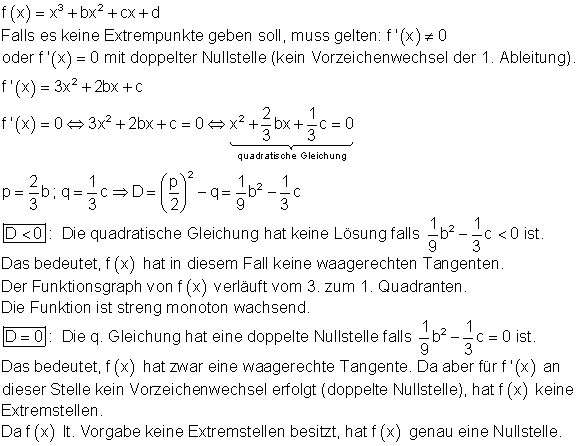
6.
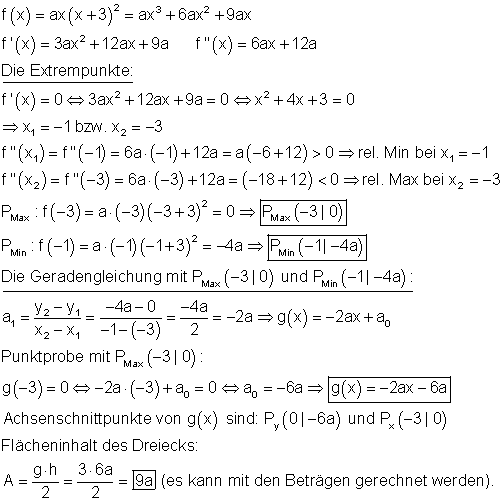

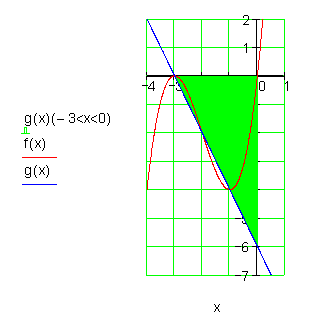
7.
a)

7. b)
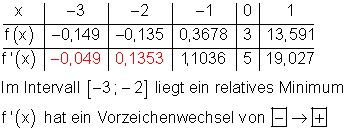
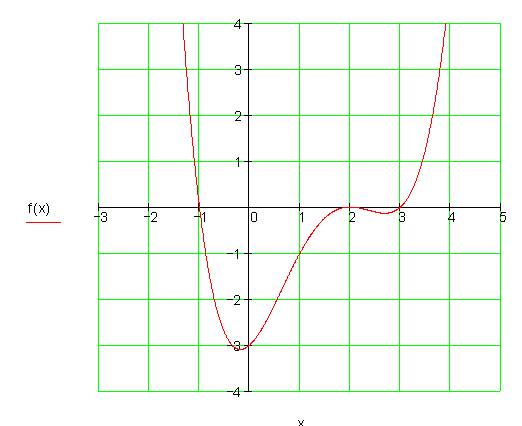
8. a)
Dazu kannst du dir das 📽️Video Wendepunkte ansehen.


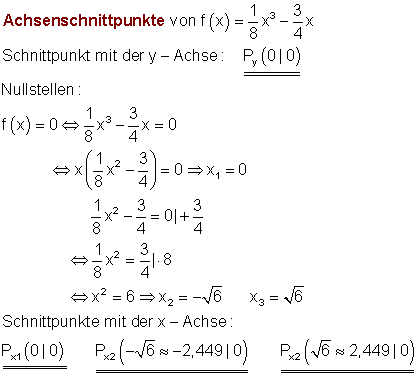
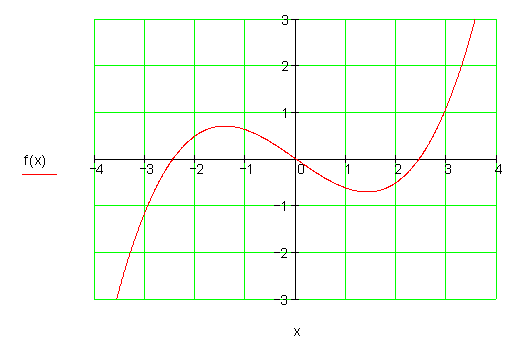
8. b)



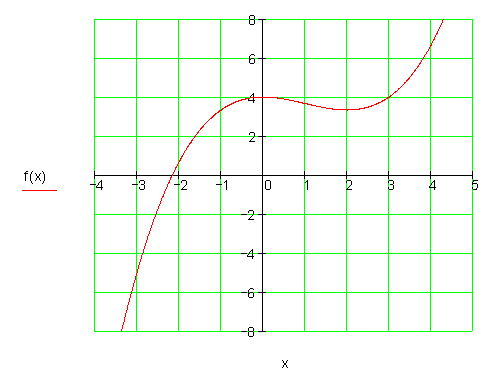
8. c)
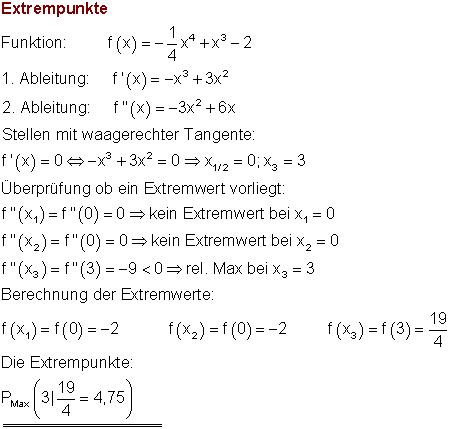


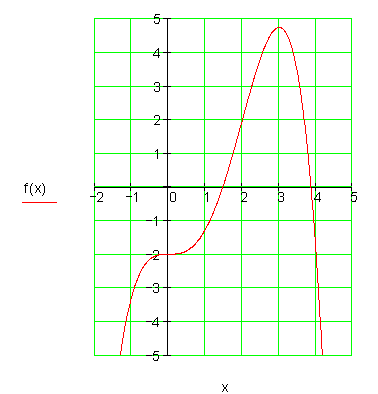
8. d)


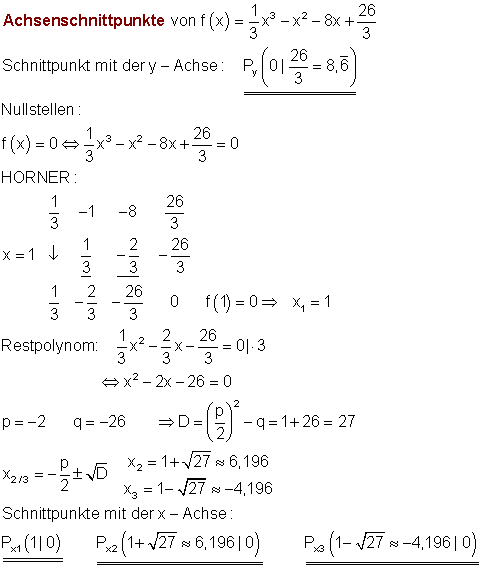
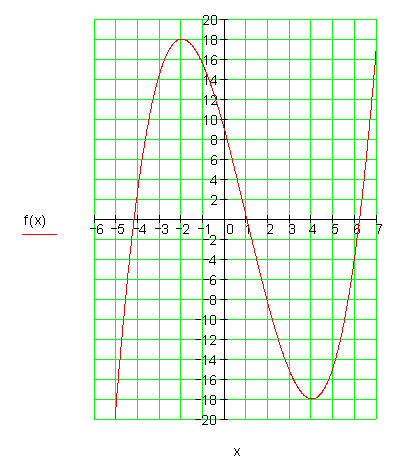
8. e)

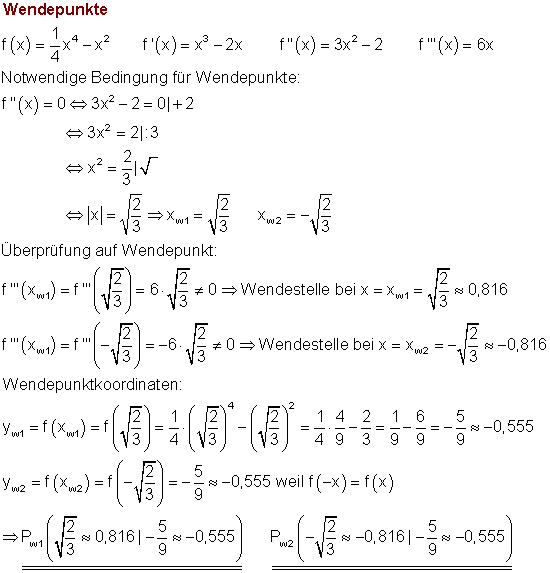

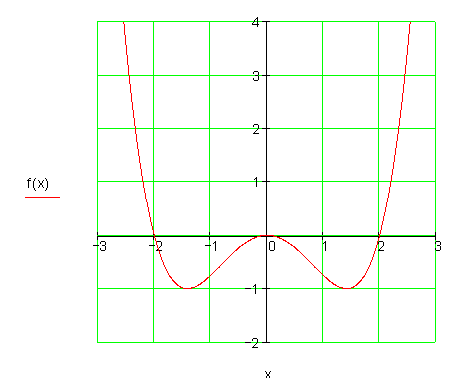
8. f)
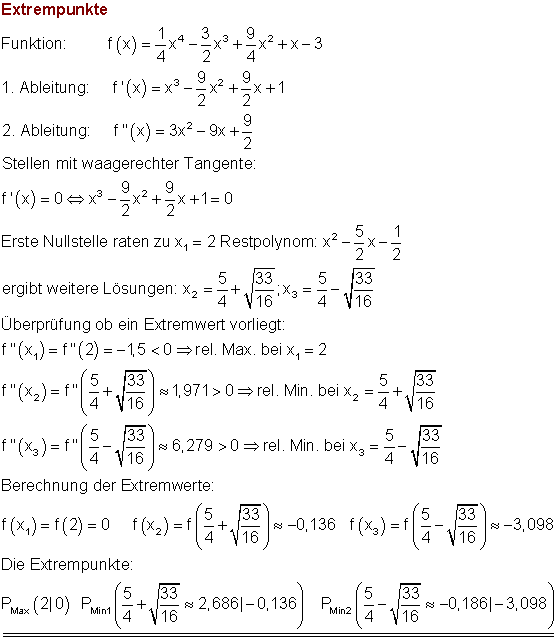
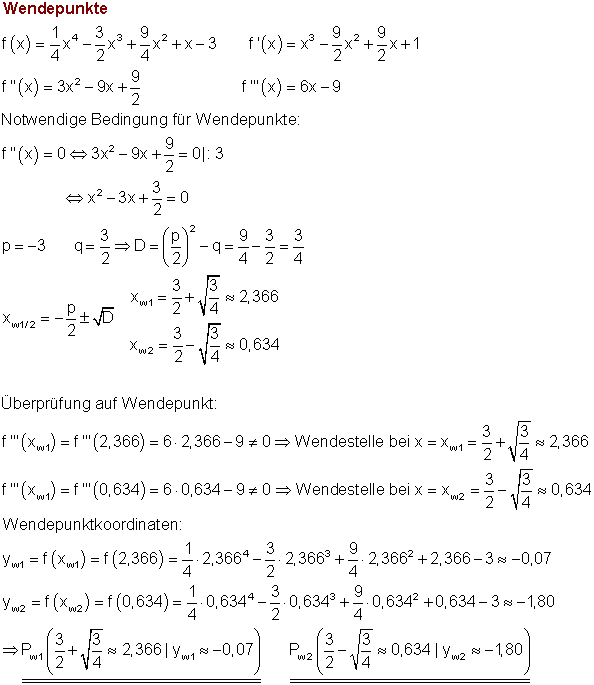
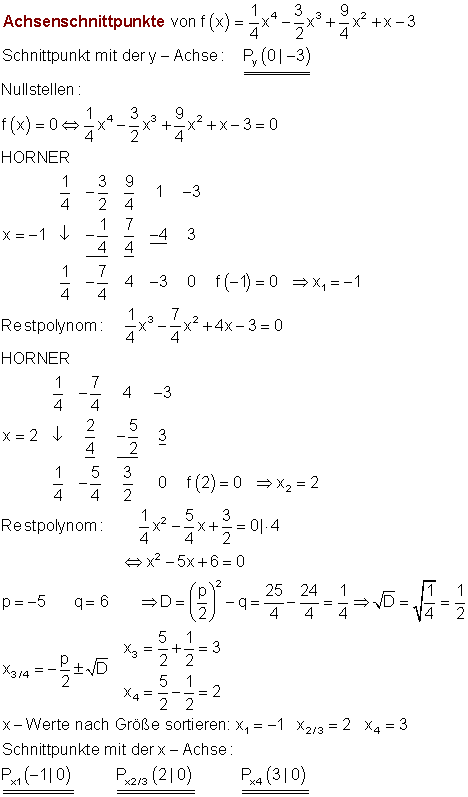
8. g)
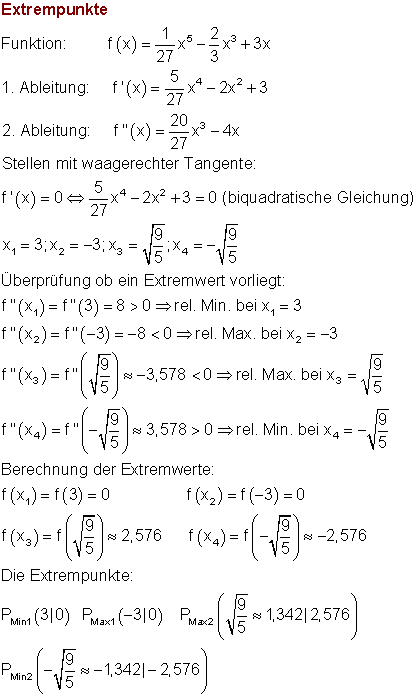
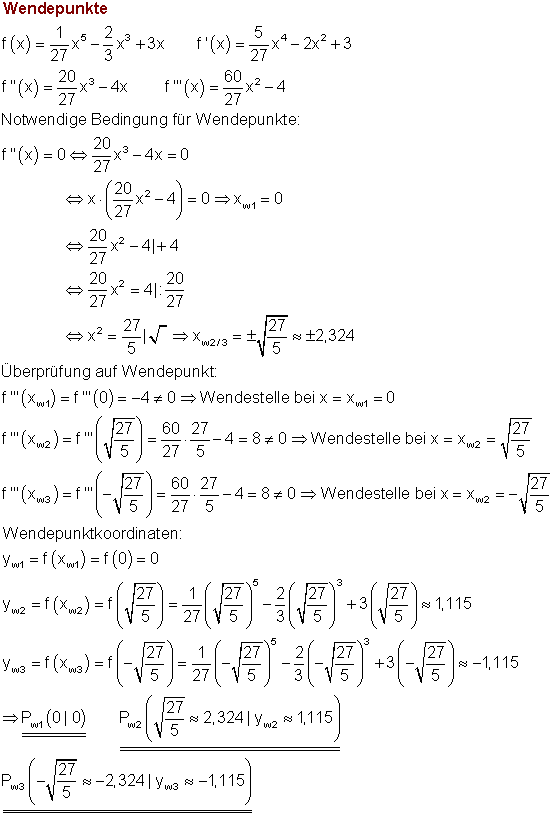
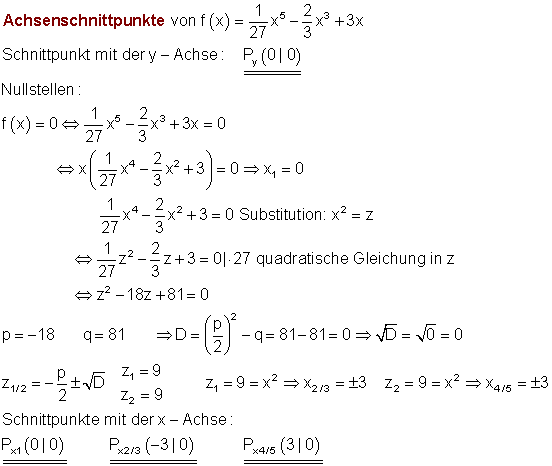
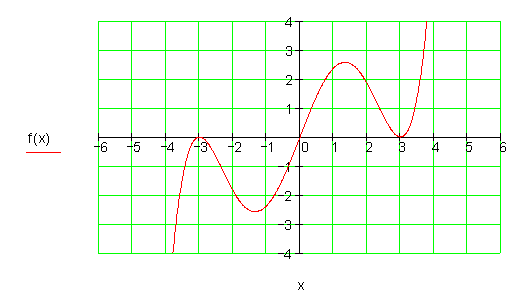
Hier findest du die Aufgaben hierzu
und hier weitere Trainingsaufgaben
und hier die Theorie: Extrempunkte berechnen
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.

