Hier findest du die Lösungen der Aufgaben zur Integralrechnung II mit komplettem Lösungsweg, darin geht es um die Berechnung einfacher Flächen.
1. a) Ausführliche Lösung:
Die Fläche liegt unterhalb der x- Achse und ist negativ. Zu überprüfen ist, ob die Integrationsgrenzen mit den Nullstellen übereinstimmen.
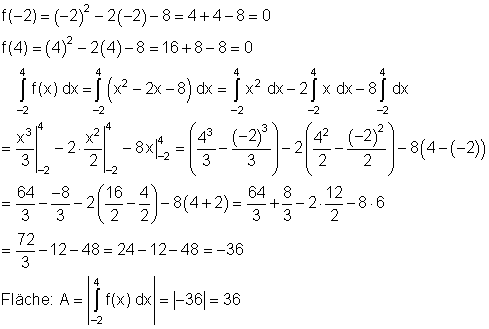
Der Flächeninhalt beträgt 36 FE.
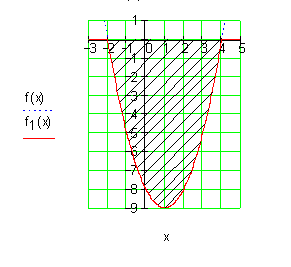
1. b) Ausführliche Lösung:
Die Fläche liegt unterhalb der x- Achse und ist negativ. Zu überprüfen ist, ob die obere Integrationsgrenze mit der Nullstelle übereinstimmt.
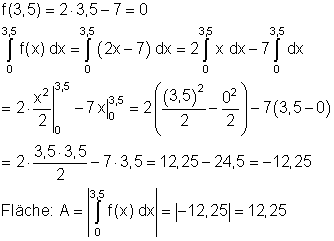
Der Flächeninhalt beträgt 12,25 FE. Da es sich bei der abgebildeten Fläche um ein Dreieck handelt, hätte man das Ergebnis auch einfacher bekommen können:
![]()
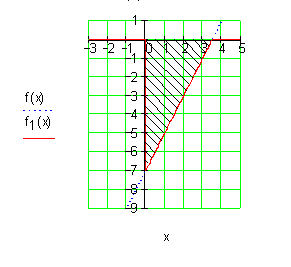
1. c) Ausführliche Lösung:
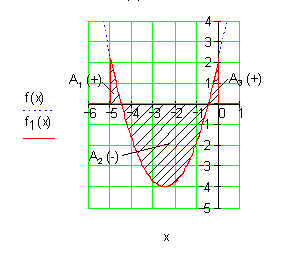
Die Flächen A1 und A3 liegen oberhalb der x- Achse und sind positiv. Die Fläche A2 liegt unterhalb der x- Achse und ist negativ. Um die Integrationsgrenzen für alle Teilintegrale zu bekommen, müssen zuerst die Nullstellen von f(x) bestimmt werden.
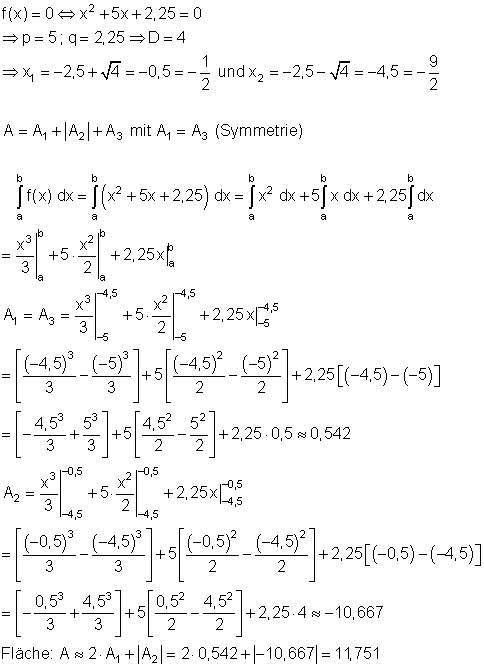
Der Flächeninhalt beträgt etwa 11,751 FE.
1. d) Ausführliche Lösung:
Die Fläche A1 liegt unterhalb der x-Achse, sie zählt negativ.
Die Fläche A2 liegt oberhalb der x-Achse, sie zählt positiv.
Um die Integrationsgrenzen für die beiden Teilintegrale zu bekommen, muss zuerst die Nullstelle von f(x) bestimmt werden.
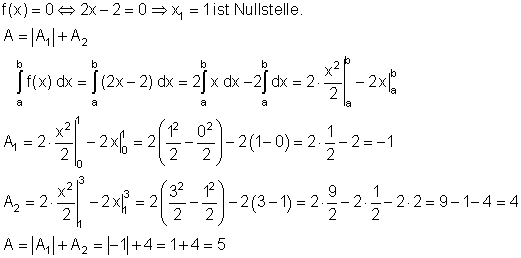
Der Flächeninhalt beträgt 5 FE.
Zum gleichen Ergebnis gelangt man auch über die Berechnung beider Dreiecke.
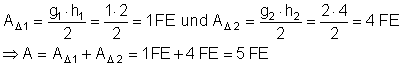
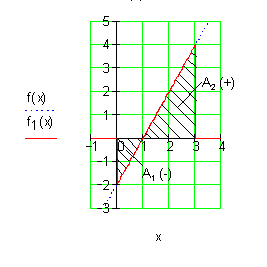
2. a) Ausführliche Lösung:
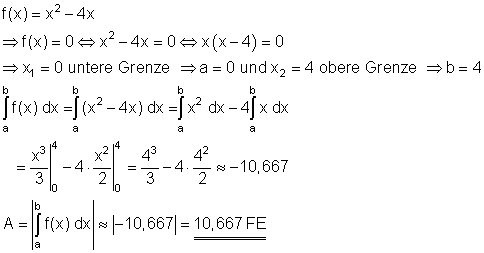
Der Flächeninhalt beträgt etwa 10,667 FE.
2. b) Ausführliche Lösung:
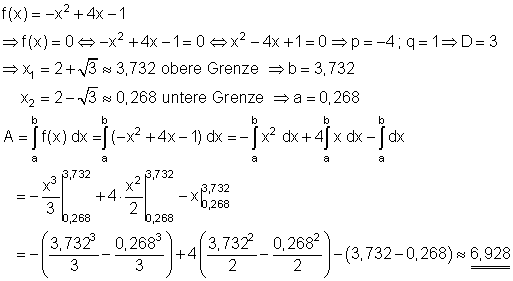
Die gekennzeichnete Fläche hat einen Flächeninhalt von etwa 6,928 FE.
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie hier: Fächenberechnung.
Hier eine Übersicht über alle Beiträge zur Integralrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.