Hier findest du die Lösungen der Aufgaben zu Logarithmusfunktionen.
Zeichne jeweils den Graphen und lese die Verschiebungen und Formänderung der Grundfunktion ln (x), sowie Achsenschnittpunkte, Grenzwerte und Extremwerte ab.
1.
f(x) = ln für (0; 8]
Ausführliche Lösung :
f(x) = ln(x) Grundfunktion
Nullstelle bei x = 1, denn f(1) = ln(1) = 0
\lim \limits_{x \to \infty} f(x) = \infty \\
\lim \limits_{x \to 0^+} f(x) = -\infty
nur für positive x-Werte definiert \mathbb{R}_+^* . 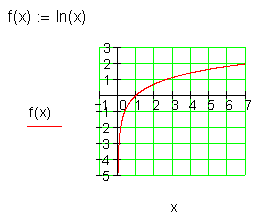
Besonderheiten der Logarithmusfunktion. Die Logarithmusfunktion ist nur für positive x-Argumente definiert. Im Intervall ( 0 ; 1 ) ist der Logarithmus einer Zahl negativ. Für die Zahl 1 ist er Null. Im Intervall (1 ; unendlich) ist er positiv. Extremwerte und Wendestellen existieren nicht.
2.
f(x) = ln (-x) für [-8 ; 0)
Ausführliche Lösung:

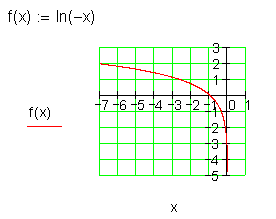
3.
f(x) = ln (x2) für [-4 ; 0) und (o ; 4]
Ausführliche Lösung:
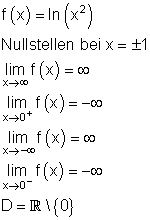
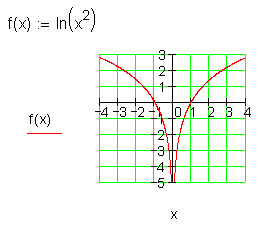
4.
f(x) 0 ln (x – 1) + 2 für (1 ; 9]
Ausführliche Lösung:

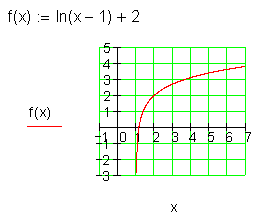
5.
f(x) = \frac{1}{2} ln (x) +1 \quad für \quad (0 ; 8]
Ausführliche Lösung:

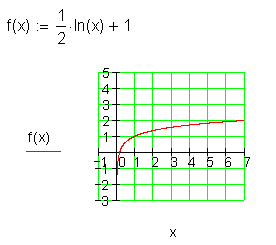
6.
f(x) = x \cdot ln(x) \quad für \quad (0 ; 8]
Ausführliche Lösung:
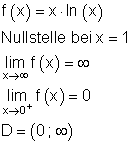
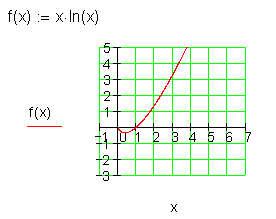
Bei Verknüpfung einer Logarithmusfunktion mit einer anderen Funktion kann es auch Extrem- und Wendepunkte geben.
7.
f(x) = -x \cdot ln(-x) \quad für \quad [-8 ; 0]
Ausführliche Lösung:
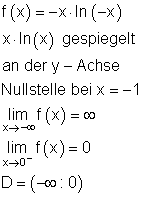
Es existiert ein relatives Minimum.
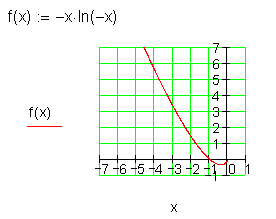
8.
f(x) = ln (x + 4) -3 \quad für \quad (-4 ; 4]
Ausführliche Lösung:

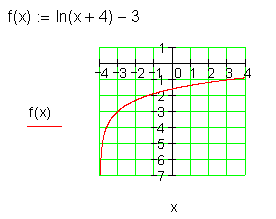
9.
f(x) = e^{\frac{1}{4} x} \cdot \ln({\frac{x}{4}}) \quad für \quad (0 ; 8 ]
Ausführliche Lösung:
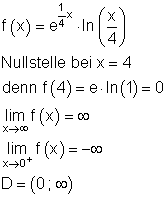
Wendestelle und Nullstelle existieren.
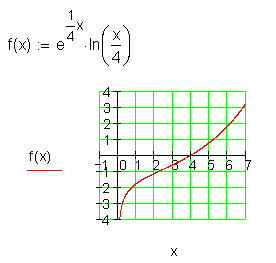
10.
f(x) = 2 \cdot e^{\frac{1}{4} x^2} \cdot \ln({\frac{x}{4}}) \quad für \quad (0 ; 8 ]
Ausführliche Lösung
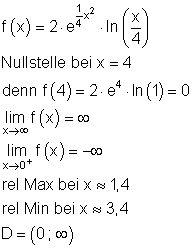
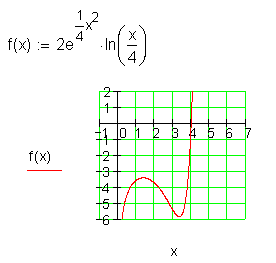
Hier findest du die Aufgaben hierzu.
Und hier findest du eine Übersicht über alle Beiträge zum Thema Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

