Zuerst wiederhole ich hier die wichtigsten Eigenschaften einer Funktion. Danach biete ich einen Überblick über die wichtigsten Funktionsklassen mit vielen Beispielen. Darunter sind Umkehrfunktionen, transzendente Funktionen etc. Außerdem gibt es Aufgaben zu Graphen von e-Funktionen und Logarithmusfunktionen.
- Die wesentliche Eigenschaft einer Funktion:
- Rationale Funktionsklasse
- Gebrochenrationale Funktionsklasse n-ten Grades
- Transzendente Funktionsklasse
- Exponentialfunktionsklasse
- Die e-Funktion als besondere Exponentialfunktion
- Trainingsaufgaben: Graphen von e-Funktionen
- Logarithmusfunktionsklasse
- Trainingsaufgaben: Graphen von Logarithmusfunktionen
- Wurzelfunktionsklasse
- Trigonometrische Funktionsklasse
- Die Betragsfunktion
- Zusammengesetzte Funktionen
- Umkehrfunktionsklasse
- Die gaußsche Glockenkurve
Bisher haben wir nur ganzrationale Funktionen kennen gelernt. In der modernen Mathematik spielen jedoch noch weitere Funktionen und Funktionsklassen eine große Rolle. Weil ich auf dieser Webseite nicht alle Funktionsklassen behandele, gebe ich in diesem Beitrag einen Überblick über die wichtigsten Funktionsklassen mit vielen Beispielen. Außerdem stelle ich Trainingsaufgaben zu e-Funktionen und Logarithmusfunktionen zur Verfügung.
Die wesentliche Eigenschaft einer Funktion:
Jedem Wert der unabhängigen Variablen (x) wird genau ein Funktionswert f(x) zugeordnet.
Die Definitionsmenge (D) einer Funktion ist die Menge aller unabhängigen Variablen, für die die Funktionsgleichung definiert ist.
Die Wertemenge (W) ist die Menge aller Funktionswerte, sie hängt auch von der Definitionsmenge ab.
Dies habe ich in dem Beitrag Funktionen in der Mathematik ausführlich erklärt.
Dazu gibt es auch einen Artikel auf Wikipedia.
Rationale Funktionsklasse
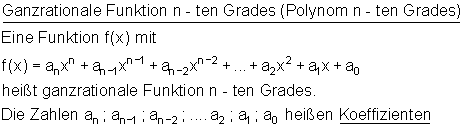
Ganzrationale Funktionen entstehen durch Zusammensetzen von Potenzfunktionen.
Der Verlauf des Graphen einer ganzrationalen Funktion wird dabei durch den Summanden mit der höchsten Potenz bestimmt. Die Definitionsmenge ist normalerweise die Menge der reellen Zahlen. Eine ganzrationale Funktion n-ten Grades hat höchstens n Nullstellen.
Hier der Verlauf des Graphen ganzrationaler Funktionen:
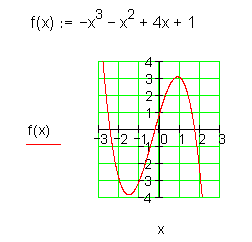
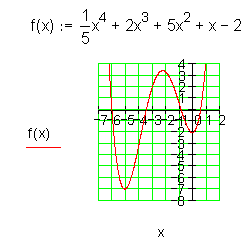
Gebrochenrationale Funktionen n-ten Grades:

Die Definitionsmenge gebrochenrationaler Funktionen ist eingeschränkt. Überall dort, wo der Nenner Null wird, ist die Funktion nicht definiert.
Hier der Verlauf des Graphen gebrochenrationaler Funktionen:
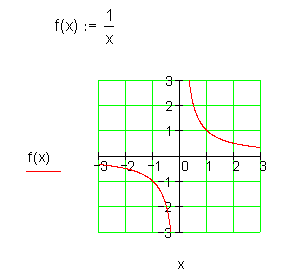
Hyperbel punktsymmetrisch
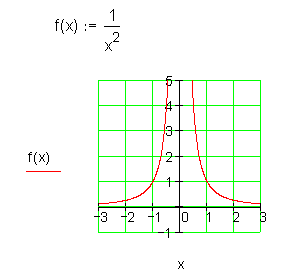
Hyperbel achsensymmetrisch
Beide Funktionen sind an der Stelle x = 0 nicht definiert.
Transzendente Funktionsklasse
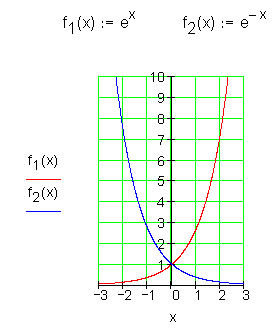
Exponentialfunktionsklasse
![]()
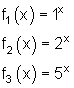
Alle Graphen nebenstehender Exponentialfunktionen verlaufen durch den Punkt ( 0 | 1 ).
Je größer die Basis a ist, desto steiler ist der Kurvenverlauf.
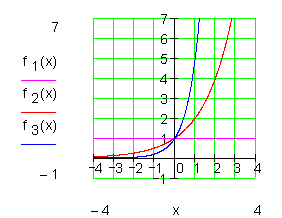
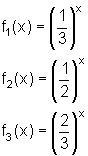
Alle Graphen nebenstehender Exponentialfunktionen verlaufen durch den Punkt ( 0 | 1 ).
Je kleiner die Basis a ist, desto steiler ist der Kurvenverlauf
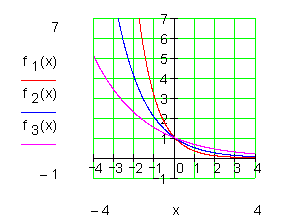
Die e-Funktion als besondere Exponentialfunktion:
Die Graphen verlaufen von II nach I
Ist der Exponent positiv, so ist der Graph monoton steigend.
Ist der Exponent negativ, so ist der Graph monoton fallend.
Es gibt keine Nullstellen.
Für große x – Beträge nähert sich der Graph immer mehr der x – Achse.
Alle Graphen verlaufen durch den Punkt
P ( 0 | 1 ).
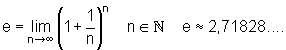
Trainingsaufgaben: Graphen von e-Funktionen
Berechne Verschiebungen, Spiegelung und Formänderung der Grundfunktion ex.
Zeichne jeden Funktionsgraphen und die Grundfunktion ex in ein geeignetes Koordinatensystem und berechne den Schnittpunkt mit der y-Achse.
Lies an dem Graphen ab:
Grenzwerte und falls vorhanden Nullstellen, Extremwerte und Wendepunkte.
Bemerkung: Berücksichtige nur die Funktionswerte, die im Intervall [ -10 ; 10 ] liegen.
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
Hier findest du die Lösungen.
Logarithmusfunktionsklasse
Logarithmusfunktionen sind nur für positive x-Werte definiert.
Alle Graphen verlaufen durch den Punkt P ( 1 | 0 ).
Logarithmusfunktionen sind die Umkehrfunktionen von Exponentialfunktionen.
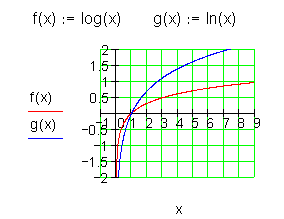
Trainingsaufgaben: Graphen von Logarithmusfunktionen.
Zeichne die Graphen folgender Logarithmusfunktionen und lies daraus ab:
Verschiebungen und Formänderung der Grundfunktion ln (x) , Achsenschnittpunkte, Grenzwerte und Extremwerte.
(Nur die Funktionswerte sind zu berechnen, die im Bereich [ -10 ; 10 ] liegen)
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.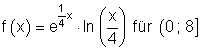
10.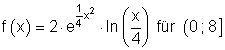
Hier findest du die Lösungen.
Wurzelfunktionsklasse
Außerdem sind sie die Umkehrfunktionen von Potenzfunktionen.
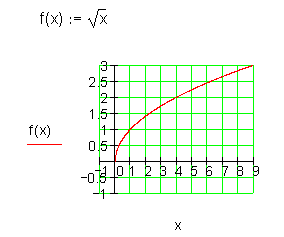
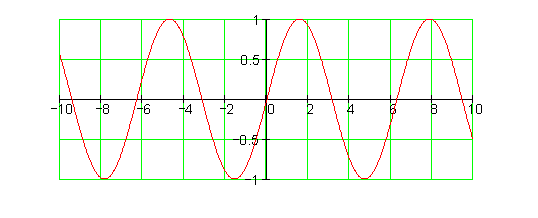
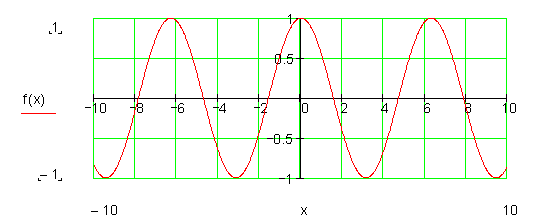
Trigonometrische Funktionsklasse


Die Betragsfunktionsklasse

Für alle x-Werte ist sie positiv. An der Stelle x = 0 ist sie unstetig.
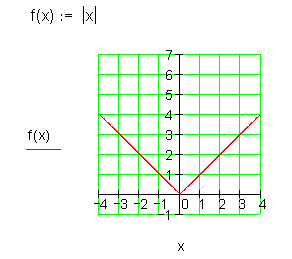
Zusammengesetzte Funktionen
Aus allen bisher bekannten Funktionen lassen sich weitere Funktionen zusammensetzen. Dazu ein paar Beispiele:
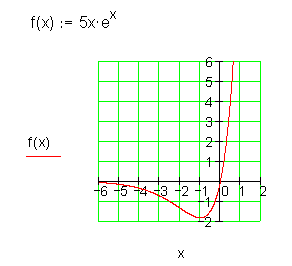
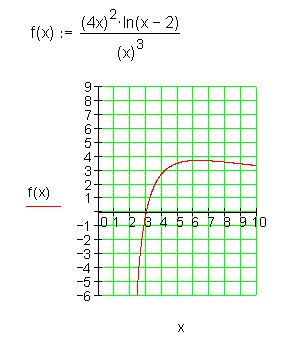
Umkehrfunktionsklasse

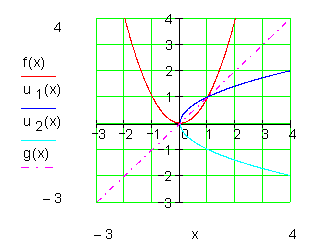

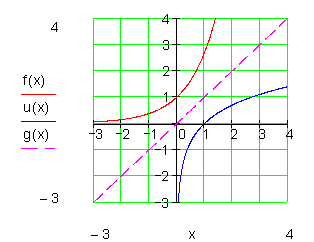
In beiden Fällen ist der Graph der Umkehrfunktion eine Spiegelung der Graphen der Ursprungsfunktion an der Geraden g(x) = x.
Das gilt für alle Funktionen und deren Umkehrfunktionen.
Die gaußsche Glockenkurve
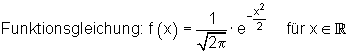
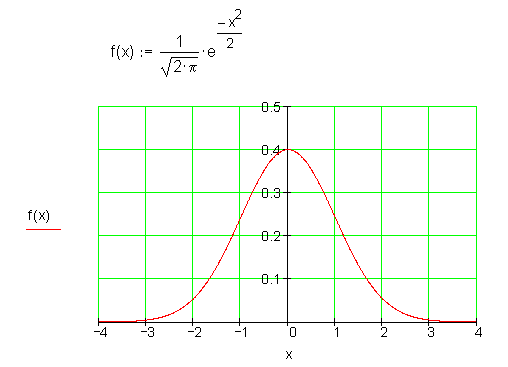
Eigenschaften:
Die Funktion ist achsensymmetrisch.
Die Funktion erreicht in der Mitte bei x = 0 den höchsten Wert.
Nach rechts und links fallen die Werte sehr schnell ab.
Nennenswerte Funktionswerte liegen nur im Bereich von -3 bis +3
Die Ergebnisse von Klassenarbeiten oder psychologischer Tests verteilen sich oft in dieser Form.
Betrachtet man die Fläche unter der Kurve, so beträgt der Anteil, der im Bereich von -1 bis + 1 liegt etwa 68%, das ist etwa 2/3 der Gesamtfläche.
Bei IQ-Messungen haben die meisten Testpersonen einen IQ zwischen 70 und 130.
Nur wenige liegen darunter oder darüber. So dass der Mittelwert bei etwa 100 liegt.
Um diesen Sachzusammenhang mit der gaußschen Glockenkurve zu veranschaulichen, muss die Mitte zu dem Wert 100 verschoben werden. Auch die Streuung um den Mittelwert wird berücksichtigt.
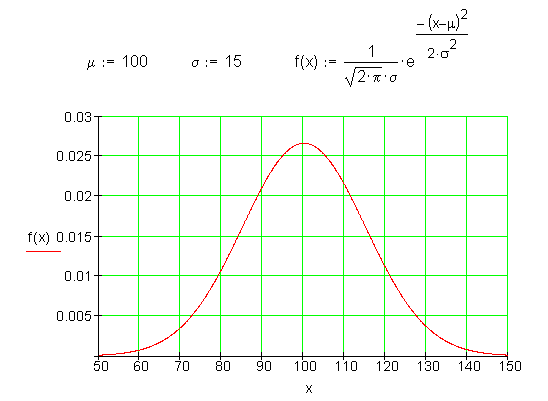
Die Transformation der x-Achse erfolgte hier linear mit der Transformationsformel.

Vorerst gehen wir hier nicht weiter auf die Parameter ein, das geschieht im Zusammenhang mit der Wahrscheinlichkeitsrechnung.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differential- und Integralrechnung. Darin auch Links zur Theorie und zu weiteren Aufgaben.


