Hier findest du die Lösungen der Aufgaben Polynomgleichungen V mit Text- und Parameteraufgaben.
1. Welche Menge
Welche Menge muss man produzieren und zu einem Stückpreis von 2000 € verkaufen, damit man einen Gewinn von 1500 € erzielt?
Ausführliche Lösung
K(x) heißt Kostenfunktion und gibt an, welche Kosten bei der Produktion der Menge x eines Produktes entstehen.
E(x) heißt Erlösfunktion und gibt an, wie groß der Erlös ist, wenn die Menge x verkauft wird.
G(x) = E(x) – K(x) heißt Gewinnfunktion und gibt an, wie hoch der Gewinn ist, wenn die Menge x verkauft wird.
Lösungsansatz: G(x) = 1500
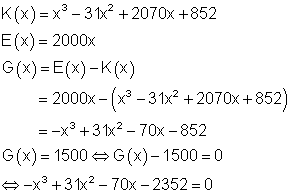
Die Polynomgleichung kann man lösen, wenn man die erste Lösung kennt. Um die erste Lösung zu finden, versucht man, ob ein Teiler vom Absolutglied, also von 2352 die Polynomgleichung erfüllt. Dazu bestimmt man zunächst die Teiler und setzt sie in das Horner-Schema ein.
Dazu kannst du dir das Video 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
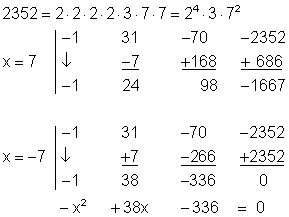
Wie das Horner-Schema zeigt, ist x = -7 eine Lösung der Polynomgleichung. Das Restpolynom ist eine quadratische Gleichung, die mit der p-q-Formel gelöst werden kann und damit weitere Lösungen liefert.
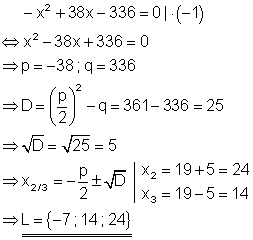
Für einen Gewinn von 1500 € mussen x = 14 bzw. x = 24 Stück verkauft werden. Die Lösung x = -7 hat für die Lösung keine Relevanz, da negativ. Negative Stückzahlen machen keinen Sinn.
2. Die Entwicklung der installierten Leistung von Windkraftanlagen
a)
Die Entwicklung der installierten Leistung von Windkraftanlagen in Deutschland seit 2006 lässt sich näherungsweise mit der Funktion
![]()
beschreiben.
Die Variable x steht für Jahre, P(x) für Gigawatt (GW).
Installierte Leistung an Windenergie in Deutschland laut BWE Bundesverband Windenergie:
![]()
Welche Leistung war 2006 installiert?
Ausführliche Lösung
Da das Jahr 2006 fur die Funktion als Startjahr gilt, bedeutet das für den x-Wertx = 0.
Setzt man diesen Wert in die Funktionsgleichung ein, dann gilt:
P(0) = 21. Das bedutet, im Jahr 2006 betrug die installierte Leistung etwa 21 Gigawatt.
2. b) Welche Leistung war 2013 installiert?
Ausführliche Lösung
Für 2013 muss die Differenz der Jahre zwischen 2006 und 20013 eingesetzt werden. Die Differenz beträgt x = 7.
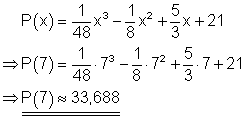
Im Jahr 2013 betrug die installierte Leistung etwa 33,688 GW. Der Wert lässt sich leicht mit dem Taschenrechner bestimmen.
2. c) In welchem Jahr kann unter gleichen Voraussetzungen mit einer installierten Leistung von 46 GW gerechnet werden?
Ausführliche Lösung. Ansatz:
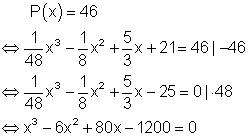
Um eine Lösung durch raten oder probieren zu finden, kann man entweder den Taschenrechner benutzen oder das Horner-Schema verwenden. Hat man eine Lösung für x z. B. mit dem Taschenrechner gefunden, so muss man auf jeden Fall die Polynomdivision durchführen um das Restpolynom zu finden. Hat man hingegen mit dem Horner-Schema einen Lösungswert für x gefunden, so lässt sich aus den Koeffizienten das Restpolynom bilden. Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision.
Durch raten erhält man die Lösung x = 10.
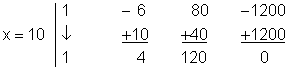
Da x = 10 eine Lösung der im Ansatz aufgestellten Polynomgleichung ist, beträgt die installierte Leistung im Jahre 2006 + 10 = 2016 etwa 46 GW.
Bemerkung:
Diese Rechnung ist lediglich eine Trendrechnung unter der Voraussetzung, das die Bedingungen sich für weitere Installationen nicht ändern. Politik und Wirtschaft können sowohl positiv, wie auch negativ diesen Trend beeinflussen.
3. Berechne!
a)
Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
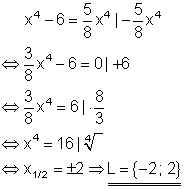
3. b) Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
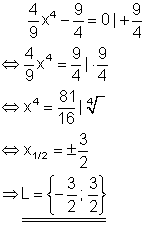
3. c) Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
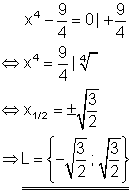
4. Berechne!
a)
Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
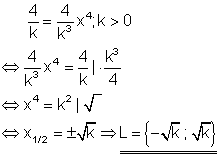
4. b) Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
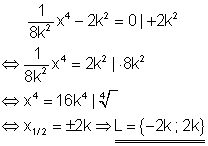
4. c) Berechne die Lösung folgender Gleichung!
Ausführliche Lösung
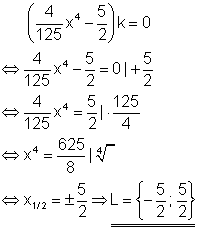
5. Berechne!
Für welche Werte von k gibt es eine Lösung?
Ausführliche Lösung

Wenn es eine Lösung geben soll, muss k > 0 sein, da die 4. Wurzel nur für positive Zahlen definiert ist.
6. Berechne!
Für welche Werte von k lässt sich die Gleichung lösen?
Ausführliche Lösung
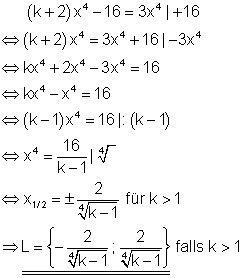
Da der Nenner des Bruches ungleich 0 und der Wert, der unter der 4. Wurzel steht positiv sein muss, gilt k > 1.
7. Berechne!
a)
Dagobert erbt 10.000 €. Er möchte das Kapital in 8 Jahren verdoppeln.
Wie hoch müsste die jährliche Verzinsung sein?
Ausführliche Lösung
Die Zinseszinsformel:
![]()
K0 : Anfangskapital
Kn : Guthaben nach n Jahren
p : Zinssatz in %
q = 1 + p/100 (Zinsfaktor)
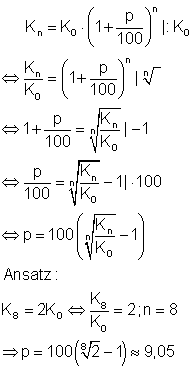
Die jährliche Verzinsung müsste etwa 9,09% betragen.
7. b) Welches Guthaben hätte er nach 15 Jahren?
Ausführliche Lösung
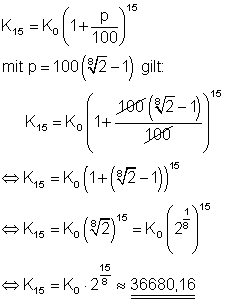
Nach 15 Jahren wäre das Kapital auf 36680,16 € angewachsen.
Eine Rechnung mit dem Näherungswert von p = 9,05% ergäbe 36878,57 €. Um den zu berechnenden Wert möglicht genau zu bekommen, setzt man für p den algebraischen Ausdruck ein und vereinfacht die Gleichung bevor man mit dem Taschenrechner das Ergebnis berechnet.
7. c) Wegen einer Finanzkriese vermehrt sich das Kapital in 8 Jahren nur auf 15000 €. Wie hoch war der mittlere Jahreszins?
Ausführliche Lösung
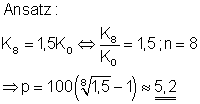
Der mittlere Jahreszins betrug etwa 5,2%.
8. Wie hoch ist die durchschnittliche jährliche Inflationsrate,
Wie hoch ist die durchschnittliche jährliche Inflationsrate, wenn das Geld innerhalb von 5 Jahren 12% an Kaufkraft verliert?
Ausführliche Lösung
Bei einer exponentiellen Abnahme gilt:
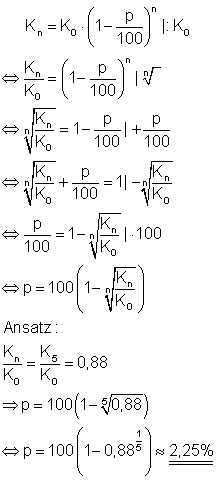
Die durchschnittliche jährliche Inflationsrate beträgt etwa 2,52%.
9. Löse die Gleichungen nach x auf!
a)
Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x3 ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden, der da lautet: „Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist“. Die Lösung der Gleichung findet man also dadurch, dass man jeden Faktor für sich gleich Null setzt.
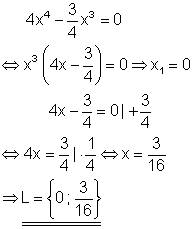
9. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x2 ausgeklammert werden.
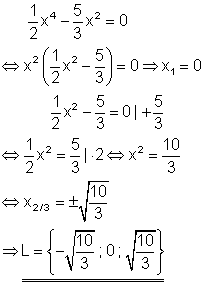
9. c) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x2 ausgeklammert werden.
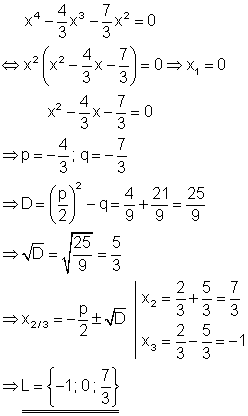
10. Löse die Gleichungen nach x auf!
a)
Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x ausgeklammert werden.
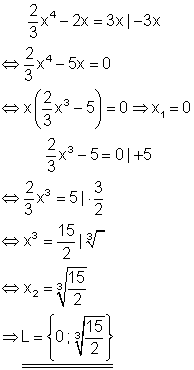
10. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x3 ausgeklammert werden.
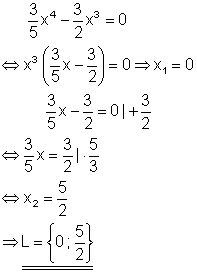
10. c) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x2 ausgeklammert werden.
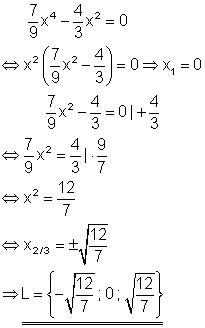
Hier findest du die Aufgaben.
und Aufgaben Polynomgleichungen VII.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

