In diesem Beitrag findet ihr ausführliche Lösungen zu vermischte Aufgaben mit Polynomgleichungen VII. Z. B.: Welche Anzahl an Lösungen sind möglich?
Dabei hilft dir sicher eins dieser Videos Playlist aller Videos zu Polynomgleichungen.
1. a) Ausführliche Lösung
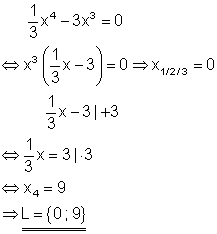
Aus der Polynomgleichung kann x3 ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden, der da lautet: „Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.“ Die Lösung der Gleichung findet man also dadurch, dass man jeden Faktor für sich gleich Null setzt. Der erste Faktor ergibt die dreifache Lösung 0. Der zweite Faktor ist eine lineare Gleichung, die durch Äquivalenzumformung zu lösen ist. In der Lösungsmenge erscheint die dreifache 0 nur einmal, da in der Mengendarstellung per Definition jedes Element nur einmal vorkommen darf.
1. b) Ausführliche Lösung
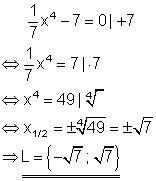
1. c) Ausführliche Lösung
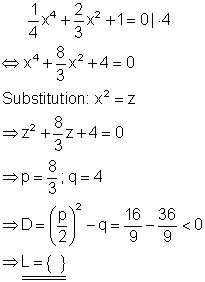
Die Polynomgleichung stellt eine biquadratische Gleichung dar. Die Substitutionsvariable z lässt sich mithilfe der p-q-Formel berechnen. Anschließend muss zurücksubstituiert und die Wurzel gezogen werden. Die Wurzel lässt sich nur für positive z-Werte lösen. Da in diesem Fall die Diskriminante < 0 ist, gibt es für z keine Lösung und damit auch keine für x.
2. a) Ausführliche Lösung
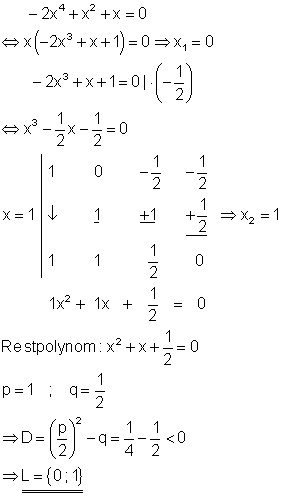
Um eine Lösung der Polynomgleichung durch raten oder probieren zu finden, kann man entweder den Taschenrechner benutzen oder das Horner-Schema verwenden. Hat man eine Lösung für x z. B. mit dem Taschenrechner gefunden, so muss man auf jeden Fall die Polynomdivision durchführen um das Restpolynom zu finden. Hat man hingegen mit dem Horner-Schema einen Lösungswert für x gefunden, so lässt sich aus den Koeffizienten das Restpolynom bilden. Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision. Durch raten und probieren erhält man die Lösung x = 1. Da die Diskriminante der quadratischen Gleichung kleiner Null ist, hat diese keine Lösung. Zu den bisher bekannten Lösungen kommt keine mehr hinzu.
Dazu kannst du dir das 📽️ Video Horner-Schema ersetzt Polynomdivision ansehen.
2. b) Ausführliche Lösung
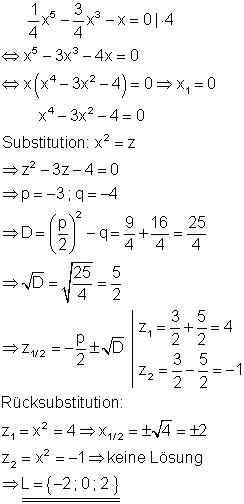
Die Polynomgleichung stellt eine biquadratische Gleichung dar. Die Substitutionsvariable z lässt sich mithilfe der p-q-Formel berechnen. Anschließend muss zurücksubstituiert und die Wurzel gezogen werden. Die Wurzel lässt sich nur für positive z-Werte lösen. Da z2 negativ ist, trägt nur die Wurzel aus z1 zur Lösung bei.
2. c) Ausführliche Lösung
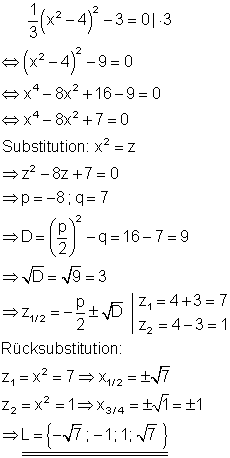
3. a) Ausführliche Lösung
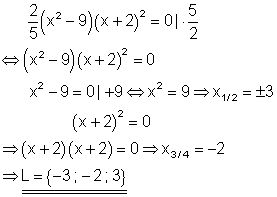
3. b) Ausführliche Lösung
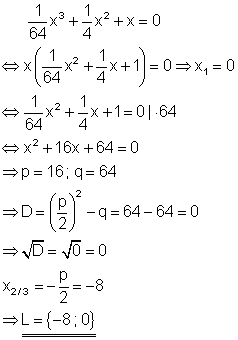
Da die Diskriminante D = 0 ist, gibt es für die quadratische Gleichung nur eine (doppelte) Lösung.
3. c) Ausführliche Lösung
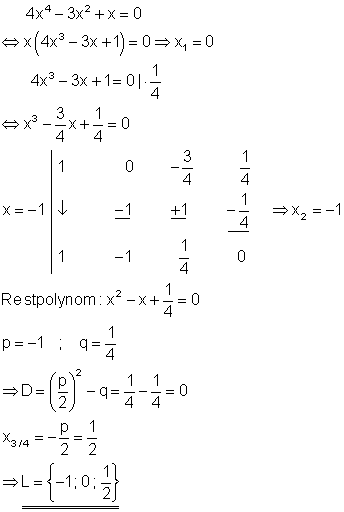
Durch raten und probieren erhält man die Lösung x = -1. Da die Diskriminante D = 0 ist, gibt es für die quadratische Gleichung nur eine (doppelte) Lösung.
4. a) Ausführliche Lösung
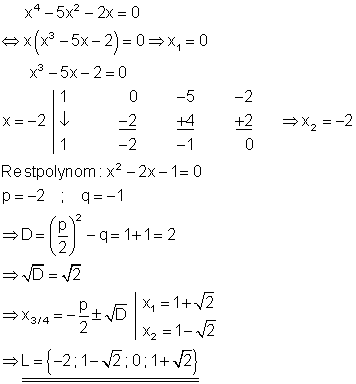
Durch raten und probieren erhält man die Lösung x = -2. Da die Diskriminante D > 0 ist, gibt es für die quadratische Gleichung zwei Lösungen. Mit den vorigen sind es dann 4 Lösungen. Raten führt oft zum Ziel, wenn man einen Teiler vom Absolutglied (hier = -2) nimmt.
4. b) Ausführliche Lösung
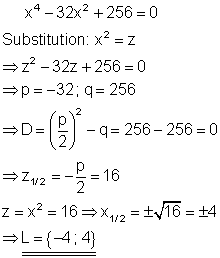
4. c) Ausführliche Lösung
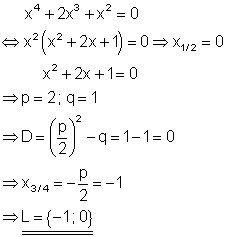
5. a) Ausführliche Lösung
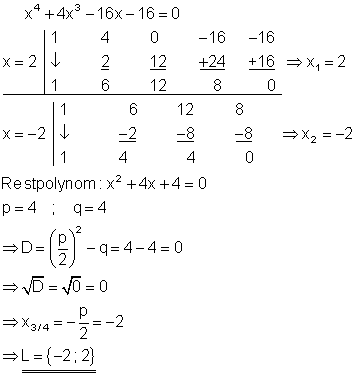
Durch raten und probieren erhält man die Lösung x = 2 und x = -2. Da die Diskriminante D = 0 ist, gibt es für die quadratische Gleichung nur eine doppelte Lösung x = -2. Diese Lösung war bereits schon vorhanden, so dass durch die Lösung der quadratischen Gleichung keine mehr dazu kommt.
5. b) Ausführliche Lösung
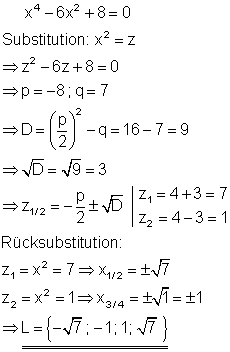
5. c) Ausführliche Lösung
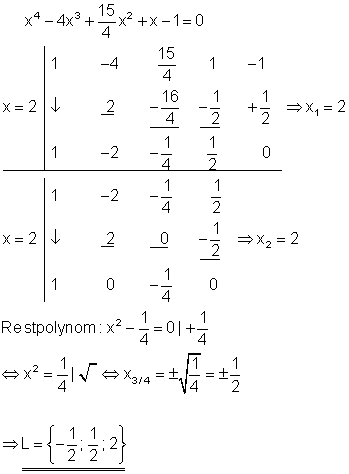
6. a) Ausführliche Lösung
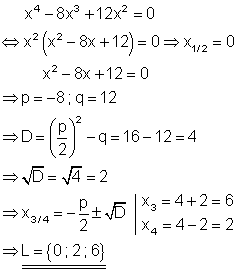
6. b) Ausführliche Lösung
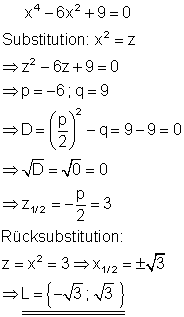
6. c) Ausführliche Lösung
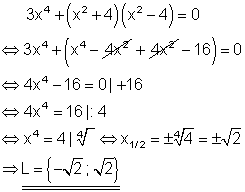
7. a) Ausführliche Lösung
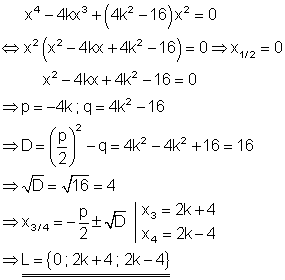
7. b) Ausführliche Lösung
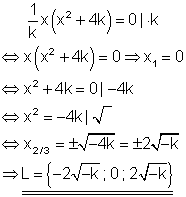
Da per Definition k negativ sein soll, ist -k immer positiv, so dass die Wurzel gezogen werden kann.
7. c) Ausführliche Lösung
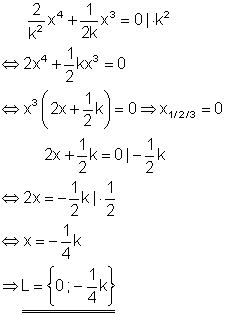
8. a) Ausführliche Lösung
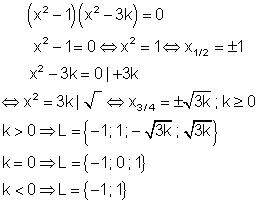
Falls k positiv ist, gibt es 4 Lösungen. Für k = 0 gibt es drei Lösungen da die Wurzel 0 ist. Für negative Werte von k gibt es zwei Lösungen da die Wurzel nicht lösbar ist.
8. b) Ausführliche Lösung
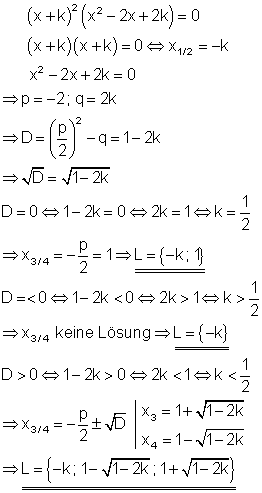
Die Lösungen sind von der Formvariablen k abhängig. Die Diskriminante D gibt Auskunft über die speziellen Werte von k für die es entweder eine, zwei oder drei Lösungen gibt.
9. Ausführliche Lösung
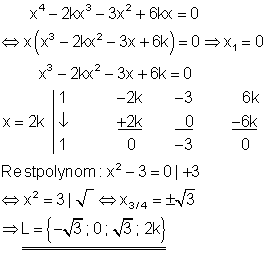
Der Satz vom Nullprodukt wird angewendet. Mit dem Horner-Schema und der bekannten Lösung x = 2k wird das Restpolynom bestimmt und daraus die weiteren Lösungen.
10. Ausführliche Lösung
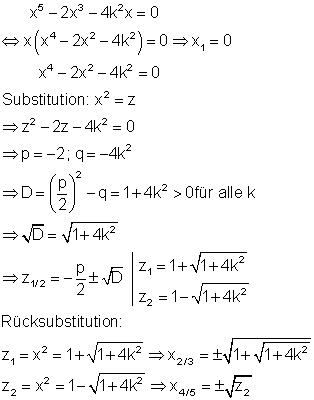
Die Wurzel aus z2 ist nur dann lösbar, wenn z2 größer oder gleich Null ist.
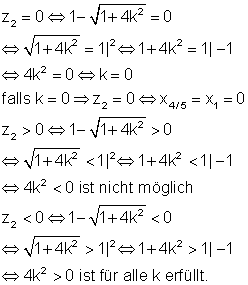
Die Polynomgleichung hat immer drei Lösungen. x1 =0 und x2/3 = Wurzel aus z1 existieren für alle Werte von k. Zu untersuchen ist, ob x4/5 = Wurzel aus z2 existiert. Falls z2 = 0 ist, gilt x4/5 = x1 = 0, also keine neue Lösung. Für den Fall z2 größer Null gäbe es weitere Lösungen. Die Rechnung zeigt, dass z2 nicht größer als Null sein kann. Deshalb gibt es außer den drei vorhandenen, keine weitere Lösung.
11. Ausführliche Lösung
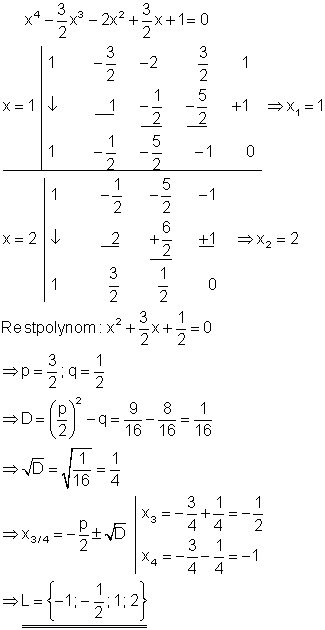
Hier findest du die Aufgaben.
Außerdem hier weitere Aufgaben Polynomgleichungen IV mit Parametern.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

