Hier findest du die Lösungen der vermischten Aufgaben zu quadratischen Gleichungen III mit komplettem Lösungsweg.
Dabei können dir diese Videos helfen: Playlist aller Videos zu quadratischen Gleichungen .
1. Ausführliche Lösungen
a)
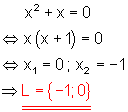
Lösung durch ausklammern und dem Satz vom Nullprodukt.
b)
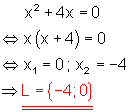
Lösung durch ausklammern und dem Satz vom Nullprodukt.
c)
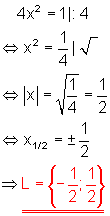
Lösung durch Wurzelziehen.
d)
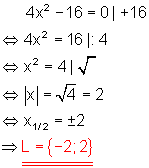
Lösung durch Wurzelziehen.
e)
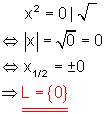
Lösung durch Wurzelziehen.
f)
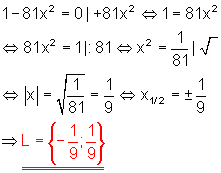
Lösung durch Wurzelziehen.
2. Ausführliche Lösungen
a)
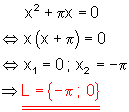
Lösung durch ausklammern und dem Satz vom Nullprodukt.
b)
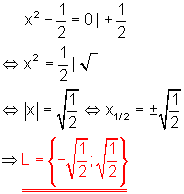
Lösung durch Wurzelziehen.
c)
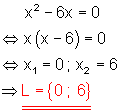
Lösung durch ausklammern und dem Satz vom Nullprodukt.
d)
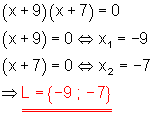
Lösung mit dem Satz vom Nullprodukt.
e)
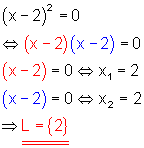
Lösung mit dem Satz vom Nullprodukt. Doppelte Nullstelle.
f)
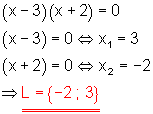
Lösung mit dem Satz vom Nullprodukt.
3. Ausführliche Lösungen
a)
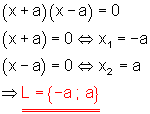
Lösung mit dem Satz vom Nullprodukt.
b)
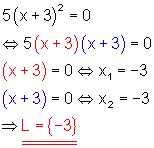
Lösung mit dem Satz vom Nullprodukt. Doppelte Nullstelle.
c)
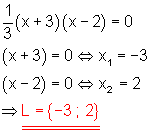
Lösung mit dem Satz vom Nullprodukt.
d)
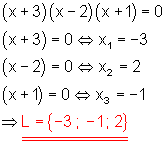
Lösung mit dem Satz vom Nullprodukt.
e)
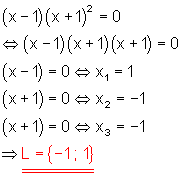
Lösung mit dem Satz vom Nullprodukt. Mit doppelter Nullstelle.
f)
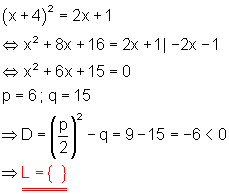
Bei negativer Diskriminante keine Lösung der quadratischen Gleichung.
4. Ausführliche Lösungen:
a)
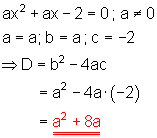
b)
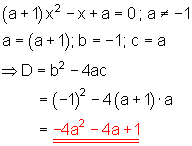
c)
\frac{a^2}{2}x^2 -4x = x^2 - ax +1; a \neq 0 | -x^2 \\
\Leftrightarrow \frac{a^2}{2}x^2 - x^2 - 4x = -ax +1 | +ax \\
\Leftrightarrow (\frac{a^2}{2} -1)x^2 -4x +ax
= 1 | -1
\Leftrightarrow (\frac{a^2}{2} -1)x^2 + (a - 4)x - 1 \\
a = (\frac{a^2}{2} -1) ; b = (a - 4) ; c = - 1 \\
\Rightarrow D = b^2 - 4ac = (a - 4)^2 - 4(\frac{a^2}{2} -1) \cdot (-1) \\
= a^2 - 8a + 16 + 2a^2 - 4 = \\
= \color{red}{\underline{\underline{3a^2 - 8a + 12}}}
d)
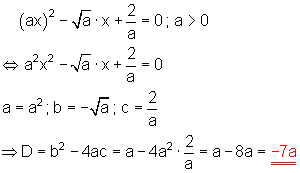
5. Ausführliche Lösung:
mx^2 + ax - 1 = 0
Jetzt müssen wir zeigen, dass die Diskriminante für alle a ∈ ℝ > 0 ist.
p = a ; q = -1 \Rightarrow D = (\frac{p}{2})^2 - q = \\
= \frac{a^2}{4} + 1 > 0 \Rightarrow zwei \quad Lösungen.
x_{1/2} = -\frac{p}{2} \pm \sqrt D = -\frac{a}{2} \pm \sqrt {\frac{a^2}{4} + 1}
\Rightarrow \color{red}{\underline{\underline{L = \{-\frac{a}{2} + \sqrt {\frac{a^2}{4} + 1} ; -\frac{a}{2} - \sqrt {\frac{a^2}{4} + 1} \}}}}
6. Ausführliche Lösungen:
a)
-ax^2 + 2ax - a + 1 = 0 ; a > 0
-ax^2 + 2ax - a + 1 = 0 | : (-a) \\
\Leftrightarrow x^2 - 2x + 1 - \frac{1}{a} = 0 \\
p = -2 ; q = 1 - \frac{1}{a}
\Rightarrow D = (\frac{p}{2})^2 - q \\
= 1 - (1 - \frac{1}{a}) = 1 - 1 + \frac{1}{a} = \frac{1}{a} \\
\Rightarrow \sqrt D = \sqrt{\frac{1}{a}}
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = 1 + \sqrt{\frac{1}{a}} \\
x_2 = 1 - \sqrt{\frac{1}{a}} \\
\Rightarrow \color{red}{\underline{\underline{L = \{1 + \sqrt{\frac{1}{a}} ; 1 - \sqrt{\frac{1}{a}}\}}}}
b)
x^2 - 2ax - 6a = -3x | +3x
\Leftrightarrow x^2 - 2ax - 6a + 3x = 0 \\
\Leftrightarrow x^2 - 2ax + 3x - 6a
= 0 \\
\Leftrightarrow x^2 - (2a - 3) \cdot x - 6a = 0 \\
\Rightarrow p = -(2a - 3) = 3 - 2a ; q = -6a \\
\Rightarrow D = (\dfrac{p}{2})^2 - q = (\dfrac{3 - 2a}{2})^2 + 6a \\
= \dfrac{9 - 12a + 4a^2}{4} +6a \\
= \dfrac{9 - 12a + 4a^2}{4}
+ \dfrac{24a}{4} \\
= \dfrac{9 - 12a + 4a^2 + 24a}{4} \\
= \dfrac{4a^2 + 12a
+ 9}{4} \\
= \dfrac{(2a + 3)^2}{4} \\
= (\frac{2a + 3}{2})^2 \\
\Rightarrow \sqrt D = \sqrt {(\frac{2a + 3}{2})^2} = \frac{2a + 3}{2}
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = \frac{2a - 3}{2} + \frac{2a + 3}{2} \\
= \frac{2a - 3 + 2a + 3}{2} = \frac{4a}{2} = 2a
x_2 = \frac{2a - 3}{2} - \frac{2a + 3}{2} \\
= \frac{2a - 3 - 2a - 3}{2} = \frac{-6}{2} = -3
\color{red}{\underline{\underline{L = \{-3 ; 2a\}}}}
c)
-ax^2 + 2a^2 + 3a^3 = 0 | : (-a) \\
\Leftrightarrow x^2 - 2ax - 3a^2 = 0 \\
\Rightarrow p = -2a ; q = -3a^2 \\
\Rightarrow D = (\frac{p}{2})^2 - q
= a^2 + 3a^2 = 4a^2
\Rightarrow \sqrt D = \sqrt{4a^2} = 2a
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = a + 2a = 3a \\
x_2 = a - 2a = -a \\
\Rightarrow \color{red}{\underline{\underline{L = \{-a ; 3a\}}}}
d)
-x^2 + 1,5ax - 0,5a^2 = 0 | : (-1) \\
\Leftrightarrow x^2 - \frac{3}{2}ax + \frac{1}{2}a^2 = 0\\
\Rightarrow p = -\frac{3}{2}a ; q = \frac{1}{2}a^2 \\
\Rightarrow D = (\frac{p}{2})^2 - q
= \frac{9}{16}a^2 - \frac{8}{16}a^2 = \frac{1}{16}a^2
\Rightarrow \sqrt D = \sqrt{\frac{1}{16}a^2} = \frac{1}{4}a
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = \frac{3}{4}a + \frac{1}{4}a = \frac{4}{4}a = a \\
x_2 = \frac{3}{4}a - \frac{1}{4}a = \frac{2}{4}a = \frac{1}{2}a \\
\Rightarrow \color{red}{\underline{\underline{L = \{\frac{1}{2}a ; a\}}}}
e)
-\frac{1}{a}(x^2 - 5x) = 0 ; a \neq 0 x ausklammern.
\Leftrightarrow -\frac{1}{a} x (x - 5) = 0 Diesmal wenden wir den Satz vom Nullprodukt an.
-\frac{1}{a} x = 0 \Leftrightarrow x_1 = 0 \\
x - 5 = 0 | + 5 \Leftrightarrow x_2 = 5 \\
\Rightarrow \color{red}{\underline{\underline{L = \{0 ; 5 \}}}}
f)
\frac{x^2}{3} - \frac{2}{3}ax - a^2 = 0 | \cdot 3 \\
\Leftrightarrow x^2 - 2ax - 3a^2 = 0 \\
\Rightarrow p = -2a ; q = -3a^2 \\
\Rightarrow D = (\frac{p}{2})^2 - q
= a^2 + 3a^2
\Rightarrow \sqrt D = \sqrt{4a^2} = 2a
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = a + 2a = 3a \\
x_2 = a - 2a = -a \\
\Rightarrow \color{red}{\underline{\underline{L = \{-a ; 3a\}}}}
7. Ausführliche Lösungen:
a)
2x^2 + x - 3a = 0 | : 2 \\
\Leftrightarrow x^2 + \frac{1}{2} x - \frac{3}{2}a = 0
\Rightarrow p = \frac{1}{2} ; q = -\frac{3}{2}a \\
\Rightarrow D = (\frac{p}{2})^2 - q = \frac{1}{16} + \frac{3}{2}a \\
= \frac{1}{16} + \frac{24}{16}a = \frac{1}{16} (24a + 1)
Da die Diskriminante von a abhängt, müssen wir eine Fallunterscheidung durchführen.
Für D > 0 gibt es 2 Lösungen.
Die Bedingung für a ist dann:
D > 0 \Leftrightarrow \frac{1}{16} (24a + 1) > 0 | \cdot 16
\Leftrightarrow 24a + 1 > 0 | -1 \\
\Leftrightarrow 24a
> -1 | :24 \\
\Leftrightarrow 24a
> -1 | :24 \\
\Leftrightarrow a > -\frac{1}{24} \\
\sqrt D = \sqrt { \frac{1}{16}(24a + 1) } = \frac{1}{4} \sqrt { 24a +1}
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = -\frac{1}{4} + \frac{1}{4}\sqrt { 24a +1} \\
x_2 = -\frac{1}{4} - \frac{1}{4}\sqrt { 24a +1} \\
\Rightarrow \color{red}{\underline{\underline{L = \{ -\frac{1}{4} + \frac{1}{4}\sqrt { 24a +1} : -\frac{1}{4} - \frac{1}{4}\sqrt { 24a +1} \}}}}
Für D = 0 gibt es eine Lösung.
Die Bedingung für a ist dann:
a = - \frac{1}{24} \Rightarrow x_{1/2} = -\frac{p}{2}
= -\frac{1}{4} \Rightarrow \color{red}{\underline{\underline{L = \{ -\frac{1}{4} \}}}}
Für D < 0 gibt es keine Lösung.
Die Bedingung für a ist dann:
a < - \frac{1}{24} \Rightarrow \color{red}{\underline{\underline{L = \{ \}}}}
b)
ax^2 + 2x - 3 = 0 | :a \\
\Leftrightarrow x^2 + \frac{2}{a}x - \frac{3}{2} = 0
\Rightarrow p = \frac{2}{a} ; q = -\frac{3}{a} \\
\Rightarrow D = (\frac{p}{2})^2 - q = \frac{1}{a^2} + \frac{3}{a} \\
= \frac{1}{a^2} + \frac{3a}{a^2} = \frac{1}{a^2}(3a + 1)
Für D > 0 gibt es zwei Lösungen.
D > 0 \Leftrightarrow \frac{1}{a^2}(3a + 1) > 0 | \cdot a^2 \\
\Leftrightarrow 3a + 1 > 0 | -1 \\
\Leftrightarrow 3a > -1
| :3
\Leftrightarrow a > - \frac{1}{3}
\sqrt D = \sqrt { \frac{1}{a^2}(3a + 1) }
=\frac{1}{a} \sqrt {3a + 1}
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = -\frac{1}{a} + \frac{1}{a}\sqrt {3a + 1} \\
x_2 = -\frac{1}{a} - \frac{1}{a}\sqrt {3a + 1} \\
\Rightarrow \color{red}{\underline{\underline{L = \{-\frac{1}{a} + \frac{1}{a}\sqrt {3a + 1} ; -\frac{1}{a} - \frac{1}{a}\sqrt {3a + 1} \}}}}
Für D = 0 gibt es eine Lösung.
Die Bedingung für a ist dann:
a = -\frac{1}{3} \Rightarrow x_{1/2} = -\frac{p}{2} = -\frac{1}{a} \Rightarrow \color{red}{\underline{\underline{L = \{-\frac{1}{a}\} }}}
Für D < 0 gibt es keine Lösung. Die Bedingung für a ist dann:
a < -\frac{1}{3} \Rightarrow \color{red}{\underline{\underline{L = \{ \} }}}
c)
x^2 -ax + a = x | -x \\
\Leftrightarrow x^2 -ax - x + a = 0
\Leftrightarrow x^2 - (a + 1)x + a = 0 \\
\Rightarrow D = (\frac{p}{2})^2 - q = (\frac{a + 1}{2})^2 - a \\
= \frac{a^2 + 2a + 1}{4} - \frac{4a}{4} = (\frac{a - 1}{2})^2
Für D > 0 gibt es 2 Lösungen:
D > 0 \Leftrightarrow (\frac{a - 1}{2})^2 > 0
Die Bedingung ist erfüllt für alle a \neq 1 \\
\sqrt D = \sqrt {( \frac{a - 1}{2}) }^2 = \frac{a - 1}{2} = \frac{1}{2}(a - 1)
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = \frac{1}{2}(a + 1) + \frac{1}{2}(a - 1) \\
= \frac{1}{2}a + \frac{1}{2} + \frac{1}{2}a - \frac{1}{2} = a \\
x_2 = \frac{1}{2}(a + 1) - \frac{1}{2}(a - 1) \\
= \frac{1}{2}a + \frac{1}{2} - \frac{1}{2}a + \frac{1}{2} = 1 \\
\Rightarrow \color{red}{\underline{\underline{L = \{a ; 1 \}}}}
Für D = 0 gibt es eine Lösung.
Die Bedingung für a ist dann:
a = 1 \Rightarrow x_{1/2} = -\frac{p}{2} \\
= \frac{1}{2}(a + 1) = \frac{1}{2}(1 + 1) = 1 \Rightarrow \color{red}{\underline{\underline{L = \{ 1 \}}}}
Diese Lösung ist bereits in der Lösung für D > 0 enthalten.
8. Ausführliche Lösung
x^2 - 2x +3k - 1 = 0
Zu zeigen ist, dass für k ≤ \frac{2}{3} \quad L = \{ 1 + \sqrt {2 - 3k} ; 1 - \sqrt {2 - 3k} \} gilt:
p = -2 ; q = 3k - 1 \\
\Rightarrow D = (\frac{p}{2})^2 - q = 1 - (3k - 1) = 1 - 3k + 1 = 2 - 3k
x_{1/2} = -\frac{p}{2} \pm \sqrt D = 1 \pm \sqrt{2 - 3k}
Da der Radikant D ≥ 0 sein muss, müssen wir prüfen, für welche Werte von k das der Fall ist.
D ≥ 0 \Leftrightarrow 2 - 3k ≥ 0 | -2 \\
\Leftrightarrow -3k ≥ -2 | : (-3) \\
\Leftrightarrow k ≤ \frac{2}{3} \\
\Rightarrow \color{red}{\underline{\underline{L = \{1 + \sqrt{2 - 3k} ; 1 - \sqrt{2 - 3k} \}}}} \quad für \quad k ≤ \frac{2}{3}
9. Ausführliche Lösung
x^2 - 5x + k = 0
Als erstes setzen wir x = k in die Gleichung ein:
k^2 - 5k + k = 0 \\
\Leftrightarrow k^2 - 4k = 0 \\
\Leftrightarrow k(k - 4) = 0
Als nächstes wenden wir den Satz vom Nullprodukt an:
\Rightarrow k_1 = 0 ; k - 4 = 0 \Leftrightarrow k_2 = 4 \\
\Rightarrow \color{red}{\underline{\underline{L = \{0 ; 4 \}}}}
10. Ausführliche Lösung
x^2 - 2x - k^2 \Rightarrow p = -2 ; q = -k^2
\Rightarrow D = (\frac{p}{2})^2 - q \\
= 1 + k^2 = k ^2 + 1 \\
\Rightarrow \sqrt D = \sqrt{k^2 + 1} > 0 für alle k ∈ ℝ.
Die Lösungen sind:
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = 1 + \sqrt{k^2 + 1} \\
x_2 = 1 - \sqrt{k^2 + 1} \\
\Rightarrow \color{red}{\underline{\underline{L = \{1 + \sqrt{k^2 + 1} ; 1 - \sqrt{k^2 + 1} \quad für \quad alle \quad k \in \mathbb{R} \}}}} .
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie hier: Quadratische Gleichungen und p-q-Formel
und Zusammenfassung Quadratische Funktionen.
Hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.

