Wenn ihr viele Aufgaben mit den Lösungen zur relativen Häufigkeit in der Wahrscheinlichkeitsrechnung übt, werdet ihr gut in Mathe! Deshalb stelle ich hier auch den kompletten Lösungsweg zur Verfügung.
1.
Über die Zusammensetzung der Schülerschaft eines Gymnasiums ist bekannt:
In der Sek. I befinden sich 340 Jungen und 320 Mädchen. In der Sek. II befinden sich 150 Jungen und 190 Mädchen.
a) Stelle eine Vierfeldtafel auf und berechne die relativen Häufigkeiten.
b) Mit welcher Wahrscheinlichkeit ist ein zufällig ausgewählterSchüler/in in der Sek. I?
c) Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person in der Sek. II und ein Mädchen?
1. Ausführliche Lösungen
a)
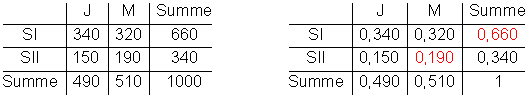
b) ![]()
c) ![]()
2.
Gewinnwahrscheinlichkeit und Gewinnchancen.
a) Bei einem Zufallsversuch sind die Chancen für einen Gewinn:
(1) 1 zu 3 (2) 1 zu 1 (3) 2 zu 3 (4) 4 zu 3 (5) a zu b.
Wie groß ist jeweils die Gewinnwahrscheinlichkeit in den genannten Fällen?
b) Die Wahrscheinlichkeit für einen Gewinn ist:
![]()
Wie stehen in jedem einzelnen Fall die Chancen?
2. Ausführliche Lösungen
a) Unter der Gewinnchance 1 zu 3 kann man sich ein Urnenexperiment vorstellen. In der Urne befinden sich 1 rote Kugel (Gewinn) und 3 schwarze Kugeln (Nieten). Es wird nun einmal gezogen. Die Wahrscheinlichkeit eine rote Kugel zu ziehen ist in diesem Fall 0,25.

b)

3.
In einer Urne befinden sich drei schwarze, sieben blaue und sechs rote Kugeln. Sven zieht eine Kugel.
a) Mit welcher Wahrscheinlichkeit ist diese Kugel rot oder blau?
b) Mit welcher Wahrscheinlichkeit ist diese Kugel schwarz oder rot?
c) Mit welcher Wahrscheinlichkeit ist diese Kugel nicht rot?
3. Ausführliche Lösungen
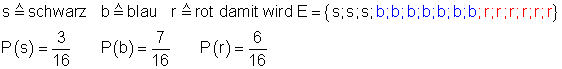
a)
![]()
b)
![]()
c)
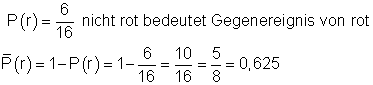
4.
Eine Umfrage an einer Schule mit insgesamt 1250 Schülerinnen und Schülerrat ergeben, dass 4,4 % der Mädchen und 6,4% der Jungen Nichtschwimmer sind. Insgesamt ergab sich ein Anteil von 5,2% Nichtschwimmern an der Schule.
a) Entwickele anhand der gegebenen Daten je eine Vierfeldtafel mit den absoluten und mit den relativen Häufigkeiten.
b) Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person ein Mädchen?
c) Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person ein Junge, der schwimmen kann?
d) Mit welcher Wahrscheinlichkeit ist eine zufällig ausgewählte Person ein Mädchen, das nicht schwimmen kann?
4. Ausführliche Lösungen
a)

b) P (A) = 0,6 ist die Wahrscheinlichkeit dafür, bei einer zufälligen Auswahl ein Mädchen zu wählen.
c) P (B) = 0,3744 ist die Wahrscheinlichkeit dafür, bei einer zufälligen Auswahl einen Jungen zu wählen, der schwimmen kann.
d) P (C) = 0,0264 ist die Wahrscheinlichkeit dafür, bei einer zufälligen Auswahl ein Mädchen zu wählen, das nicht schwimmen kann.
5.
In einer Urne befinden sich 3 rote, 5 grüne und 4 schwarze Kugeln. Es wird eine Kugel gezogen.
Folgende Ereignisse sind definiert:
A: Es wird eine grüne Kugel gezogen.
B: Es wird eine rote Kugel gezogen.
C: Die gezogene Kugel ist nicht grün.
D: Die gezogene Kugel ist nicht rot.
E: Die gezogene Kugel ist weder grün noch ist sie rot.
a) Berechne die Wahrscheinlichkeiten aller Ereignisse.
b) Berechne die Wahrscheinlichkeit der oder Verknüpfung der Ereignisse A und B. Wie lautet dieses Ereignis in Textform?
c) Berechne die Wahrscheinlichkeit des Gegenereignisses von E. Wie lautet dieses Ereignis in Textform?
5. Ausführliche Lösungen
a)
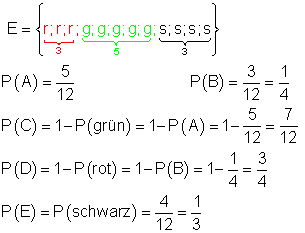
b)
![]()
Ereignistext: Die gezogene Kugel ist grün oder rot.
c)
![]()
Ereignistext: Die gezogene Kugel ist nicht schwarz.
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

