Hier findet ihr die Lösungen der Aufgaben zu Zählstrategien Kombinatorik II. Darin müsst ihr berechnen, wie groß die Wahrscheinlichkeit für bestimmte Ereignisse ist.
1. Aufgabe
Aus schwarzen und weißen Mühlsteinen werden Türme gebaut, indem immer acht Steine übereinander gestapelt werden. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse, wenn die Farbe jeweils zufällig gewählt wird?
A: Alle Steine haben dieselbe Farbe.
B: Nur ein Stein ist weiß.
C: Der erste und der letzte Stein haben dieselbe Farbe.
1. Ausführliche Lösungen
Modell: Geordnete Stichprobe mit Zurücklegen
Zwei Farben stehen für jeden der 8 Steine zur Verfügung .(8 mal ziehen mit Zurücklegen)
Die Anzahl der Möglichkeiten aller Farbkombinationen ist 28 = 256
A: Alle 8 Steine haben dieselbe Farbe.
Das bedeutet, entweder sind alle 8 Steine schwarz oder weiß.
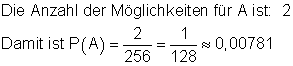
die Wahrscheinlichkeit dafür, dass alle Steine die gleiche Farbe haben.
B: Nur ein Stein ist weiß.
Da dieser Stein an jeder der insgesamt 8 Stellen liegen kann, gibt es dafür 8 Möglichkeiten.
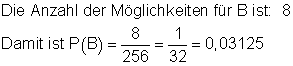
die Wahrscheinlichkeit dafür, dass von den 8 Steinen nur einer weiß ist.
C: Der erste und der letzte Stein haben dieselbe Farbe.
Für den ersten und letzten Stein gibt es 2 Möglichkeiten. Entweder beide weiß oder beide schwarz. Für die restlichen 6 Steine gibt es 26 Möglichkeiten.
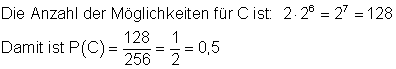
die Wahrscheinlichkeit dafür, dass der 1. und der letzte Stein dieselbe Farbe hat.
2. Aufgabe
In einer Tüte befinden sich 1 rotes, 2 grüne, 3 gelbe und 4 braune Gummibärchen. Jemand entnimmt drei Gummibärchen. Wie groß ist die Wahrscheinlichkeit für folgendes Ereignis?
A: Genau ein grünes Gummibärchen wird gezogen.
2. Ausführliche Lösung
Modell: Ungeordnete Stichprobe ohne Zurücklegen oder Ziehen mit einem Griff.
Die Anzahl der Möglichkeiten 3 Gummibärchen aus einer Tüte mit insgesamt 10 Gummibärchen zu ziehen ist:
![]()
A: Genau ein grünes Gummibärchen wird gezogen.
Die Anzahl der Möglichkeiten 1 grünes Gummibärchen von insgesamt 2 grünen zu ziehen und 2 Gummibärchen aus den insgesamt 8 andersfarbigen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von A. Damit ist
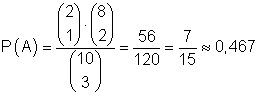
die Wahrscheinlichkeit dafür, genau ein grünes Gummibärchen zu ziehen.
3. Aufgabe
Für eine Variete-Veranstaltung stehen 5 Nummern zur Verfügung, darunter eine Jongliernummer. Die Reihenfolge des Programms wird ausgelost. Wie groß ist die Wahrscheinlichkeit folgender Ereignisse?
A: Die Jongliernummer steht an der 3. Stelle im Programm?
B: Die Jongliernummer steht nicht am Schluss.
3. Ausführliche Lösungen
A: Die Jongliernummer steht an 3. Stelle.
xxJxx Bei der Auslosung kann die Jongliernummer an jeder beliebigen Stelle vorkommen.
Modell: Urne mit 5 Kugeln nummeriert von 1 bis 5.
Die Zahlen geben die Stelle an, an der die Jongliernummer im Programm steht. Einmaliges Ziehen bestimmt die Stelle im Programm, an der die Jongliernummer kommt.
![]()
die Wahrscheinlichkeit dafür, dass die Jongliernummer an 3. Stelle kommt. Mit der gleichen Wahrscheinlichkeit käme sie an einer beliebigen anderen Stelle vor.
B: Die Jongliernummer steht nicht am Schluss.
Das bedeutet, sie kann an 1., 2., 3. oder 4. Stelle stehen. Nach dem Additionssatz für Wahrscheinlichkeiten gilt:
![]()
die Wahrscheinlichkeit dafür, dass die Jongliernummer nicht an letzter Stelle steht.
4. Aufgabe
In einer Packung sind 10 LED-Lampen, davon sind zwei defekt. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse, wenn drei LED-Lampen „blind“ herausgegriffen werden?
A: Alle drei LED-Lampen sind in Ordnung.
B: Genau eine Glühlampe ist defekt.
C: Genau zwei LED-Lampen sind defekt.
4. Ausführliche Lösungen
Modell: Ungeordnete Stichprobe ohne Zurücklegen
n = 10 LED-Lampen, davon sind 2 defekt. 3 LED-Lampen werden zufällig entnommen. Die Anzahl der Möglichkeiten aus einer Packung mit 10 LED-Lampen zufällig 3 auszuwählen ist:
![]()
A: Alle 3 LED-Lampen sind in Ordnung.
Die Anzahl der Möglichkeiten aus 8 heilen LED-Lampen 3 auszuwählen ist 3 aus 8.
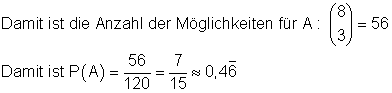
die Wahrscheinlichkeit dafür, drei heile LED-Lampen auszuwählen.
B: Genau eine Glühlampe ist defekt.
Von den 8 heilen LED-Lampen werden 2 und von den 2 defekten LED-Lampen wird eine gezogen.

die Wahrscheinlichkeit dafür, dass von den drei ausgewählten LED-Lampen eine defekt ist.
C: Genau zwei LED-Lampen sind defekt.
Von 8 heilen LED-Lampen wird eine und von den 2 defekten LED-Lampen werden 2 gezogen.
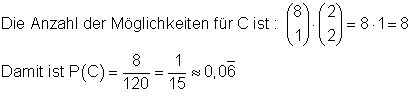
die Wahrscheinlichkeit dafür, dass von den drei ausgewählten LED-Lampen zwei defekt ist.
5. Aufgabe
Wie groß ist die Wahrscheinlichkeit, dass unter 8 Personen mindestens 2 Personen im selben Monat Geburtstag haben? Nehmen Sie näherungsweise an, dass alle Monate gleich lang sind.
A: Mindestens 2 der 8 Personen haben im selben Monat Geburtstag.
5. Ausführliche Lösung
Modell: Geordnete Stichprobe mit Zurücklegen
Die Anzahl der Möglichkeiten 8 Personen auf 12 Monate zu verteilen ist 128. (Ziehen mit Zurücklegen aus einer Urne mit 12 unterschiedlichen Kugeln)
A: Von 8 Personen haben mindestens 2 Personen im selben Monat Geburtstag.
Das Gegenereignis von A ist, alle 8 Personen haben in verschiedenen Monaten Geburtstag. Nun werden die 8 Personen so auf die 12 Monate verteilt, das es keine Dopplungen gibt.
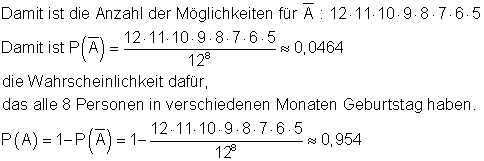
ist die Wahrscheinlichkeit dafür, dass von 8 Personen mindestens 2 im selben Monat Geburtstag haben.
6. Aufgabe
In einer Urne sind 6 rote, 5 blaue und 4 grüne Kugeln. 3 Kugeln werden auf einen Griff entnommen. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
A: Zwei grüne Kugeln wurden gezogen.
B: Unter den gezogenen Kugeln befindet sich keine grüne.
6. Ausführliche Lösungen
Modell: Ungeordnete Stichprobe ohne Zurücklegen oder Ziehen mit einem Griff.
Die Anzahl der Möglichkeiten 3 Kugeln aus einer Urne mit insgesamt 15 Kugeln zu ziehen ist:
![]()
A: Genau zwei grüne Kugeln werden gezogen.
Die Anzahl der Möglichkeiten 2 grüne Kugeln von insgesamt 4 grünen zu ziehen und eine andersfarbige aus den insgesamt 11 andersfarbigen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von A. Damit ist
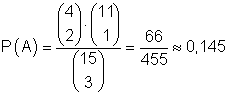
die Wahrscheinlichkeit dafür, genau zwei grüne Kugeln zu ziehen.
B: Keine grüne Kugel wird gezogen.
Die Anzahl der Möglichkeiten 0 grüne Kugeln von insgesamt 4 grünen zu ziehen und 3 andersfarbige aus den insgesamt 11 andersfarbigen zu ziehen ist:
![]()
Das ist die Anzahl der Möglichkeiten für das Eintreten von B.
Damit ist
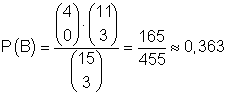
die Wahrscheinlichkeit dafür, keine grüne Kugel zu ziehen.
7. Aufgabe
Beim Spiel „Reise nach Jerusalem“ scheidet in jeder Runde eine Person aus. An dem Spiel nehmen 8 Personen teil. Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
A: Lars bleibt als letzter übrig.
B: Anja und Vanessa bestreiten die letzte Runde.
7. Ausführliche Lösungen
8 Personen nehmen an dem Spiel teil. Nach jeder Runde scheidet eine aus. Nach der ersten Runde gibt es 8 Möglichkeiten, nach der 2. Runde 7 Möglichkeiten usw. das jemand ausscheidet. Damit ist die Anzahl aller Möglichkeiten: 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 8! = 40.320.
A: Lars bleibt als letzter übrig.
xxxxxxxL Die Anzahl der Möglichkeiten 7 Personen auf 7 Plätze zu verteilen und Lars auf den letzten ist 7!
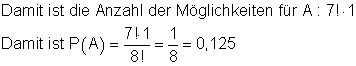
die Wahrscheinlichkeit dafür, dass Lars als letzter übrig bleibt.
B: Anja und Vanessa bestreiten die letzte Runde, mit den Anfangsbuchstaben dargestellt sieht dies so aus: xxxxxxxAV oder xxxxxxVA
Die Anzahl der Möglichkeiten 6 Personen auf 6 Plätze und 2 Personen auf 2 Plätze zu verteilen ist 6! mal 2!
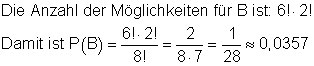
die Wahrscheinlichkeit dafür, dass Anja und Vanessa die letzte Runde bestreiten.
8. Aufgabe
Bei einem Multiple-Choice-Test gibt es 10 Fragen mit je drei möglichen Antworten, von denen jeweils genau eine richtig ist. Jemand kreuzt nach dem Zufallsprinzip bei jeder Frage eine Antwort an. Wie groß ist die Wahrscheinlichkeit der folgenden Ereignisse?
A: Alle Antworten sind falsch.
B: Die ersten 5 sind richtig, die letzten 5 sind falsch angekreuzt.
C: Genau die Hälfte der Antworten sind richtig.
D: 4 Antworten sind richtig, 6 sind falsch.
8. Ausführliche Lösungen 10 Fragen mit je 3 möglichen Antworten.
Die Anzahl der Möglichkeiten bei 10 Fragen jeweils eine von drei möglichen Antworten anzukreuzen ist 310. (Urne mit 3 verschiedenen Kugeln, 10 mal Ziehen mit Zurücklegen)
A: Alle Antworten sind falsch.
Bei jeder der 10 Fragen gibt es 2 Möglichkeiten falsch anzukreuzen.
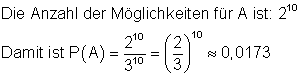
die Wahrscheinlichkeit dafür, alle Antworten falsch anzukreuzen.
B: Die ersten 5 Fragen sind richtig, die letzten 5 Fragen sind falsch angekreuzt.
Für die ersten 5 Fragen gibt es jeweils eine, für die zweiten 5 Fragen jeweils 2 Möglichkeiten anzukreuzen.
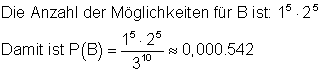
die Wahrscheinlichkeit dafür, die ersten 5 Fragen richtig angekreuzt zu haben.
C: Genau die Hälfte der Fragen sind richtig angekreuzt.

die Wahrscheinlichkeit dafür, genau die Hälfte der Fragen richtig zu beantworten.
D: 4 Antworten sind richtig, 6 sind falsch.

die Wahrscheinlichkeit dafür, 4 Fragen richtig angekreuzt zu haben.
9. Aufgabe
Die Buchstaben des Wortes ANANAS werden geschüttelt und neu geordnet. Wie groß ist die Wahrscheinlichkeit der folgenden Ereignisse?
A:Es entsteht wieder das Wort ANANAS.
B:Die Buchstabenkombination beginnt mit AAA.
C:Es entsteht ein Wort mit dreifachem A direkt hintereinander.
9. Ausführliche Lösungen ANANAS:
Die Anzahl der Möglichkeiten 6 Buchstaben anzuordnen ist 6!
A: Es entsteht wieder das Wort ANANAS.

die Wahrscheinlichkeit dafür, dass nach dem Schütteln wieder das Wort ANANAS entsteht.
B: Die Buchstabenkombination beginnt mit AAA.
AAAxxx

die Wahrscheinlichkeit dafür, dass nach dem Schütteln AAA die Anfangsbuchstaben bilden.
C: Es entsteht ein Wort mit dreifachem A direkt hintereinander.
AAAxxx oder xAAAxx oder xxAAAx oder xxxAAA
![]()
Ist die Wahrscheinlichkeit dafür, dass nach dem Schütteln ein Wort mit dreifachem A hintereinander entsteht.
Hier finden Sie die Aufgaben hierzu.
Und hier die Theorie: Kombinatorik.
Hier finden Sie eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

