Hier findet ihr die Lösungen der Aufgaben zur Kombinatorik III, auch Zählstrategie genannt. Diesmal ziehen wir Kärtchen mit einem Griff. Natürlich müsst ihr auch hier die Wahrscheinlichkeiten berechnen.
1.
In einer Urne befinden sich 14 gleich große Kärtchen, auf denen jeweils nur ein Buchstabe aufgedruckt ist.

Wir führen folgende Zufallsexperimente durch:
a) Wir nehmen mit einem Griff zwei Kärtchen aus der Urne.
Folgende Ereignisse sind definiert:
A: Die Buchstaben auf den beiden Kärtchen sind gleich.
B: Die zwei gezogenen Buchstaben sind Konsonanten.
Berechne die Wahrscheinlichkeiten für folgende Ereignisse:
![]()
b) Wir nehmen nacheinander fünf Kärtchen aus der Urne und legen sie der Reihe nach nebeneinander. Wie groß ist die Wahrscheinlichkeit dafür, dass das Wort TANNE entsteht?
c) Wir nehmen fünf Kärtchen mit einem Griff aus der Urne. Wie groß ist die Wahrscheinlichkeit, dass sich mit den gezogenen Buchstaben das Wort TANTE legen lässt?
d) Jens schlägt folgendes Spiel vor:
Aus der Urne werden mit einem Griff drei Kärtchen gezogen. Danach wird nach folgender Tabelle ausgezahlt:

Wie hoch muss der Einsatz sein, damit das Spiel fair ist?
e) Wir nehmen mit einem Griff zwei Kärtchen aus der Urne.
(1): Bestimme die Wahrscheinlichkeit dafür, das die gezogenen Buchstaben Vokale oder Konsonanten sind.
(2): Wie viel Kärtchen mit Konsonanten müssen wir zusätzlich in die Urne legen, damit die Wahrscheinlichkeit für das Ereignis unter(1) gleich 0,5 ist?
1. Ausführliche Lösungen
Die Urne enthält insgesamt 14 Buchstaben: 1 A; 4 E; 5 N; 1 O; 3 T
a)
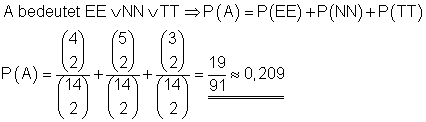
I. Die Wahrscheinlichkeit dafür, dass auf beiden Karten die Buchstaben gleich sind ist 0,209.
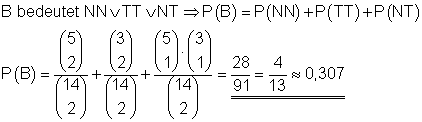
II. Die Wahrscheinlichkeit dafür, dass auf beiden Karten die Buchstaben Konsonanten sind ist 0,307.
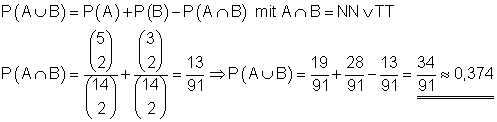
III. Die Wahrscheinlichkeit dafür, dass auf beiden Karten die Buchstaben gleich oder Konsonanten sind ist 0,374.
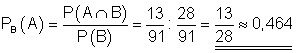
Wenn man weiß, dass die Buchstaben auf beiden Karten Konsonanten sind, dann ist die Wahrscheinlichkeit dafür, das es sich um gleiche Buchstaben handelt 0,464.
b) 5 Karten angeordnet bilden das Wort TANNE
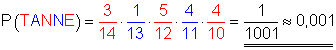
Die Wahrscheinlichkeit dafür, dass das Wort TANNE entsteht, ist etwa 0,001.
c) 5 Karten mit einem Griff.
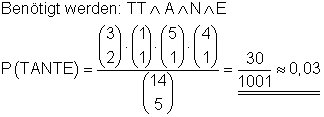
Die Wahrscheinlichkeit dafür, dass das Wort TANTE legen lässt, ist etwa 0,03.
d) Unter den 14 Buchstaben gibt es 6 Vokale und 8 Konsonanten.
Die Werte der Zufallsvariablen X sind:
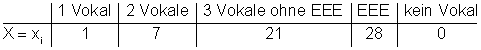
Deren Wahrscheinlichkeit ist:
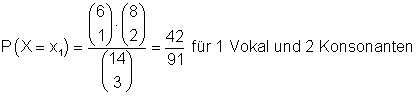
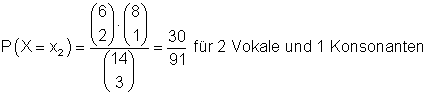
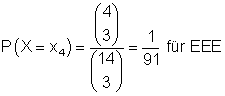
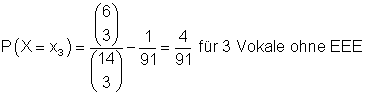
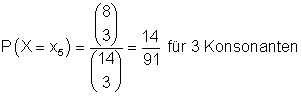
Wahrscheinlichkeiten der Zufallsvariablen und Berechnung des Erwartungswerts:
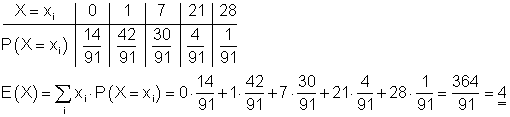
Bei einem Einsatz von 4 € ist das Spiel fair.
d) (1) 6 Vokale und 8 Konsonanten befinden sich in der Urne.
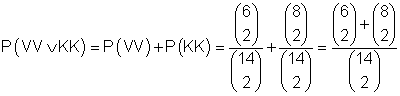
(2) Werden x Vokale dazu getan, dann gilt für die Anzahl der Vokale: 8 + x
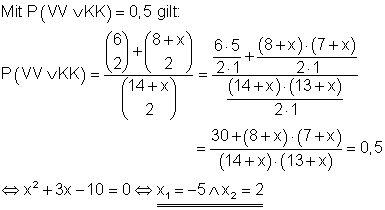
Es müssen 2 Karten mit Konsonanten dazugegeben werden. Das gleiche Ergebnis (P = 0,5) würde man erhalten, wenn man 5 Konsonanten entfernt.
Hier findest du die Aufgaben hierzu.
Und hier die Theorie: Kombinatorik.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

