Lösungen zum Hypothesentest II

Hier findest du die Lösungen der Aufgaben zum Hypothesentest II, dabei sollst du z. B. einen Hypothesentest mit einem bestimmten Signifikanzniveau aufstellen. Danach das Ergebnis kommentieren.

1. Aufgabe

Die Firma „Schlemmerland“ behauptet, dass ihre Konkurrenzfirma „Billigfood“ die Gewichtsangabe, die auf deren Kaviarverpackungen steht häufiger als 5% unterschreitet und damit die Kunden betrügt. Erlaubt ist, dass maximal 5% der Packungen Untergewicht haben. „Billigfood“ dementiert:
„Weniger als 5% der Verpackungen haben Untergewicht“.
Eine unabhängige Kommission untersucht 300 Packungen.

Stelle aufgrund der unterschiedlichen Interessenlagen beider Firmen jeweils einen Hypothesentest mit einem Signifikanzniveau von höchstens 5% auf! Kommentiere die Ergebnisse!

1.  Ausführliche Lösung

Aufgabenanalyse und Aufstellen der Hypothesen

Aus Sicht jeder Firma ist ein Hypothesentest aufzustellen. Aufgrund der unterschiedlichen Interessen unterscheiden sich die aufzustellenden Hypothesen. Damit unterscheiden sich auch jeweils der Annahme- und Ablehnungsbereich.

„Schlemmerland“ möchte zeigen, dass p > 0,05 gilt und stellt folgende Hypothesen auf:
Nullhypothese H₀: p ≤ 0,05; Alternativhypothese H₁: p > 0,05.
Das ist ein rechtsseitiger Hypothesentest.

„Billigfood“ möchte zeigen, dass p < 0,05 gilt und stellt folgende Hypothesen auf:
Nullhypothese H₀: p ≥ 0,05; Alternativhypothese H₁: p < 0,05.
Das ist ein linksseitiger Hypothesentest.

Test für „Schlemmerland“

Nullhypothese H_0 : p \leq 0,05 \quad Signifikanzniveau \quad \alpha \leq 5 \%   \\ Daten: n = 300; \quad  p = 0,05; \\ \mu = n \cdot p = 300 \cdot 0,05 = 15 \\ \sigma = \sqrt {n \cdot p \cdot (1 - p)} = \sqrt {15 \cdot 0,95} = \sqrt {14,25} \approx 3,775 > 3

Bei einem Signifikanzniveau von 5% sind folgende Intervalle zu betrachten:
{ 5% } { 90% } { 5 % } = Ablehnungbereich für H₀.

Damit wird \mu  + 1,64 \cdot  \sigma  \\ = 15 + 1,64 \cdot \sqrt {14,25} \approx  21,19 \quad gerundet \quad auf \quad 21
die obere Grenze des Annahmebereis für H₀.

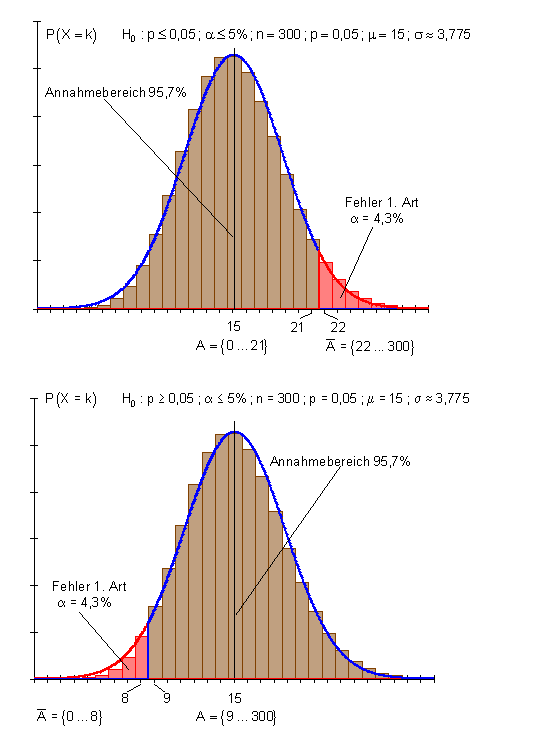
Es gilt: Annahmebereich von H₀ A = {0 … 21}
Ablehnungsbereich von H₀. \bar A =  {22 … 300}

Zu prüfen ist der Ablehnungsbereich derart, dass gilt:
P(22 \leq x \leq 300) \leq \alpha = 5 \%
{0 … 8} {9…15 … 21} {22 … 300}
P(22 \leq x \leq 300) = \frac{1}{2} [1 - P ( \color{blue}{9 \leq x \leq 21})] 
P(9 \leq x \leq 21) \Rightarrow r = 6,5 \Rightarrow \\ z = \frac {r}{\sigma} = \frac{6,5}{\sqrt{14,25}} \approx  1,72 \\ \Rightarrow P(9 \leq x \leq 21) \approx 0,915 \\ \Rightarrow P(22 \leq x \leq 300) \approx \frac{1}{2} [1 - 0,915] = 0,043

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 finden Sie hier.
Dort findest du auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.

Test für „Billigfood“

Nullhypothese H_0 : p \geq 0,05 \quad Signifikanzniveau \quad \alpha \leq 5 \%   \\ Daten: n = 300; \quad  p = 0,05; \\ \mu = n \cdot p = 300 \cdot 0,05 = 15 \\ \sigma = \sqrt {n \cdot p \cdot (1 - p)} = \sqrt {15 \cdot 0,95} = \sqrt {14,25} \approx 3,775 > 3

Bei einem Signifikanzniveau von 5% sind folgende Intervalle zu betrachten:
Ablehnungbereich für H₀ = { 5% } { 90% } { 5 % }.

Damit wird \mu  - 1,64 \cdot  \sigma  \\ = 15 - 1,64 \cdot \sqrt {14,25} \approx  8,81 \quad gerundet \quad auf \quad 9
die untere Grenze des Annahmebereis für H₀.

Es gilt: Annahmebereich von H₀ A = {9 … 300}
Ablehnungsbereich von H₀ \bar A =  {0 … 8}.

Zu prüfen ist der Ablehnungsbereich derart, dass gilt:
P(0 \leq x \leq 8) \leq \alpha = 5 \%
{0 … 8} {9…15 … 21} {22 … 300}
P(0 \leq x \leq 8) = \frac{1}{2} [1 - P ( \color{blue}{9 \leq x \leq 21})] 
P(9 \leq x \leq 21) \Rightarrow r = 6,5 \Rightarrow \\ z = \frac {r}{\sigma} = \frac{6,5}{\sqrt{14,25}} \approx  1,72 \\ \Rightarrow P(9 \leq x \leq 21) \approx 0,915 \\ \Rightarrow P(0 \leq x \leq 8) \approx \frac{1}{2} [1 - 0,915] = 0,043

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

Auswertung:

Eine Gegenüberstellung zeigt:

„Schlemmerland“

Rechtsseitiger Test
Fehler 1. Art: 4,3%
Falls bei der Kontrolle mehr als 21 Packungen Untergewicht haben, wird H₀ abgelehnt.
„Schlemmerland“ geht dann mit einer Irrtumswahrscheinlichkeit von 4,3% davon aus mehr als 5% aller Packungen seien untergewichtig. Der Betrugsverdacht würde sich erhärten. Falls das Kontrollergebnis in den Annahmebereich von H₀ fällt, muss H₀ zwar angenommen werden, ist aber damit nicht bewiesen.“Billigfood“

Linksseitiger Test
Fehler 1. Art: 4,3%
Falls bei der Kontrolle weniger als 9 Packungen Untergewicht haben, wird H₀ abgelehnt.
„Billigfood“ geht dann mit einer Irrtumswahrscheinlichkeit von 4,3% davon aus, weniger als 5% untergewichtige Packungen zu haben. Falls das Kontrollergebnis in den Annahmebereich von H₀ fällt, muss H₀ zwar angenommen werden, ist aber damit nicht bewiesen. Vergleich eines rechtsseitigen mit einem linksseitigen Hypothesentest

Bemerkung zur errechneten Irrtumswahrscheinlichkeit

Die Berechnung der Intervallwahrscheinlichkeiten für die jeweiligen Ablehnungsbereiche erfolgte mit den Tabellenwerten der Normalverteilung. Die Werte der Normalverteilung sind symmetrisch zum Erwartungswert. Gleiche Umgebungsradien bedeuten gleiche Flächen bzw. %- Werte. Die in der Grafik dargestellten Säulen repräsentieren die Binomialverteilung. Diese ist nur bei p = 0,5 symmetrisch zum Erwartungswert. Eine genaue Rechnung mit den Werten der Binomialverteilung würde beim rechtsseitigen Test einen Fehler von 4,9% und beim linksseitigen Test von 3,4% zeigen. Dieser Unterschied liegt an der extremen Schiefheit der Binomialverteilung bei p = 0,05.

2. Aufgabe

Bei der letzten Notenkonferenz einer gymnasialen Oberstufe hatten 15% der Schüler in einigen Fächern Defizite. Im laufenden Schuljahr werden Stützkurse für die kritischen Fächer angeboten. Bei der nächsten Notenkonferenz haben 18 von 140 Schülern Defizite.

a) Kann man mit einer Irrtumswahrscheinlichkeit von höchstens 5% annehmen, dass das Engagement der Lehrkräfte Erfolg hatte?

b) Die Nullhypothese wird aufgrund des Tests abgelehnt.
Wie groß ist der Fehler 1. Art?

2. Ausführliche Lösungen

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

a) Aufgabenanalyse und aufstellen der Hypothesen

Hatte das Engagement der Lehrkräfte Erfolg? Falls ja, dann sollten weniger als 15% aller Schüler Defizite aufweisen. Die Untersuchung soll zeigen, dass p < 0,15 gilt.
Damit werden folgende Hypothesen aufgestellt:
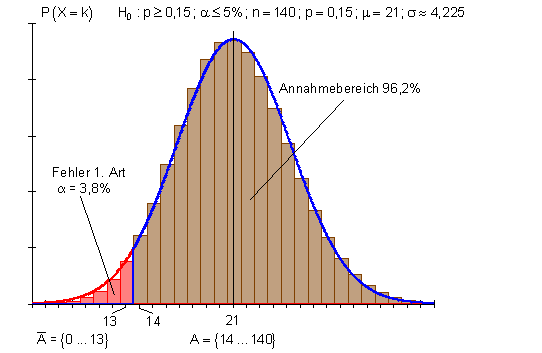
Nullhypothese H₀: p ≥ 0,15; Alternativhypothese H₁: p < 0,15.
Die Nullhypothese ist nur dann abzulehnen, wenn bei wenigen Schülern Defizite auftreten. Man sagt auch kleine Werte von X sprechen gegen H₀. Das ist ein linksseitiger Hypothesentest.

Nullhypothese H_0 : p \geq 0,05 \quad Signifikanzniveau \quad \alpha \leq 5 \%   \\ Daten: n = 140; \quad  p = 0,15; \\ \mu = n \cdot p = 140 \cdot 0,15 = 21 \\ \sigma = \sqrt {n \cdot p \cdot (1 - p)} = \sqrt {21 \cdot 0,85} = \sqrt {17,85} \approx 4,225 > 3

Bei einem Signifikanzniveau von 5% sind folgende Intervalle zu betrachten:
Ablehnungbereich für H₀ = { 5% } { 90% } { 5 % }.

Damit wird \mu  - 1,64 \cdot  \sigma  \\ = 21 - 1,64 \cdot \sqrt {17,85} \approx  14,07 \quad gerundet \quad auf \quad 14
die untere Grenze des Annahmebereis für H₀.

Es gilt: Annahmebereich von H₀ A = {14 … 140}
Ablehnungsbereich von H₀ \bar A =  {0 … 13}.

Zu prüfen ist der Ablehnungsbereich derart, dass gilt:
P(0 \leq x \leq 13) \leq \alpha = 5 \%
{0 … 13} {14…21 … 28} {29 … 140}
P(0 \leq x \leq 13) = \frac{1}{2} [1 - P ( \color{blue}{14 \leq x \leq 28})] 
P(14 \leq x \leq 28) \Rightarrow r = 7,5 \Rightarrow \\ z = \frac {r}{\sigma} = \frac{7,5}{\sqrt{17,85}} \approx  1,78 \\ \Rightarrow P(14 \leq x \leq 28) \approx 0,925 \\ \Rightarrow P(0 \leq x \leq 13) \approx \frac{1}{2} [1 - 0,925] = 0,038

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

Auswertung:

Der Annahmebereich von H₀ beinhaltet 14 bis 140 Schüler mit Defiziten.
Der Ablehnungsbereich von H₀ beinhaltet 0 bis 13 Schüler mit Defiziten.
Da aber 18 Schüler erneut Defizite aufweisen, fällt das in den Annahmebereich von H₀.
Die Nullhypothese muss beibehalten werden, obwohl weniger Schüler, als zu erwarten wäre, Defizite haben. Man kann von keiner positiven Änderung ausgehen. Erst wenn weniger als 14 Schüler Defizite aufweisen, kann man davon ausgehen, dass das Engagement der Lehrer erfolg hatte. Dabei wäre die Irrtumswahrscheinlichkeit etwa 3,8%.

b) Aufgabenanalyse und aufstellen der Hypothesen.

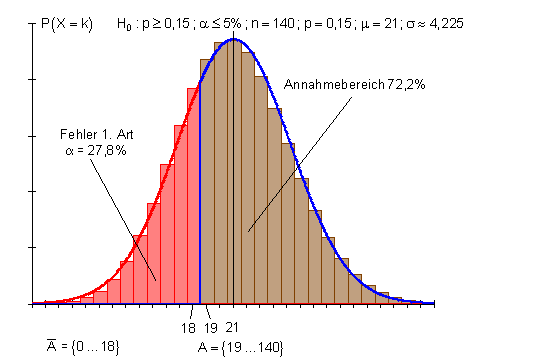
Aufgrund der Tatsache dass 18 Schüler, also weniger als 21, wie bei p = 0,15 zu erwarten wären, Defizite aufweisen, soll die Nullhypothese abgelehnt werden. Dadurch, dass man nun 19 als untere Grenze des Annahmebereichs wählt, ändert sich der Fehler 1. Art. Annahme- und Ablehnungsbereich ändern sich wie folgt.
Annahmebereich: { 19 … 140 } Ablehnungsbereich: { 0 … 18 }
Die Irrtumswahrscheinlichkeit wird durch den Ablehnungsbereich bestimmt.

{0 … 18} {19 … 21 … 23 } {24 … 140}
P(0 \leq x \leq 18) = \frac{1}{2} [1 - P (19 \leq x \leq 23)]  \\ P(19 \leq x \leq 23) \Rightarrow r = 2,5 \Rightarrow \\ z = \frac {r}{\sigma} = \frac{2,5}{\sqrt{17,85}} \approx  0,59 \\ \Rightarrow P(19 \leq x \leq 23) \approx 0,445 \\ \Rightarrow P(0 \leq x \leq 18) \approx \frac{1}{2} [1 - 0,445] = 0,278 = \alpha

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

Auswertung:

Der Annahmebereich von H₀ beinhaltet 19 bis 140 Schüler mit Defiziten.
Der Ablehnungsbereich von H₀ beinhaltet 0 bis 18 Schüler mit Defiziten.

Wird die Nullhypothese schon bei 18 Schülern mit Defiziten abgelehnt, so ist für diese Entscheidung die Irrtumswahrscheinlichkeit etwa 27,8%. Die Aussage, dass das Engagement der Lehrer erfolg hatte, ist also mit einem Fehler von 27,8% behaftet.

3. Aufgabe

Eine Untersuchung ergab, dass Placebos bei vielen Patienten die gleiche Wirkung erzielen wie gleich aussehende echte Tabletten. Die Erfahrung einer Klinik besagt, dass höchstens 60% der Patienten, die Kopfschmerztabletten einnehmen, auf Placebos ansprechen.
Für Berechnungen unter a), b) und c) sind die im Aufgabenblatt beigefügten Tabellen (Tabelle 1 und Tabelle 2) zu verwenden.

a) Ein Klinikarzt behauptet, dass die Wirkung der Placebos verstärkt werden kann, wenn sie einen bitteren Beigeschmack haben. Er verabreicht 100 Patienten die neuen Placebos und stellt fest, dass 75 von ihnen darauf ansprechen.

Muss daraufhin die Nullhypothese H_0 : p_0 \leq 0,6  verworfen werden?
Rechne mit einer Irrtumswahrscheinlichkeit von höchstens 4%!

b) Wie groß ist der Fehler 2. Art, wenn für die bitteren Pillen p = 0,7 gilt?
Wie kann der Fehler 2. Art verringert werden?
Welche Konsequenzen hätte das für den Fehler 1. Art?

c) Reduziere den Fehler 2. Art mindestens auf den halben Wert.
Wie ändern sich dadurch der Annahme- und Ablehnungsbereich von H₀?
Welche Irrtumswahrscheinlichkeit liegt dann vor?

d) Skizziere die Verteilungen aus b) und c) und kennzeichne die Fehler 1. und 2. Art.

3. Ausführliche Lösungen

a) Aufgabenanalyse und Aufstellen der Hypothesen

Benutzen Sie für die Rechnung die beigefügten Tabellen der Binomialverteilung für
n = 100 und p = 0,6, sowie für n = 100 und p = 0,7.

Aufstellen der Hypothesen:
Die Wahrscheinlichkeit dafür, dass Placebos wirken, sei höchstens 60%. Vermutet wird, dass Placebos mit einem bitterem Beigeschmack wirksamer sind. Die Untersuchung soll zeigen, dass p > 0,6 gilt.

Damit werden folgende Hypothesen aufgestellt:
Nullhypothese H₀: p ≤ 0,6; Alternativhypothese H₁: p > 0,6.
Die Nullhypothese ist nur dann abzulehnen, wenn bei vielen Patienten die Placebos wirken. Man sagt auch große Werte von X sprechen gegen H₀. Das ist ein rechtsseitiger Hypothesentest. Der Ablehnungsbereich liegt rechts vom Erwartungswert für p = 0,6 und hat eine Größe von höchstens 4%.

Nullhypothese H_0 : p \leq 0,6 \quad Signifikanzniveau \quad \alpha \leq 4 \%   \\ n = 100; \quad   \mu = n \cdot p_0 = 100 \cdot 0,6 = 60 \\ Es \quad   ist \quad    \sigma = \sqrt {n \cdot p \cdot (1 - p)} = \sqrt {60 \cdot 0,4} = \sqrt {24} \approx 4,899 > 3 \\ 1 - P(X \leq K) \leq 0,04 = \alpha
Aus der Tabelle für n = 100 und p = 0,6 lesen wir für K den Wert 68 ab.
1 - P(X \leq 68) = 1 - 0,98 = 0,04 = \alpha  
Damit ist der Annahmebereich für p \leq 0,6 \\ A = \{0 ... 60 ... 68 \} und der Ablehnungsbereich \bar A = \{69 ... 100 \}

Die Hypothese H₀ wird abgelehnt, da X = 75 im Ablehnungsbereich von H₀ liegt. Die Irrtumswahrscheinlichkeit dieser Entscheidung (Fehler 1. Art) liegt bei etwa 4%.

Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

b)

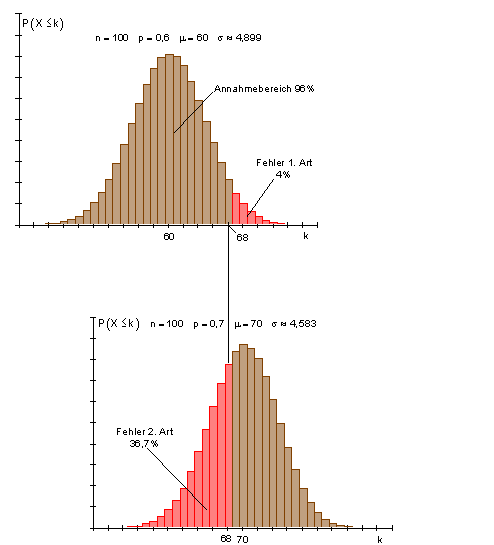
Falls p = 0,7 tatsächlich richtig ist, kann es dennoch vorkommen, dass das Versuchsergebnis in den Annahmebereich von H₀ fällt.
Die Wahrscheinlichkeit, mit der das geschieht, ist der Fehler 2. Art.

Falls für bittere Pillen p = 0,7 gilt, ist der Fehler 2. Art 36,7%.
Die Wahrscheinlichkeit dafür, das die Richtigkeit von p = 0,7 nicht erkannt wird, beträgt etwa 36,7%.
Soll der Fehler 2. Art verringert werden, dann ist der Annahmebereich von H₀ zu verringern. Das hat aber zur Folge, dass dadurch der Fehler 1. Art sich vergrößert.
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

c)

Dadurch, dass der Fehler 2. Art etwa halbiert wird, vergrößert sich der Fehler 1. Art auf etwa das Dreifache.
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50

d) Verteilungen aus Aufgabenteil b)

Ein kleiner Fehler 1. Art führt zu einem großen Fehler 2. Art. Soll der Fehler 2. Art verringert werden, kann das nur durch eine Vergrößerung des Fehlers 1. Art erreicht werden. Verteilungen aus Aufgabenteil c)

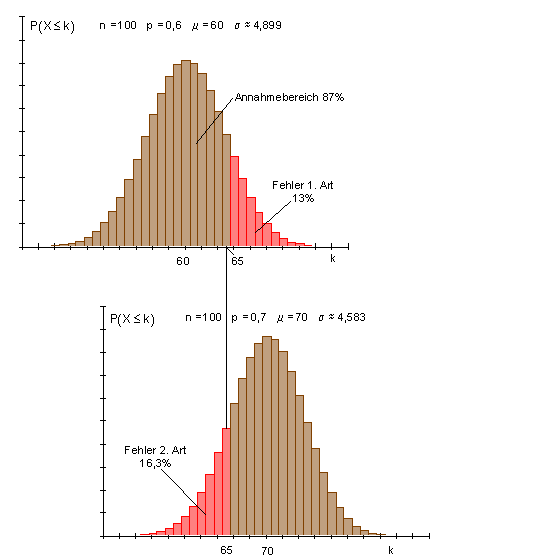
Dadurch, dass der Fehler 2. Art auf etwa die Hälfte reduziert wurde, hat sich der Fehler 1. Art mehr als verdreifacht.

Hier findest du die Aufgaben hierzu.

Und hier die Theorie hierzu Grundlagen zum Hypothesentest.

Und Hypothesentest, ein einfacher Zugang mit Würfeln.

Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.