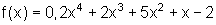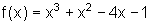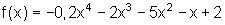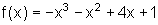In diesem Beitrag erkläre ich die Symmetrie und dem Verlauf ganzrationaler Funktionen.
- Ganzrationale Funktionen n-ten Grades entstehen durch Zusammensetzen von Potenzfunktionen
- Interaktiver Rechner für ganzrationale Funktionen 4. Grades
- Verlauf des Graphen einer ganzrationalen Funktion wird durch den Summanden mit der höchsten Potenz bestimmt
- Symmetrie zu einem beliebigen Punkt
- Interaktiver Rechner für ganzrationale Funktionen bis 9. Grades
- Links zu Trainingsaufgaben und weiteren Beiträge hierzu
Ganzrationale Funktionen n-ten Grades
Eine Funktion f(x) mit f(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + ... + a_2x^2 + a_1x + a_0
heißt ganzrationale Funktion n-ten grades.
Die Zahlen a_n; a_{n-1}; a_{n-2} ... a_2; a_1; a_0 heißen Koeffizienten.
Ganzrationale Funktionen entstehen durch Zusammensetzen von Potenzfunktionen.
Zeichne mit dem Script selber Graphen ganzrationaler Funktionen.
Verlauf des Graphen einer ganzrationalen Funktionen n-ten Grades
Satz:
Der Summanden mit der höchsten Potenz, also xn und an, bestimmen den Verlauf des Graphen einer ganzrationalen Funktion.
Tabelle mit Beispielen:
| n gerade | n ungerade | |
| an>0 | Verlauf von II nach I
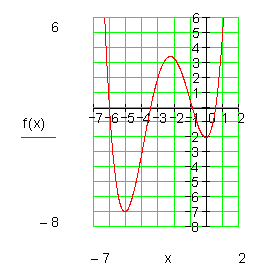
|
Verlauf von III nach I
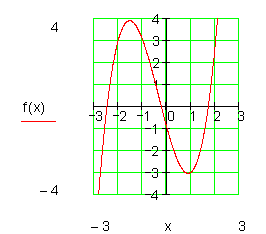
|
| an<0 | Verlauf von III nach IV
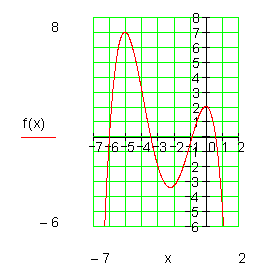
|
Verlauf von II nach IV
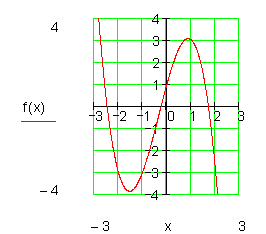
|
Beispiele:
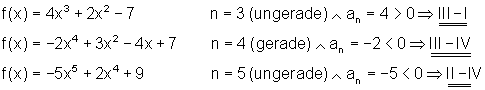
Dazu kannst du dir das 📽️Video Ganzrationale Funktionen Symmetrie und Verlauf ansehen.
Symmetrie des Graphen einer ganzrationalen Funktionen n-ten Grades
Die Vermutung liegt nahe, dass Funktionen, die nur aus Potenzfunktionen mit geraden Exponenten zusammengesetzt sind, achsensymmetrisch sind. Außerdem scheinen Funktionen, die nur aus Potenzen mit ungeraden Exponenten zusammengesetzt sind, punktsymmetrisch zu sein.
Satz:
Der Graph einer ganzrationalen Funktion ist genau dann achsensymmetrisch, wenn deren Funktionsgleichung nur gerade Exponenten enthält.
Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch, wenn deren Funktionsgleichung nur ungerade Exponenten enthält.
Beispiel:
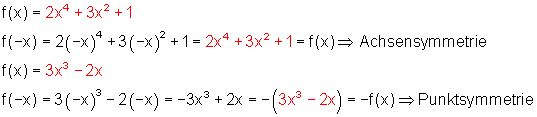
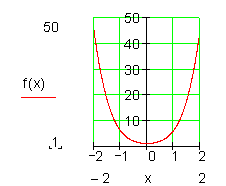

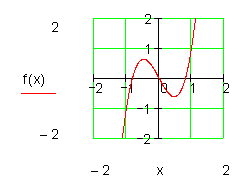

Symmetrie zu einem beliebigen Punkt
Wird der Graph einer punktsymmetrischen Funktion beliebig verschoben, so geht die Symmetrie zum Ursprung, wir nannten sie Punktsymmetrie verloren. In Bezug auf den Zielpunkt der Verschiebung bleibt sie jedoch erhalten.
Beispiel:

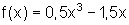
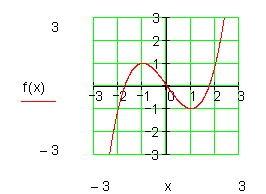
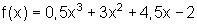
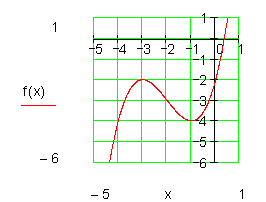
Das Ergebnis leuchtet sofort ein, denn eine Verschiebung des Graphen oder die Verschiebung des Koordinatensystems hat auf die Form des Graphen keinen Einfluss. Lediglich die Funktionsgleichung hat sich geändert.
Fallbeispiel:
Es soll überprüft werden, ob der Graph einer ganzrationalen Funktion 3. Grades zu einem bestimmten Punkt punktsymmetrisch ist. Dazu machen wir ein paar
Vorbetrachtung.
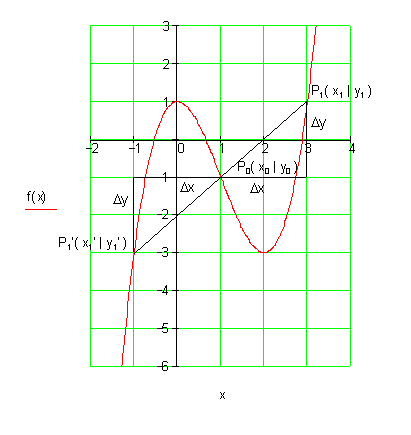

Mit dieser Vorschrift lässt sich stets der bei einer Spiegelung an P0 zu P1 gehörige Spiegelpunkt P1‚ bestimmen.
Beispiel:

Wenn der Spiegelpunkt nicht auf dem Graphen liegt, ist der Graph nicht punktsymmetrisch zu P0.
Rechner für ganzrationale Funktionen bis 9. Grades
Gib die Koeffizienten der Funktionsgleichung ein, danach zeichnet das Javascript den Graph der Funktion.
Dazu findest du hier Trainingsaufgaben.