Hier gibt es Aufgaben zu Formfaktor, Verschiebungen, Scheitelpunkt bei quadratischen Funktionen. Dabei sollst du Wertetabellen aufstellen und Parabeln zeichnen. Im zweiten Teil dann Scheitelpunkte bestimmen. Zuerst stelle ich ausführliche Beispiele als Hilfe zur Verfügung.
Aufgaben 1 bis 10: Wertetabelle und Parabel zeichnen
Zeichne die Graphen folgender Parabeln!
Lege dazu eine Wertetabelle an!
Ausführliches Beispiel als Hilfestellung:
Um den Graphen einer ganzrationalen Funktion zeichnen zu können, ist in den meisten Fällen notwendig, eine Wertetabelle aufzustellen. Dazu ist ein Taschenrechner hilfreich, aber nicht immer notwendig.
Einfaches Beispiel, wobei die Funktionswerte ohne Taschenrechner berechnet werden.
Funktionsgleichung: f(x) = x2 – 4x + 3
Zuerst berechnen wir x = 0.
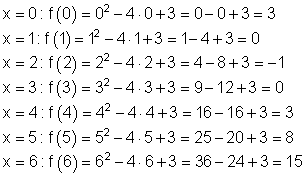
Sobald der Funktionswert größer als |10| wird, kann man in den meisten Fällen aufhören.
Danach berechnen wir die Funktionswerte für negative x – Werte.
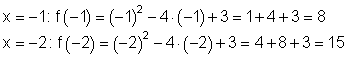
Anschließend tragen wir alle Werte in die Wertetabelle ein.
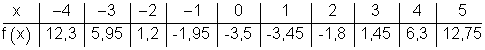
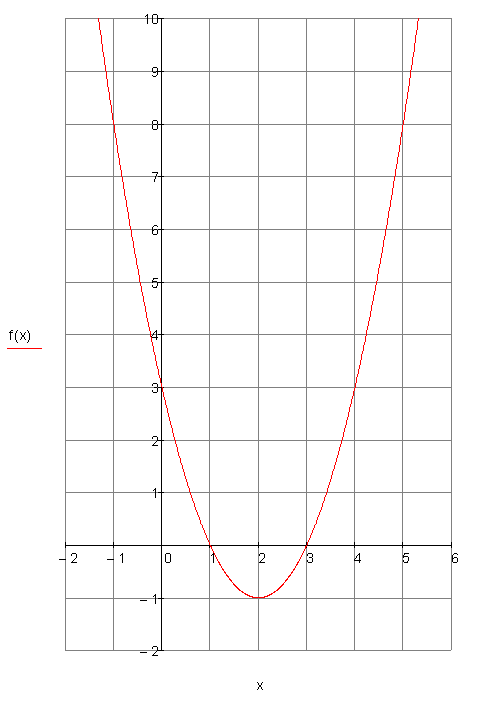
Schließlich können wir mit den so erhaltenen Werten den Graph von f(x) zeichnen. Wenn sich beim zeichnen herausstellt, dass noch Zwischenwerte fehlen, kann man diese nachträglich berechnen.
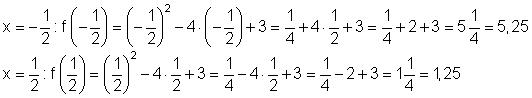
Nicht jeder ist fit mit dem Taschenrechner. Um herauszufinden, wie gut du mit dem Taschenrechner umgehen kannst, berechne die letzten beiden Funktionswerte mit dem Rechner!
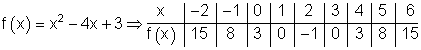
Anspruchsvolles Beispiel, bei dem zur Lösung teilweise der Taschenrechner verwendet wird.
Zuerst berechnen wir x = 0.
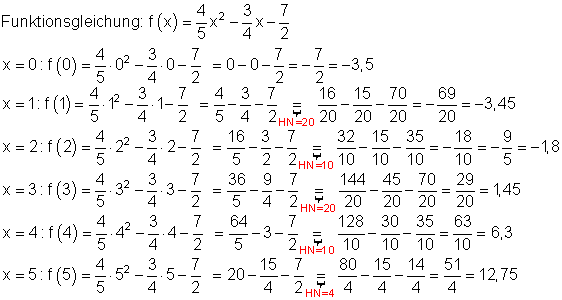
Anschließend werden die Funktionswerte für negative x -Werte berechnet.
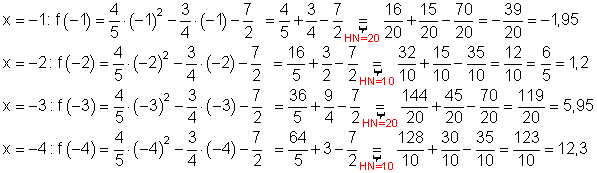
Danach werden alle Werte in die Wertetabelle eingetragen.
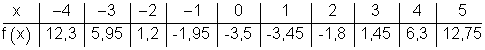
Schließlich zeichnen wir mit den so erhaltenen Werten den Graph von f(x). Falls sich beim zeichnen herausstellt, dass noch Zwischenwerte fehlen, kann man diese nachträglich berechnen.
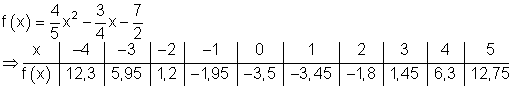
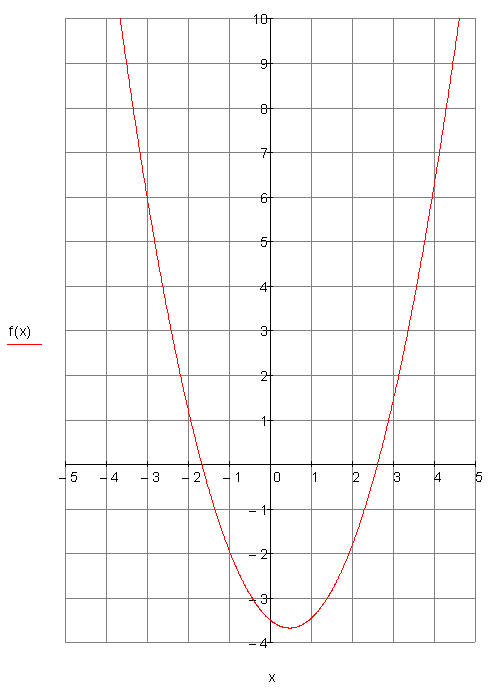
Interaktiv Parabelanalysator: Gib die Koeffizienten ein, dann berechnet und zeichnet das Javascript den Graphen.
Interaktiv: Graphen zeichnen Gib die Koeffizienten und die Potenz für x ein, dann zeichnet das Javascript den Graphen.
Zeichne die Graphen folgender Parabeln!
Lege dazu eine Wertetabelle an!
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Aufgaben 11 bis 21: Scheitelpunkt bestimmen durch quadratische Ergänzung
Gegeben ist die Funktionsgleichung f(x) einer Parabel (ganzrationale Funktion 2. Grades).
Bestimme für folgende Parabeln die Scheitelpunktform und den Scheitelpunkt!
Zeichne den Graphen!
Ausführliches Beispiel als Hilfestellung hierzu:
Aus der allgemeinen Funktionsgleichung der quadratischen Funktion klammern wir den Faktor vor der Variablen x2 aus. Aber nur, wenn er von 1 verschieden ist. Dadurch können wir die quadratische Ergänzung in der so entstandenen Klammer ausführen. Nachdem wir die quadratisch ergänzt haben, multiplizieren wir den zuvor ausgeklammerte Faktor zurück. Beim Ausklammern müssen wir folgendes berücksichtigen: Falls vor der Variablen x2 nur die Zahl 1 oder nichts steht, kann sofort mit der quadratischen Ergänzung begonnen werden. Anderenfalls muss der Formfaktor ausgeklammert werden.
Bestimme für folgende Parabeln die Scheitelpunktform und den Scheitelpunkt!
Zeichne den Graphen!
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Dazu findest du hier die Ausführliche Lösungen.
Und hier eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu weiteren Aufgaben.
