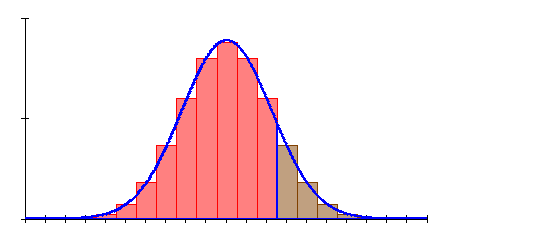
Hier findest du die Lösungen zu Aufgaben Binominalverteilung V, Wieder geht es um Umgebungswahrscheinlichkeiten in Mathe.
1.
n = 20 und p = 0,5.
a) Die Anzahl der Erfolge beträgt höchstens 12
b) Die Anzahl der Erfolge beträgt mindestens 10
c) Die Anzahl der Erfolge beträgt genau 11
d) Die Anzahl der Erfolge liegt zwischen 8 und 12 (einschließlich)
1. Ausführliche Lösungen
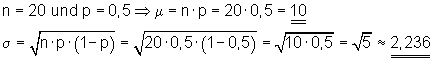
a) Die Anzahl der Erfolge beträgt höchstens 12
![]()
b) Die Anzahl der Erfolge beträgt mindestens 10
![]()
c) Die Anzahl der Erfolge beträgt genau 11
![]()
d) Die Anzahl der Erfolge liegt zwischen 8 und 12 (einschließlich)
![]()
2.

a) Die Anzahl der Erfolge beträgt genau 10
b) Die Anzahl der Erfolge beträgt mindestens 11
c) Die Anzahl der Erfolge liegt zwischen 7 und 13 (einschließlich)
d) Die Anzahl der Erfolge beträgt höchstens 8
2. Ausführliche Lösungen
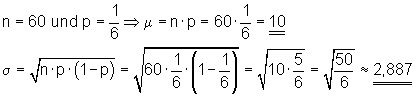
a) Die Anzahl der Erfolge beträgt genau 10
![]()
b) Die Anzahl der Erfolge beträgt mindestens 11
![]()
c) Die Anzahl der Erfolge liegt zwischen 7 und 13 (einschließlich)
![]()
d) Die Anzahl der Erfolge beträgt höchstens 8
![]()
3.
![]()
a) Die Anzahl der Erfolge beträgt genau 10
b) Die Anzahl der Erfolge beträgt mindestens 9
c) Die Anzahl der Erfolge liegt zwischen 6 und 14 (einschließlich)
d) Die Anzahl der Erfolge beträgt höchstens 12
3. Ausführliche Lösungen
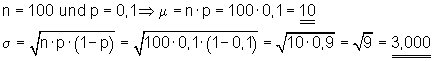
a) Die Anzahl der Erfolge beträgt genau 10
![]()
b) Die Anzahl der Erfolge beträgt mindestens 9
![]()
c) Die Anzahl der Erfolge liegt zwischen 6 und 14 (einschließlich)
![]()
d) Die Anzahl der Erfolge beträgt höchstens 12
![]()
4.
![]()
a) Die Anzahl der Erfolge beträgt mindestens 75
b) Die Anzahl der Erfolge beträgt genau 70
c) Die Anzahl der Erfolge beträgt höchstens 65
d) Die Anzahl der Erfolge liegt zwischen 65 und 75 (einschließlich)
4. Ausführliche Lösungen
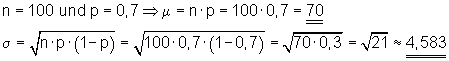
a) Die Anzahl der Erfolge beträgt mindestens 75
![]()
b) Die Anzahl der Erfolge beträgt genau 70
![]()
c) Die Anzahl der Erfolge beträgt höchstens 65
![]()
d) Die Anzahl der Erfolge liegt zwischen 65 und 75 (einschließlich)
![]()
5.
![]()
a) Die Anzahl der Erfolge beträgt genau 48
b) Die Anzahl der Erfolge beträgt höchstens 65
c) Die Anzahl der Erfolge liegt zwischen 42 und 54 (einschließlich)
d) Die Anzahl der Erfolge liegt zwischen 36 und 60 (einschließlich)
e) Die Anzahl der Erfolge liegt zwischen 30 und 66 (einschließlich)
f) Die Anzahl der Erfolge liegt in der einfachen Sigma- Umgebung
g) Die Anzahl der Erfolge liegt in der doppelten Sigma- Umgebung
h) Die Anzahl der Erfolge liegt in der dreifachen Sigma- Umgebung
i) In welcher Sigma- Umgebung liegen 90% aller Erfolge?
j) In welcher Sigma- Umgebung liegen 95% aller Erfolge?
k) In welcher Sigma- Umgebung liegen 99% aller Erfolge?
5. Ausführliche Lösungen
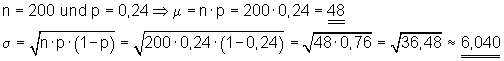
a) Die Anzahl der Erfolge beträgt genau 48
![]()
b) Die Anzahl der Erfolge beträgt höchstens 65
![]()
c) Die Anzahl der Erfolge liegt zwischen 42 und 54 (einschließlich)
![]()
d) Die Anzahl der Erfolge liegt zwischen 36 und 60 (einschließlich)
![]()
e) Die Anzahl der Erfolge liegt zwischen 30 und 66 (einschließlich)
![]()
f) Die Anzahl der Erfolge liegt in der einfachen Sigma- Umgebung
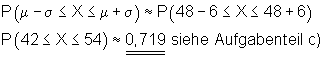
g) Die Anzahl der Erfolge liegt in der doppelten Sigma- Umgebung

h) Die Anzahl der Erfolge liegt in der dreifachen Sigma- Umgebung

i) In welcher Sigma- Umgebung liegen 90% aller Erfolge?
Ansatz mit r = 10.

Der gesuchte Radius liegt zwischen den Werten 9 und 10. Da es sich bei der Binomialverteilung um eine diskrete Verteilung handelt, muss man sich für den Radius entscheiden, der der gewünschten Wahrscheinlichkeit am nächsten liegt. In diesem Fall ist das der Radius r = 9. Teilt man diesen Wert durch Sigma, dann lässt sich der Radius als vielfaches von Sigma darstellen.
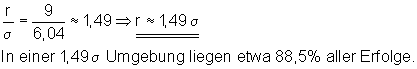
j) In welcher Sigma-Umgebung liegen 95% aller Erfolge?
Ansatz mit r = 12.

Der gesuchte Radius liegt zwischen den Werten 11 und 12. Der Radius r = 11 liegt der gewünschten Wahrscheinlichkeit am nächsten.
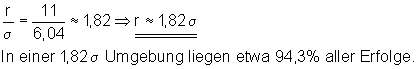
k) In welcher Sigma-Umgebung liegen 99% aller Erfolge?
Ansatz mit r = 14.

Der gesuchte Radius hat den Wert r = 15
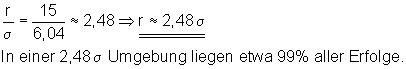
6.
Berechne die Aufgaben 1 bis 4 mit der Tabelle (siehe 123mathe.de/aufgaben-zur-binomialverteilung-v) der Wahrscheinlichkeiten für Sigma-Umgebungen normalverteilter Zufallsvariablen. Und bestimme die prozentuale Abweichung bezogen auf obige Ergebnisse.
6. Ausführliche Lösung 1a)
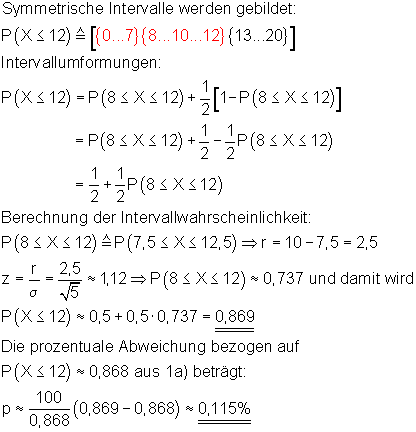
Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.

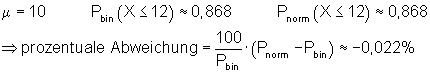
6. Ausführliche Lösung 1b)
![]()
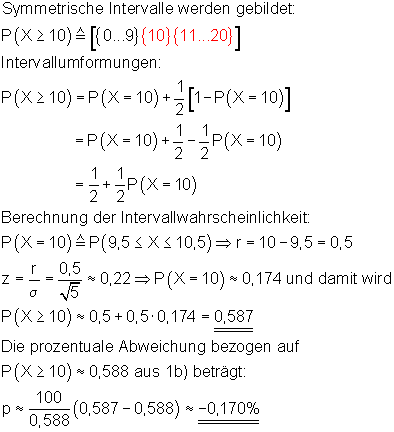
Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
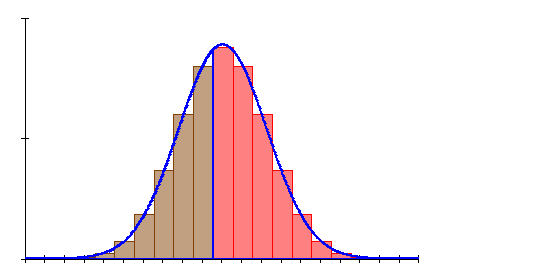
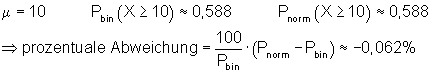
6. Ausführliche Lösung 1c)
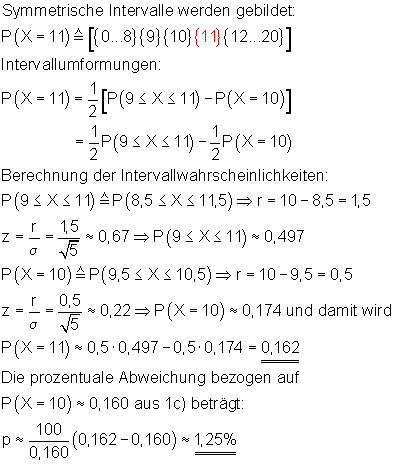
Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
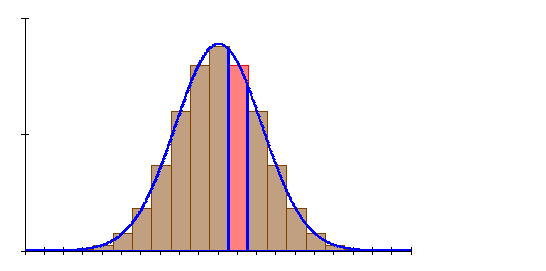
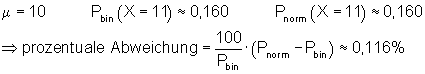
6. Ausführliche Lösung 1d)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
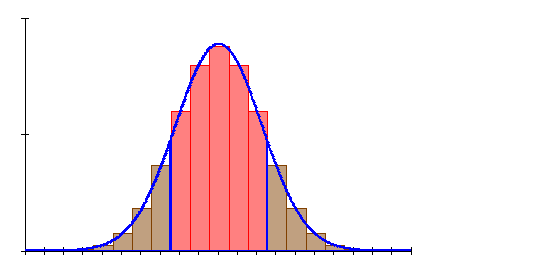
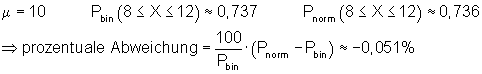
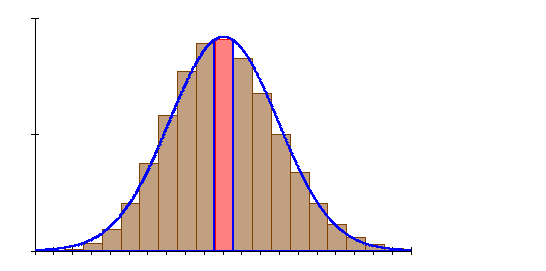
6. Ausführliche Lösung 2a)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
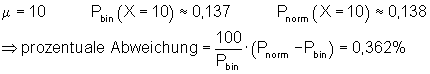
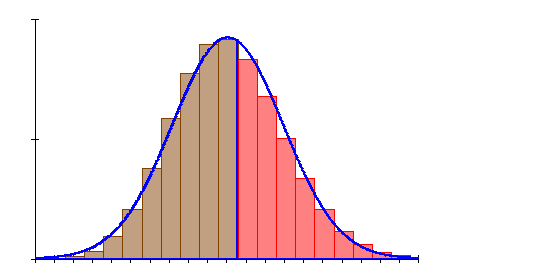
6. Ausführliche Lösung 2b)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
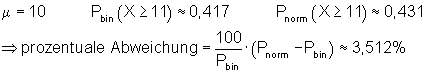
6. Ausführliche Lösung 2c)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
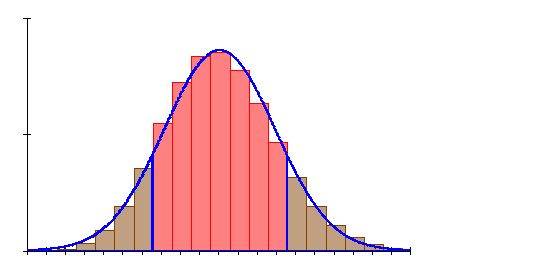
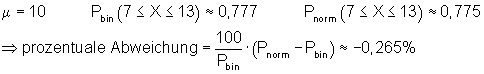
6. Ausführliche Lösung 2d)
![]()
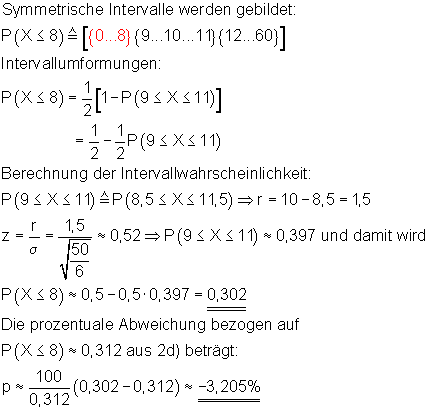
Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
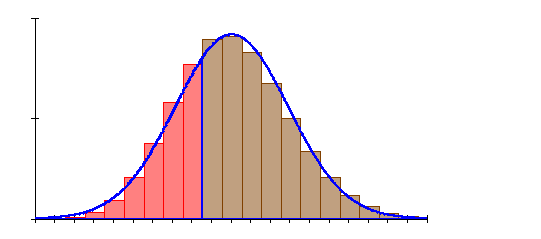
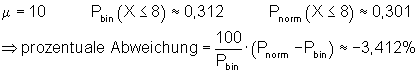
6. Ausführliche Lösung 3a)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
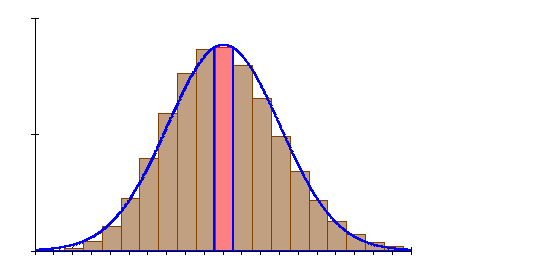
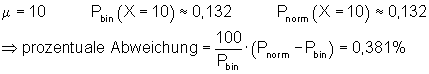
6. Ausführliche Lösung 3b)
![]()
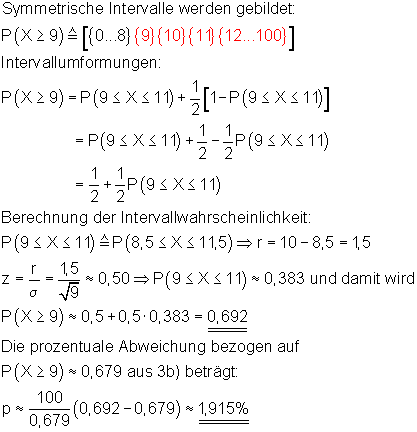
Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
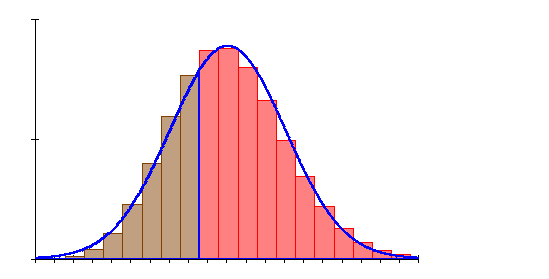
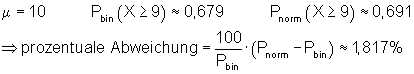
6. Ausführliche Lösung 3c)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
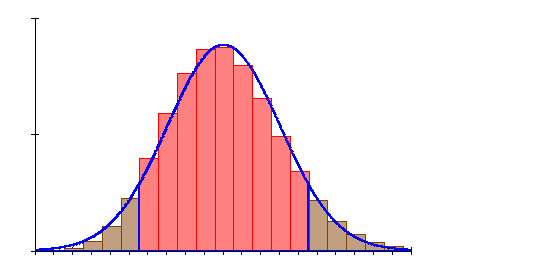
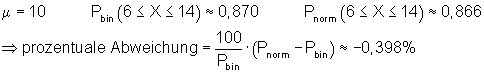
6. Ausführliche Lösung 3d)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
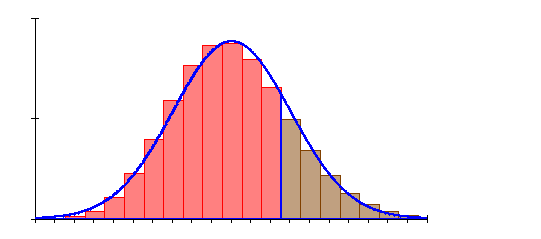
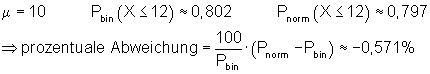
6. Ausführliche Lösung 4a)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
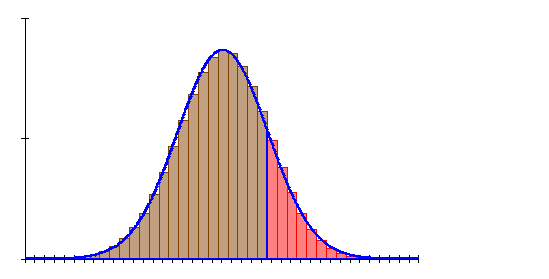
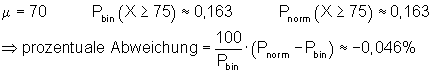
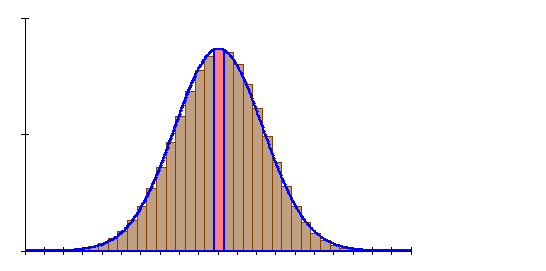
6. Ausführliche Lösung 4b)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
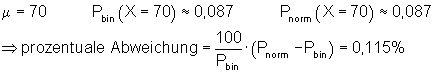
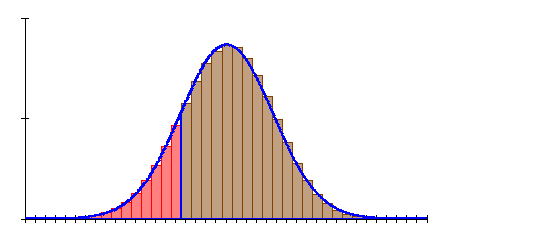
6. Ausführliche Lösung 4c)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
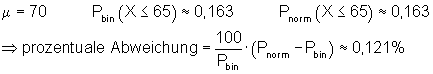
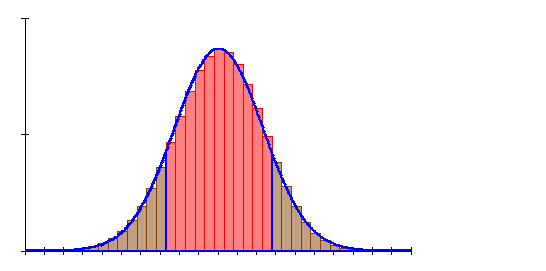
6. Ausführliche Lösung 4d)
![]()

Grafik, Intervallwahrscheinlichkeit und prozentuale Abweichung von der Binomialverteilung wurden mit Mathcad berechnet. Abweichungen zu den oben berechneten Werten beruhen darauf, dass die der Rechnung zugrunde liegenden Tabellenwerte gerundet sind.
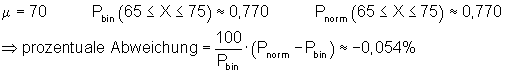
Hier findest du die Aufgaben.
und weitere Aufgaben hierzu: Aufgaben zur Binomialverteilung IV.
Hier finden Sie die Theorie hierzu: Bernoulli-Versuche und die Binomialverteilung.
und Approximation der Binomialverteilung durch die Normalverteilung.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu den Aufgaben I bis IV.

