Hier findest du die vermischten Lösungen der Aufgaben zu linearen Gleichungen.
Dazu können dir diese Videos helfen: Playlist aller Videos zu linearen Gleichungen .
1. a) Löse die Gleichung nach x auf!
Ausführliche Lösung:
20 x - 3(5x + 7) = -2(3 - x)
\Leftrightarrow 20x - 15 x - 21 = -6 + 2x \\
\Leftrightarrow 5x - 21 = -6 + 2x
| -2x \\ \Leftrightarrow 3- - 21 = -6 | + 21 \\
\Leftrightarrow 3x = 15 | : 3 \\
\Leftrightarrow \underline{\underline{x = 5}}
Vorgehensweise:
– auf beiden Seiten der Gleichung die Produkte ausmultiplizieren
– gleiche Summanden zusammenfassen
– Summanden mit x durch Äquivalenzumformungen auf die linke Seite bringen
– beide Seiten der Gleichung durch den Faktor, der vor x steht dividieren so dass x auf der linken Seite übrig bleibt
1. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
5x - (8 + 9x) = 12
\Leftrightarrow 5x - 8 - 9x = 12 \\
\Leftrightarrow -4x - 8 = 12
\quad | + 8 \\ \Leftrightarrow -4x = 20 | : (-4) \\
\Leftrightarrow \underline{\underline{x = -5}}
1. c) Löse die Gleichung nach x auf!
Ausführliche Lösung
(2x - 3) (x - 3) = (x - 1)(2x - 8) + 6
\Leftrightarrow 2x^2 - 6x - 3x + 9 = 2x^2 - 8x - 2x + 8 + 6 \\
\Leftrightarrow \cancel{2x^2} - 9x + 9
= \cancel{2x^2} - 10x + 14 \\ \Leftrightarrow
-9x + 9 = - 10x + 14 | + 10x \\
\Leftrightarrow x + 9 = 14 | - 9 \\ \Leftrightarrow \underline{\underline{x = 5}}
Vorgehensweise:
– auf beiden Seiten der Gleichung die Produkte ausmultiplizieren
– Summanden ordnen und zusammenfassen
– da auf beiden Seiten der Summand 2x2 auftritt, kann dieser gestrichen werden
– durch Äquivalenzumformungen x auf die linke Seite bringen
1. d) Löse die Gleichung nach x auf!
Ausführliche Lösung
6x + 5k = 4x + 9k | - 4x \\
\Leftrightarrow 2x + 5k = 9k | - 5k \\ \Leftrightarrow
2x = 4k | : 2
\Leftrightarrow \underline{\underline{x = 2k}}
Bemerkung: k ist eine Formvariable, auch Platzhalter genannt.
1. e) Löse die Gleichung nach x auf!
Ausführliche Lösung
k^2x = -x + k^2 + 3 | + x \\ \Leftrightarrow
k^2x + x = k^2 + 3 \\ \Leftrightarrow
x(k^2 + 1) = k^2 + 3 | :(k^2 + 1)
\Leftrightarrow \underline{\underline{x = \dfrac{k^2 + 3}{k^2 + 1}}}
Vorgehensweise:
– Alle Summanden, die die Variable x enthalten werden auf die linke Seite gebracht
– x wird ausgeklammert
– beide Seiten werden durch den Klammerausdruck dividiert
1. f) Löse die Gleichung nach x auf!
Ausführliche Lösung
\frac{x}{18} - \frac{5}{2} = \frac{3x + 5}{8} - 6 | Hauptnenner = 72 \\ \Leftrightarrow \frac{4 \cdot x}{4 \cdot 18} - \frac{36 \cdot 5}{36 \cdot 2} = \frac{9 \cdot (3x + 5)}{9 \cdot 8} - \frac{72 \cdot 6}{72} | \cdot 72
\Leftrightarrow \frac{4x}{72} - \frac{180}{72} = \frac{9 \cdot (3x + 5)}{72} - \frac{432}{72} | \cdot 72 \\
\Leftrightarrow 4x -180 = 9(3x + 5) - 432 \\ \Leftrightarrow
4x - 180 = 27x + 45 - 432 | - 27x \\ \Leftrightarrow
-23x - 180 = -387 | + 180 \\ \Leftrightarrow
-23x = - 207 | :(-23) \\ \Leftrightarrow \underline{\underline{x = 9}}
Vorgehensweise:
– es handelt sich um eine Bruchgleichung, deren Nenner nur aus Zahlen besteht
– zuerst wird der Hauptnenner bestimmt, das ist das kleinste gemeinsame Vielfache der Nenner (kgV)
![]()
– Multiplikation beider Gleichungsseiten mit dem Hauptnenner lässt eine Gleichung ohne Brüche entstehen
2. Löse die Gleichung nach x auf.!
a)
Ausführliche Lösung
\frac{2x}{3} - 5 = -\frac{5x}{6} - 2 | Hauptnenner = 6
\Leftrightarrow \frac{2 \cdot 2x}{6} - \frac{6 \cdot 5}{6} = -\frac{5x}{6} - \frac{6 \cdot 2}{6} | \cdot 6 \\ \Leftrightarrow
4x - 30 = -5x - 12 | +5x \\ \Leftrightarrow
9x - 30 = -12 | + 30 \\ \Leftrightarrow
9x = 18 | : 9 \\ \Leftrightarrow \underline{\underline{x = 2}}
2. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
\frac{x}{3} - 5 = \frac{x}{5} - 3 | Hauptnenner = 15
\Leftrightarrow \frac{5x}{15} - \frac{15 \cdot 5}{15} = \frac{3x}{15} - \frac{15 \cdot 3}{15} | \cdot 15 \\ \Leftrightarrow
5x - 75 = 3x -45 | -3x \\ \Leftrightarrow
2x -75 = -45 | +75 \\ \Leftrightarrow 2x = 30 | :2 \\ \Leftrightarrow \underline{\underline{x = 15}}
2. c.) Löse die Gleichung nach x auf!
Ausführliche Lösung
4- \frac{x - 5}{4} = \frac{x + 1}{2} - \frac{x - 3}{3} | Hauptnenner = 12
\Leftrightarrow \frac{12 \cdot 4}{12} - \frac{3(x - 5)}{12} = \frac{6 (x + 1)}{12} - \frac{4 (x - 3)}{12} | \cdot 12 \\ \Leftrightarrow
48 - 3(x - 5) = 6 (x + 1) - 4 (x - 3) \\ \Leftrightarrow
48 - 3x + 15 = 6x + 6 - 4x + 12 \\\Leftrightarrow
-3x + 63 = 2x + 18 | - 2x \\ \Leftrightarrow
-5x + 63 = 18 | - 63 \\ \Leftrightarrow
-5x = - 45 | : (-5) \\ \Leftrightarrow \underline{\underline{x = 9}}
Bemerkung:
Um die Brüche auf den Hauptnenner zu bringen, muss Zähler und Nenner mit einer passenden Zahl multipliziert werden.
Dabei ist zu beachten, dass der Zähler in Klammern zu setzen ist, wenn er aus einer Summe besteht.
2. d) Löse die Gleichung nach x auf! Ausführliche Lösung
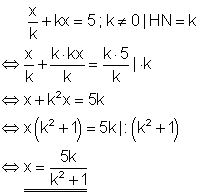
Bemerkung:
Die Formvariable k darf nicht den Wert Null besitzen, denn durch Null darf man nicht teilen.
Nachdem die Bruchgleichung auf den Hauptnenner k gebracht wurde, kann man auf der linken Seite x ausklammern und die rechte Seite durch den Klammerausdruck teilen.
3. Bestimme die Anzahl der Lösungen in Abhängigkeit von k!
a)
Ausführliche Lösung
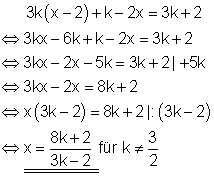
Bemerkung:
Der Lösungsterm ist ein Bruch in dem die Formvariable k vorkommt.
Da der Nenner eines Bruches nicht Null werden darf, kann k nur Werte annehmen für die der Nenner ungleich Null ist.
Man bestimmt also den Wert für k , bei dem der Nenner Null wird und schließt diesen aus.
![]()
Die Lösung gilt also für alle Werte von k außer k = 2/3.
3. b) Bestimme die Anzahl der Lösungen in Abhängigkeit von k! Ausführliche Lösung
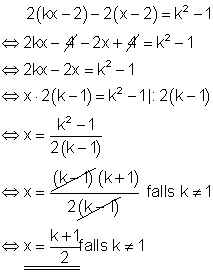
Bemerkung:
Im vorletzten Schritt darf der Bruch nur dann durch ( k – 1 ) gekürzt werden, wenn k ungleich 1 ist, denn sonst würde in dem Bruch 0/0 vorkommen, was nicht definiert ist.
Jetzt ist zu untersuchen, wie die Gleichung aussieht, wenn k = 1 ist.
Dazu wird der Wert 1 für k in die Ausgangsgleichung eingesetzt.
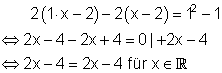
Diese Gleichung gilt für alle x- Werte.
Das bedeutet:
Für k = 1 hat die Gleichung unendlich viele Lösungen und für k ungleich 1 genau eine Lösung.
3. c)
Bestimme die Anzahl der Lösungen in Abhängigkeit von k!
Ausführliche Lösung
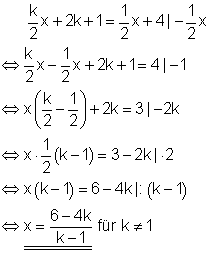
Bemerkung:
Für k = 1 gibt es keine Lösung, da der Nenner des Bruches ungleich Null sein muss.
3. d) Bestimme die Anzahl der Lösungen in Abhängigkeit von k! Ausführliche Lösung
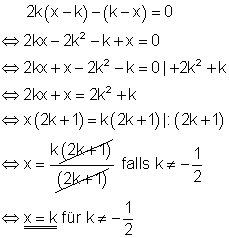
Bemerkung:
Im vorletzten Schritt darf der Bruch nur dann durch ( 2k +1 ) gekürzt werden, wenn k ungleich -1/2 ist, denn sonst würde in dem Bruch 0/0 vorkommen, was nicht definiert ist.
Jetzt ist zu untersuchen, wie die Gleichung aussieht, wenn k = -1/2 ist.
Dazu wird der Wert -1/2 für k in die Ausgangsgleichung eingesetzt.
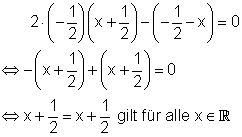
Diese Gleichung gilt für alle x- Werte.
Das bedeutet:
Für k = -1/2 hat die Gleichung unendlich viele Lösungen und für k ungleich -1/2 genau eine Lösung.
3. e) Bestimme die Anzahl der Lösungen in Abhängigkeit von k! Ausführliche Lösung
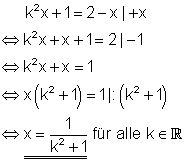
Bemerkung:
Da k2 +1 nie Null werden kann, ist die Division durch k2 +1 für alle k erlaubt.
3. f) Bestimme die Anzahl der Lösungen in Abhängigkeit von k! Ausführliche Lösung
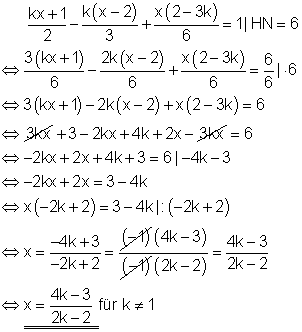
Bemerkung:
Für k = 1 keine Lösung, da der Nenner dann Null würde.
Eine Vorzeichenumkehr im Zähler und im Nenner erreicht man dadurch, dass man den Faktor ( -1 ) ausklammert und kürzt.
4.
a)
Für welche Wahl von a besitzt die Gleichung genau eine, keine oder mehr als eine Lösung?
Ausführliche Lösung
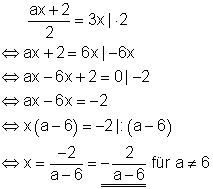
Bemerkung:
Für a = 6 besitzt die Gleichung keine Lösung.
Für alle anderen Werte von a jeweils genau eine Lösung.
4. b) Für welche Wahl von a besitzt die Gleichung genau eine, keine oder mehr als eine Lösung? Ausführliche Lösung
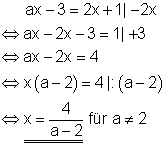
Bemerkung:
Für a = 2 besitzt die Gleichung keine Lösung.
Für alle anderen Werte von a jeweils genau eine Lösung.
4. c)
Für welche Wahl von a besitzt die Gleichung genau eine, keine oder mehr als eine Lösung?
Ausführliche Lösung
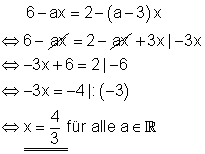
Bemerkung:
Da im Lösungsterm die Formvariable a nicht mehr auftritt, gilt die Lösung für alle Werte von a.
Die Gleichung hat für jeden Wert von a die Lösung 4/3.
4. d) Für welche Wahl von a besitzt die Gleichung genau eine, keine oder mehr als eine Lösung? Ausführliche Lösung
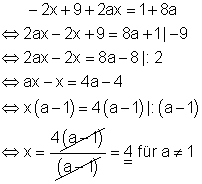
Bemerkung: Falls a = 1 ist gilt:
![]()
Da in diesem Fall für x jede beliebige Zahl die Gleichung erfüllt, hat die Gleichung unendlich viele Lösungen falls a = 1 ist.
Sonst hat sie für jedes a nur die Lösung x = 4.
5.
Ausführliche Lösung
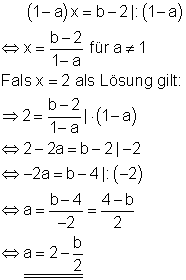
6.
Konstruiere aus der Gleichung andere verschiedenartige Gleichungen, die dieselbe Lösung haben! Ausführliche Lösung
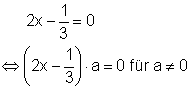
Bemerkung:
Da jede Gleichungsseite wegen der Äquivalenz mit dem gleichen Faktor multipliziert werden darf, kann die Gleichung mit dem Formfaktor a (ungleich Null) multipliziert werden.
Das Ergebnis wird davon nicht beeinflusst.
7.
Die Summe von 5 aufeinander folgenden natürlichen Zahlen ergibt 460. Berechne die größte Zahl!
Ausführliche Lösung
Ansatz:
Die natürliche Zahl sei x.
Die auf x folgende Zahl ist dann (x + 1) und die darauf folgende ( x + 1 ) +1 = ( x + 2) usw.
Damit lässt sich die Summe von 5 aufeinander folgenden Zahlen wie folgt darstellen:
x + (x + 1) + (x + 2) + (x + 3) + (x + 4).
Der Wert der Summe sei 460 und die größte Zahl ist (x + 4).
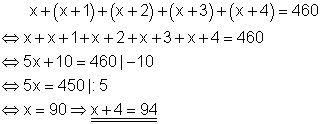
Die größte Zahl lautet 94.
8.
Die Differenz der Quadrate von zwei aufeinander folgenden natürlichen Zahlen ist 55.
Bestimme die beiden Zahlen! Ausführliche Lösung
Ansatz:
Die Zahl sei n.
Zwei aufeinanderfolgende Zahlen sind dann n und n+1.
Die Quadrate dieser sind n2 und (n+1)2 .
Da die Differenz der zwei aufeinander folgenden Zahlen 55 sein soll, muss vom größeren Quadrat das kleinere abgezogen werden.
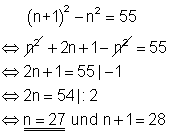
9.
Eine Mauer lässt sich aus 54 Reihen Ziegelsteinen der Höhe x herstellen. Nimmt der Maurer um 1,6 cm höhere Steine, so braucht er nur 45 Reihen. Berechne die Höhe x! Ausführliche Lösung
Ansatz:
Der Ziegelstein hat die Höhe x.
Mit 54 Reihen hat die Mauer eine Höhe von 54x.
Ist der Stein um 1,6 cm höher, so ist die Steinhöhe x+1,6.
Da die gesamte Höhe der Mauer gleich bleiben soll und der Maurer dafür 45 Reihen benötigt, gilt:
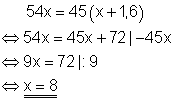
Der ursprüngliche Stein hat eine Höhe von 8 cm.
Hier findest du die Aufgaben.
Und hier die Theorie Lineare Gleichungen zu Sachaufgaben.
Und hier eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

