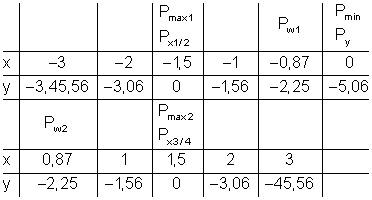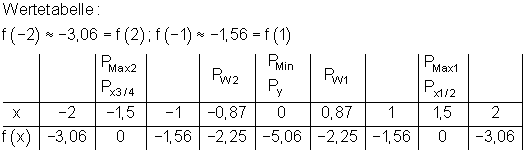Hier findest du ein weiteres Beispiel für die Lösung einer Kurvendiskussion einer ganzrationalen Funktion 4. Grades, auch mit den grafikfähigen Taschenrechnern Casio fx-CG20 und Casio fx-CG50,
Lösung mit dem Casio fx-CG20 und Casio fx-CG50 weiter unten.
1. Definitionsbereich:
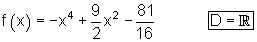
2. Symmetrien:
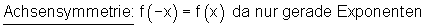
3. Extrema:
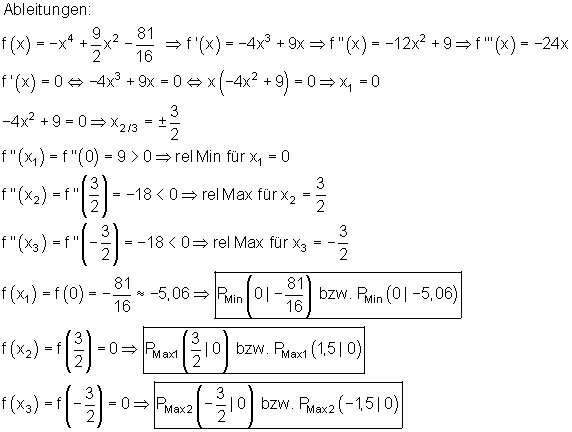
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 unten.
4. Wendepunkte:
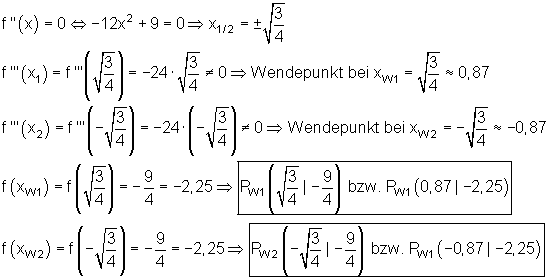
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 unten
5. Achsenschnittpunkte:
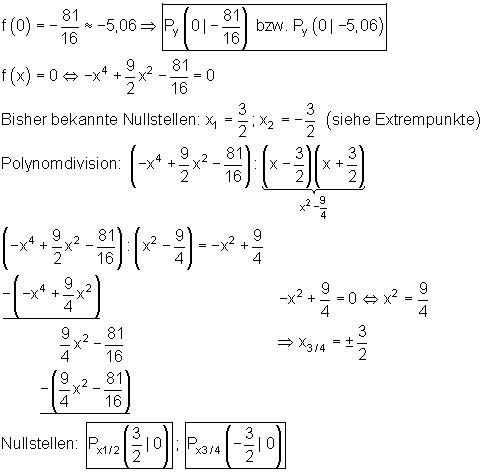
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 unten
6. Wertetabelle und Graph:
Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50 unten.
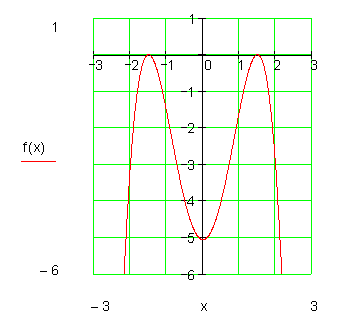
7. Krümmungsverhalten und Monotonie:

8. Randpunkte des Definitionsbereiches:
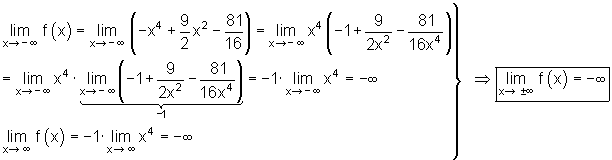
Interaktiv: Kurvendiskussion: Gib einen ganzrationalen Term ein, das Javascript erstellt dann die Kurvendiskussion.
Interaktiv: Nullstellenfinder: Gib einen Term ein, das Javascript berechnet die Nullstellen von Polynomen bis 9. Grades und zeichnet den Funktionsgraphen.
Hier findest du die Theorie: Kurvendiskussion mit Beispielen.
Und hier Aufgaben Differenzialrechnung XI.
Berechnungen mit dem GTR Casio fx-CG20 und Casio fx-CG50
Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 findest du hier.
Dort findest du auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.
Berechne die Extrempunkte von
![]()
Funktionsgleichung mit dem Grafikeditor eingeben und anzeigen:
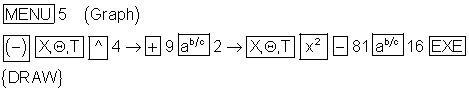
Um den Graphen optimal anzuzeigen, wird das Betrachtungsfenster auf
x: [ -3 ; 3 ] und y: [ -6 ; 1 ] eingestellt.
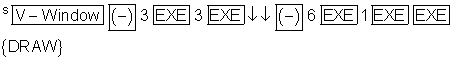
Extremwerte:
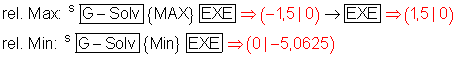
Pmax1 ( -1,5 | 0 ) , Pmax2 ( 1,5 | 0 ) , Pmin ( 0 | -5,0625 )
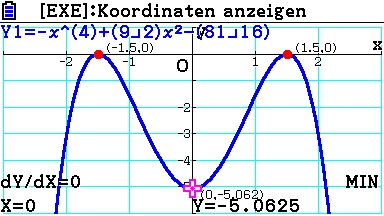
Mit [EXIT] gelangt man zurück in den Grafikeditor.
Extremwertberechnung von
![]()
im Run Matrix Menü
Die Nullstellen der 1. Ableitung von f(x) werden mit SolveN berechnet und angezeigt.
Setzt man einen der angezeigten Werte in f(x) ein, so erhält man den dazugehörigen Extremwert, falls dieser existiert.
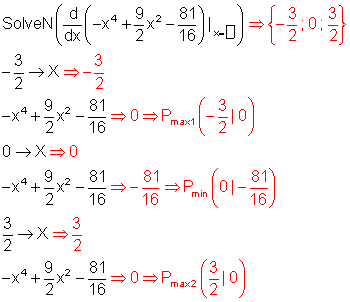
Berechne die Wendepunkte von
![]()
Im Grafikeditor trägt man unterhalb von Y1 f‘ und f“ wie folgt ein:
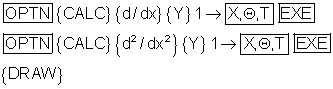
Um die Graphen optimal anzuzeigen, wird das Betrachtungsfenster auf
x: [ -3 ; 3 ] und y: [ -6 ; 8 ] eingestellt.
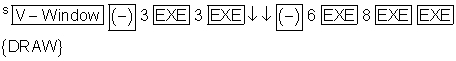
Die Wendestellen befinden sich dort, wo die zweite Ableitung Null ist.

Die Wendestellen liegen bei xw1 = -0,866.. und bei xw2 = 0,866..
Der zugehörige Wendepunkt hat die Koordinaten:
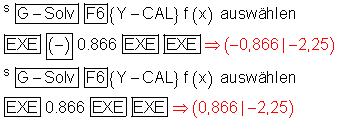
Pw1 ( -0,866 | -2,25 ) und Pw2 ( 0,866 | -2,25)
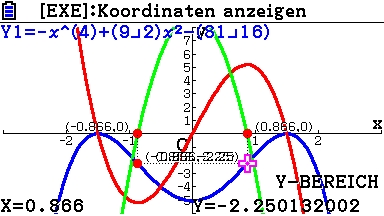
Wendepunktkoordinaten von
![]()
in Bruchdarstellung mit SolveN
Die Nullstellen von f“(x) = -12x2 + 9 liefern die Wendestellen.
Die Nullstellen von f“(x) also xw1 und xw2 werden mit SolveN berechnet und in Liste 3 abgespeichert.
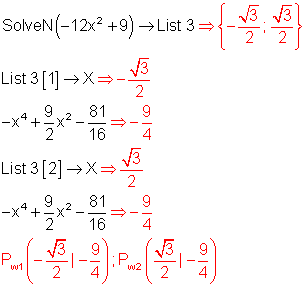
Berechne die Achsenschnittpunkte von
![]()
Die Grafik der Funktion ist im Betrachtungsfenster aufgerufen.
Mit S[Sketch] {Cls} kann der Graph neu gezeichnet werden.
Um den Graphen optimal anzuzeigen, wird das Betrachtungsfenster auf
x: [ -3 ; 3 ] und y: [ -6 ; 1 ] eingestellt.
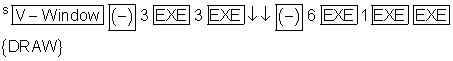
Schnittpunkt mit der y-Achse:
![]()
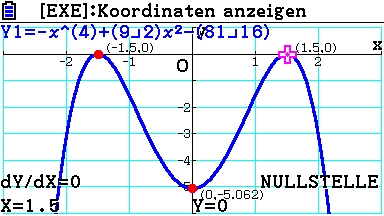
Nullstellen oder Schnittpunkte mit der x-Achse:
![]()
Py ( 0 | -5,0625 ) und Px1/2 ( -1,5 | 0) doppelte Nullstelle Px3/4 ( 1,5 | 0) doppelte Nullstelle
Wertetabelle erstellen für
![]()
Für das Intervall [ -3 ; 3 ] soll eine Wertetabelle mit der Schrittweite 1 erstellt werden.
Wertetabelle (gerundet auf 2 Stellen):