Hier findest du die Lösungen der Mathematik Aufgaben zu ganzrationalen Funktionen aus gegebenen Bedingungen IV mit komplettem Lösungsweg.
1. Ausführliche Lösung
Tipps zur Vorgehensweise:
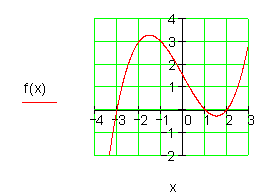
Eine ganzrationale Funktion 3. Grades kann maximal 3 Nullstellen haben. Zwischen der Nullstelle Px1 und dem Punkt P muss ein Hochpunkt liegen. Zwischen den Nullstellen Px2 und Px3 muss ein Tiefpunkt liegen.
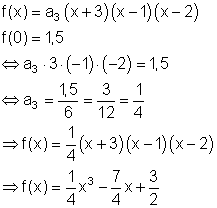
2. Ausführliche Lösung
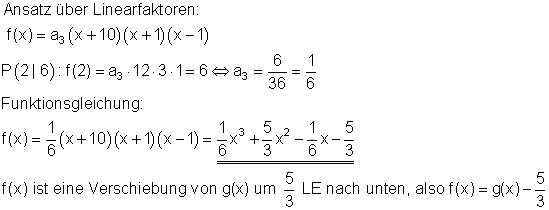
Die Funktionsgleichung:
Wegen der Punktsymmetrie kann folgender Ansatz gemacht werden:

Die Achsenschnittpunkte:
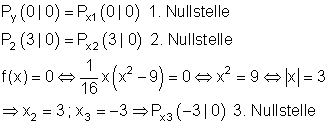
Die Werte für die Wertetabelle werden von Hand berechnet:
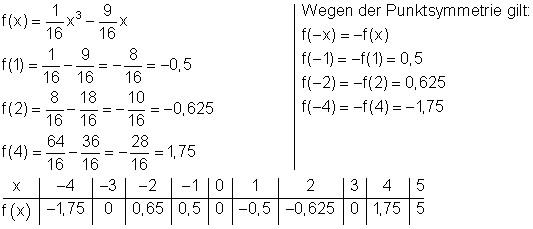

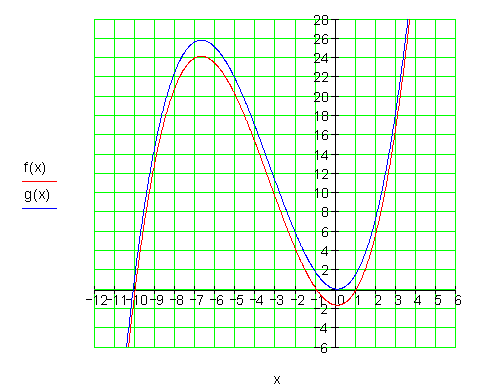
3. Ausführliche Lösung
4. Ausführliche Lösung
a) x muss positiv sein => x > 0
2x muss kleiner als die Seitenlänge sein => 2x < 30 <=> x < 15
| => 0 < x < 15
b)
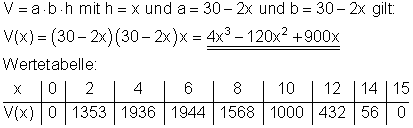
c) Das maximale Volumen der Schachtel liegt bei etwa 2000 cm3 und gilt für einen x- Abschnitt von etwa 5 cm. Eine exakte Berechnung ist erst mit Hilfe der Differentialrechnung möglich.
5. Ausführliche Lösung
a) Ansatz:
Ganzrationale Funktion 3. Grades durch 4 Punkte.
Der Beginn der Zählung 2002 wird als Nullpunkt definiert.
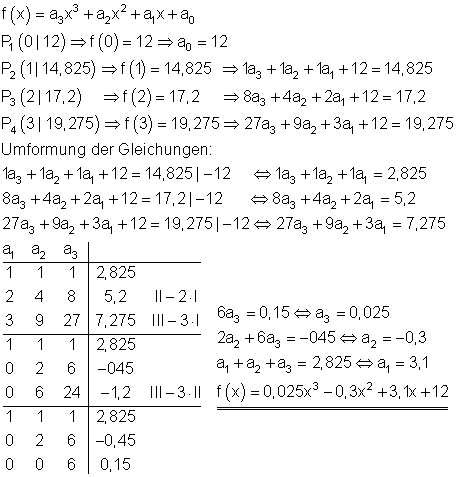
b) Prognosen in GW:
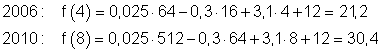
c)Für 2006 übersteigt die Prognose mit 21,2 GW die tatsächlich installierte Leistung von 20,9 GW geringfügig.
Für 2010 übersteigt die Prognose mit 30,4 GW die bis dahin möglicherweise installierte Leistung von 30 GW ebenfalls nur geringfügig.
Hier findest du die Aufgaben.
Die Aufgaben Ganzrationale Funktionen aus gegebenen Bedingungen II und III sind in den Materialien enthalten, die man hier erwerben kann.
Die Theorie findest du hier: Aufstellen der Funktionsgleichung aus gegebenen Bedingungen.
Hier eine Übersicht über alle Beiträge zur weiteren ganzrationalen Funktionen.

