Bei diesen Mathematik Aufgaben zu ganzrationalen Funktionen aus gegebenen Bedingungen IV sollst du Graphen zeichnen etc.
1. Skizziere den Graphen und bestimme den Funktionsterm.
Von einer ganzrationalen Funktion 3. Grades sind die drei Nullstellen und ein weiterer Punkt bekannt.
![]()
2. Bestimme die Funktionsgleichung und die Achsenschnittpunkte.
Eine ganzrationale Funktion 3. Grades ist symmetrisch zum Ursprung und verläuft durch die Punkte P1( 3 | 0 ) und P2( 5 | 5 ).
Stelle eine Wertetabelle auf und zeichne den Graphen.
3. Nullstellen
Eine ganzrationale Funktion 3. Grades f(x) hat die Nullstellen Px1, Px2 und Px3. Der Graph der Funktion f(x) verläuft durch den Punkt P. Bestimme f(x). Wie hängt der Graph von f(x) mit dem von g(x) zusammen?
Daten:
![]()
4. Karton
Aus einem quadratischen Karton der Seitenlänge 30 cm wird durch falten eine Schachtel ohne Deckel mit der Höhe x geformt.
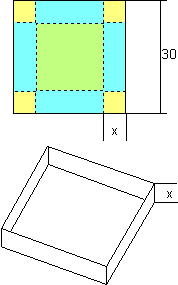
a) Zeige, dass man nur für
0 < x < 15
eine solche Schachtel formen kann.
b) Bestimme einen Funktionsterm, der das Volumen V in Abhängigkeit von x beschreibt.
c) Zeichne den Graphen und bestimme näherungsweise das maximale Volumen.
5. Windkraft
Die als Windkraft installierte elektrische Leistung in Deutschland lässt sich nebenstehender Tabelle entnehmen.
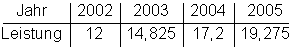
Leistungsangabe in Gigawatt (GW).
a) Ermittele eine Funktion, die die Entwicklung beschreibt.
b) Erstelle eine Prognose für die Jahre 2006 und 2010.
c) Vergleiche die Funktionswerte mit einer installierten Leistung von 20,9 GW in 2006 und dem Ziel von 30 GW in 2010.
Dazu findest du hier die Lösungen.
Und hier die Aufgaben Ganzrationale Funktionen aus gegebenen Bedingungen I.
Die Aufgaben Ganzrationale Funktionen aus gegebenen Bedingungen II und III sind in den Materialien enthalten, die man hier erwerben kann.
Die Theorie findest du hier: Aufstellen der Funktionsgleichung aus gegebenen Bedingungen.
Hier eine Übersicht über alle Beiträge zur weiteren ganzrationalen Funktionen, darin auch Links zu weiteren Aufgaben.

