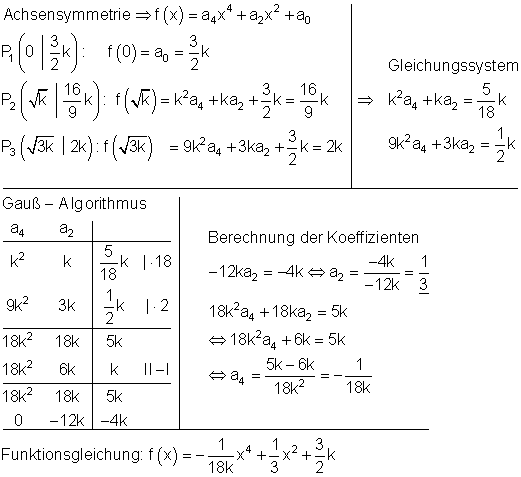Hier findest du die Lösungen der Mathematik Aufgaben zu ganzrationalen Funktionen aus gegebenen Bedingungen I mit komplettem Lösungsweg.
1. Gegeben ist die Wertetabelle einer ganzrationalen Funktion 3. Grades
Es existieren 3 Nullstellen (Wertetabelle).
Der Graph verläuft von II – III – I – IV.
Schnittpunkt mit der y- Achse:
Py( 0 | 1 ).
Punktsymmetrisch zu P( 0 | 1 ).
Bemerkung zur Punktsymmetrie:
Zwei Punkte, P0( x0 | y0 ) und P1( x1 | y1 ) liegen auf dem Graphen von f(x).
Liegt der Spiegelpunkt P1‚( x1‚ | y1‚) ebenfalls auf dem Graphen, so ist der Graph von f(x) symmetrisch zu P0( x0 | y0 ).
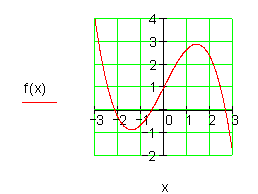
2. Eine ganzrationale Funktion 3. Ordnung verläuft durch die gegebenen Punkt
a) Ausführliche Lösung


Um den Funktionsgraphen zeichnen zu können, benötigen wir zu den in der Aufgabenstellung vorgegebenen Punkten einige zusätzliche. Diese bestimmen wir mit dem Hornerschema.
Dazu kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
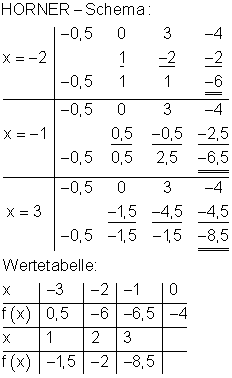
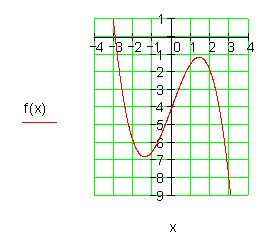
Schnittpunkt mit der y- Achse:
P1( 0 | -4 )
Es existiert nur eine Nullstelle, sie liegt in der Nähe von x = -3.
2. b) Ausführliche Lösung
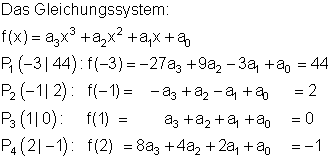
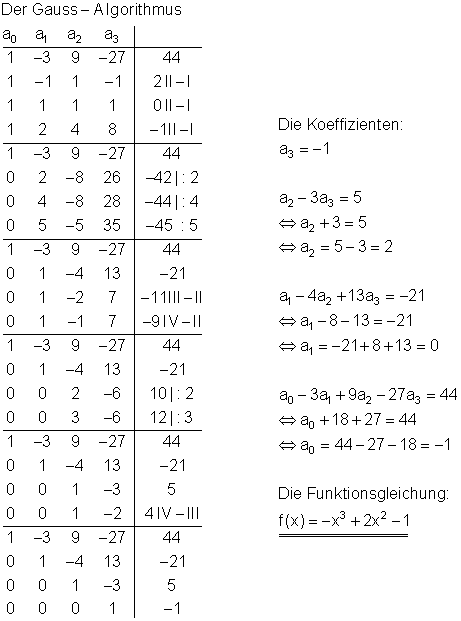
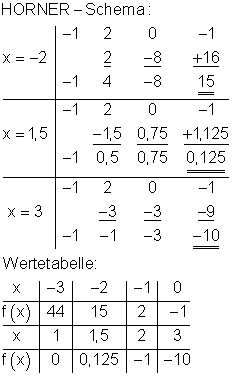
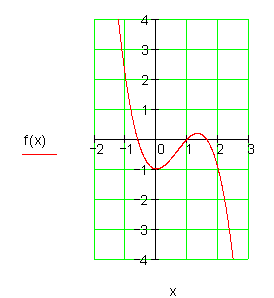
Schnittpunkt mit der y- Achse: Py( 0 | -1)
1. Nullstelle wird der Wertetabelle entnommen: Px1( 1 | 0 ).
Statt über die Polynomdivision kann man die weiteren Nullstellen über das Hornerschema bestimmen. Führt man die Berechnung für den x- Wert einer Nullstelle durch, dann erhält man die Koeffizienten für das Ergebnis der Polynomdivision.
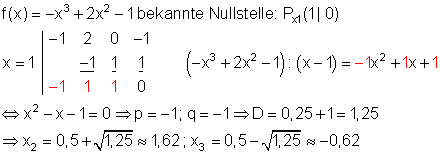
3. Bestimme den zugehörigen Funktionsterm
a) Ausführliche Lösung
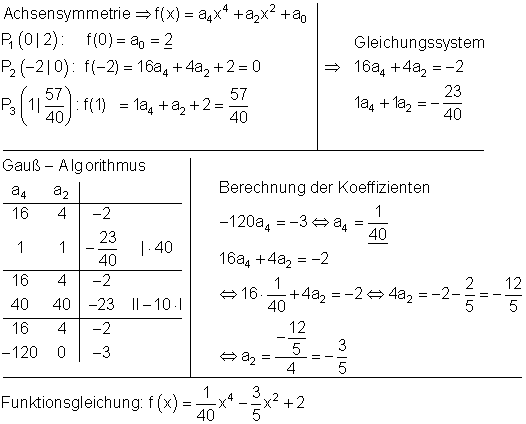
3. b) Ausführliche Lösung
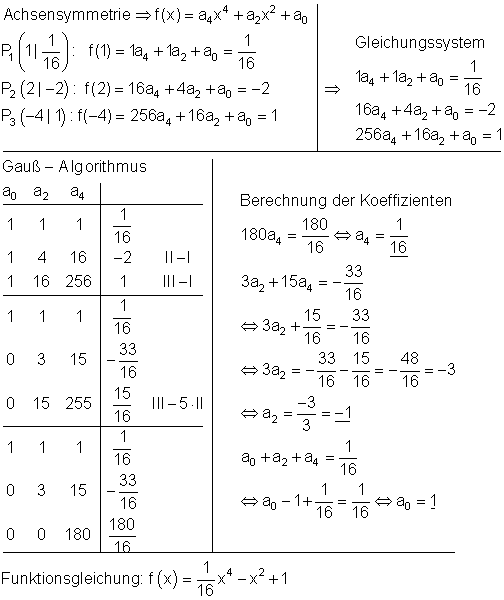
3. c) Ausführliche Lösung
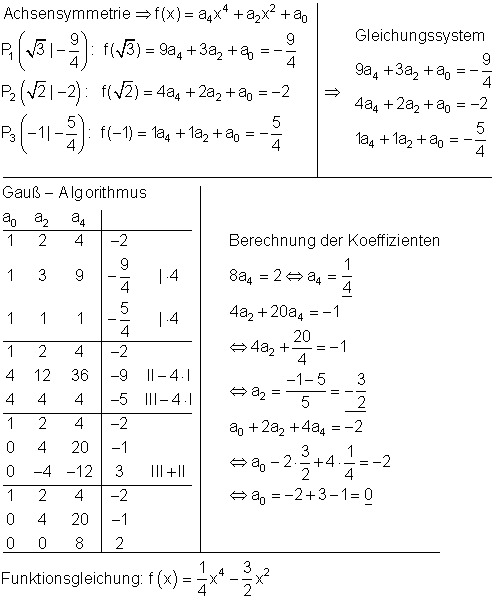
3. d) Ausführliche Lösung
4. Bestimme jeweils die Funktionsgleichung
a) Ausführliche Lösung
Das Gleichungssystem
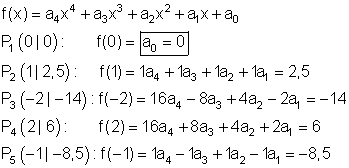
Der Gauß- Algorithmus:
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
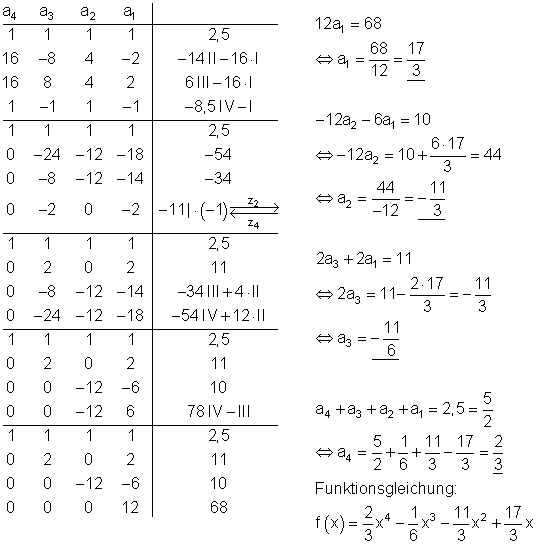
4. b) Ausführliche Lösung
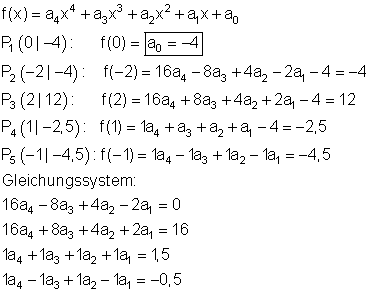
Gauß-Algorithmus.
Die Gleichungen können in beliebiger Reihenfolge eingesetzt werden.
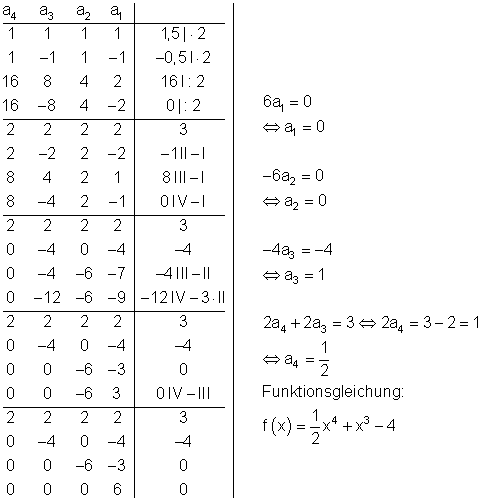
5. Bestimme jeweils die Funktionsgleichung
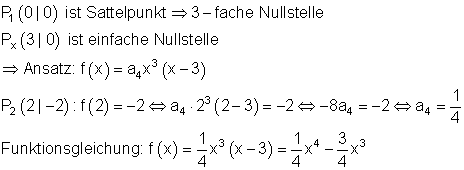
6. Bestimme die Funktionsgleichung f(x)
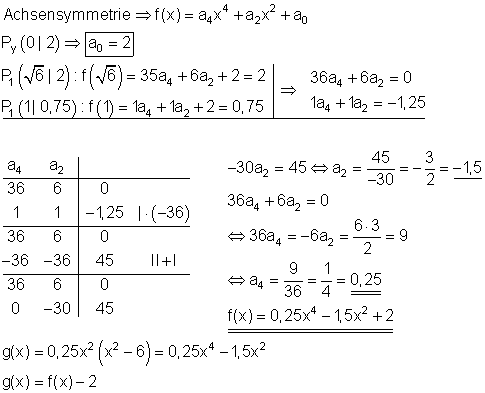
Die Funktion g(x) entsteht aus f(x) durch Verschiebung um 2 LE nach unten.
7. Bestimme einen möglichen Funktionsterm
Wir bestimmen die Funktionsgleichung für f*(x) mit der Bedingung 3 fache Nullstelle in x1 = 0 und einfache Nullstelle in x2 = 2.
Danach verschieben wir den Graphen um 3 LE nach oben bzw. nach unten, denn eine Parallele zur x- Achse vom Abstand 3 kann sowohl oberhalb als auch unterhalb der x- Achse verlaufen.

8. Zeige und zeichne
a)
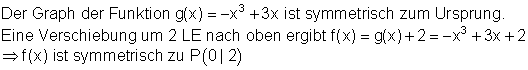
b)

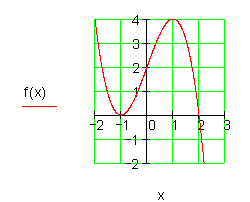
Dazu findest du hier die Aufgaben.
Und hier die Aufgaben Ganzrationale Funktionen gegebene Bedingungen IV.
Die Aufgaben Ganzrationale Funktionen aus gegebenen Bedingungen II und III sind in den Materialien enthalten, die man hier erwerben kann.
Die Theorie findest du hier: Aufstellen der Funktionsgleichung aus gegebenen Bedingungen.
Hier eine Übersicht über alle Beiträge zur weiteren ganzrationalen Funktionen.