Hier findest du die Lösungen der Aufgaben zu den Grundlagen der quadratischen Funktionen.
1. Zeichne die Graphen der folgenden Funktionen:
Ergebnisse
a) ![]()
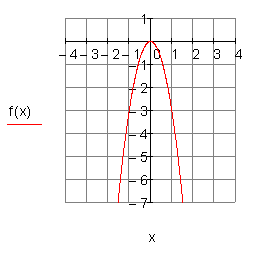
b) ![]()
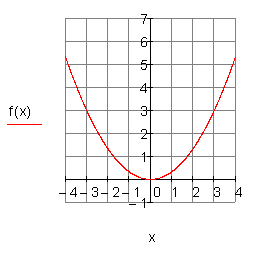
c) ![]()
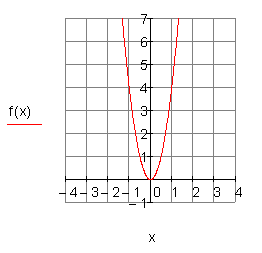
d) ![]()
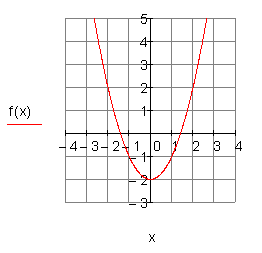
e) ![]()
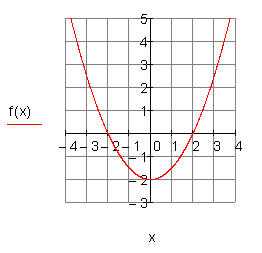
f) ![]()
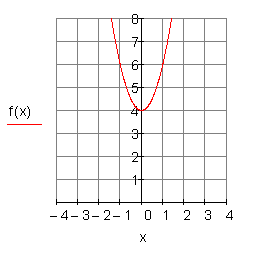
g) ![]()
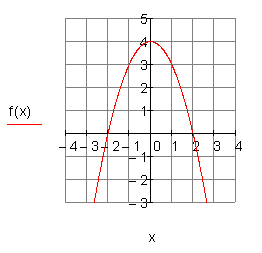
h) ![]()
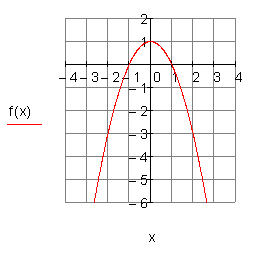
i) ![]()
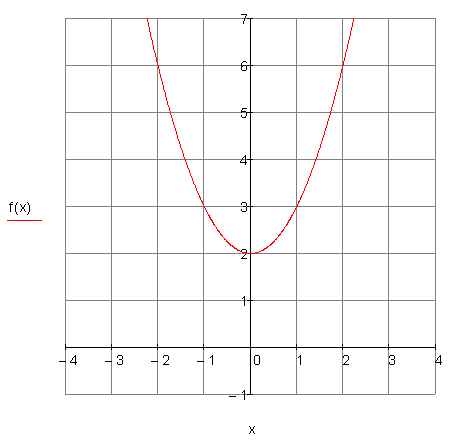
2. a) Berechne die Nullstellen,
die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis

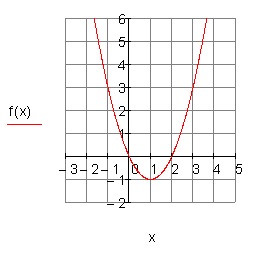
2. b)
Ergebnis
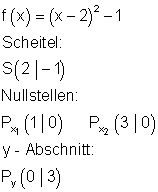
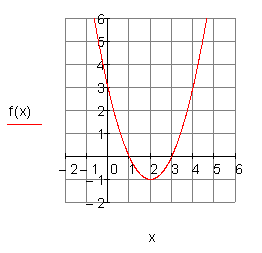
2. c) Ergebnis

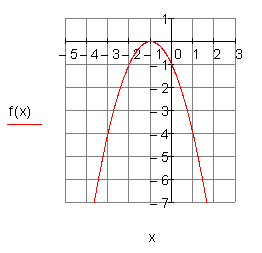
2. d) Ergebnis
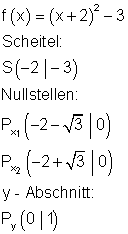
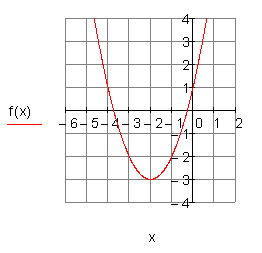
2. e) Ergebnis

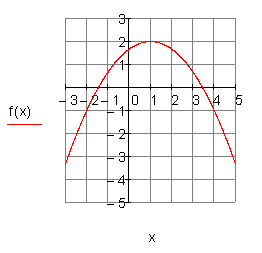
2. f) Ergebnis
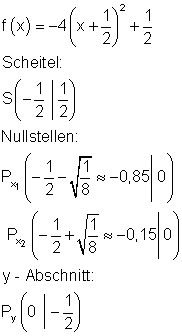
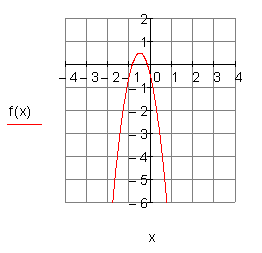
2. g) Ergebnis

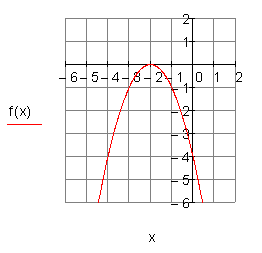
2. h) Ergebnis

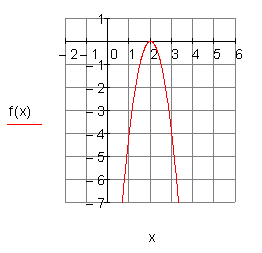
2. i) Ergebnis

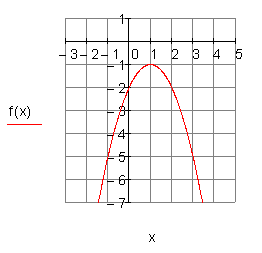
3. a) Berechne die Nullstellen,
die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis
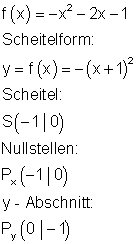
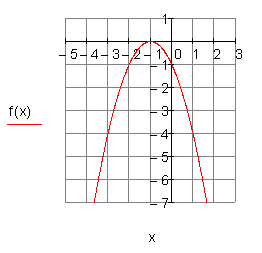
3. b)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis
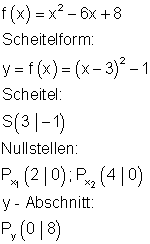
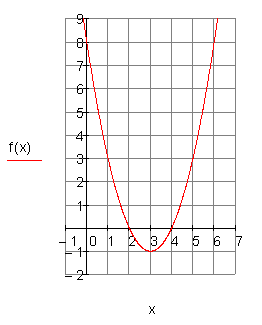
3. c)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis
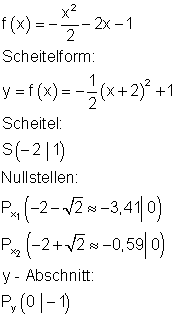
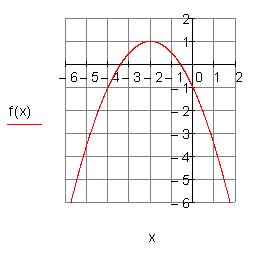
3. d)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis

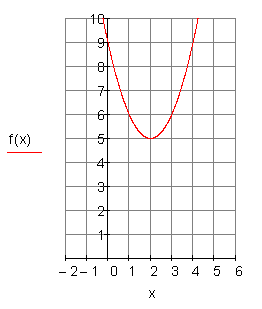
3. e)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis

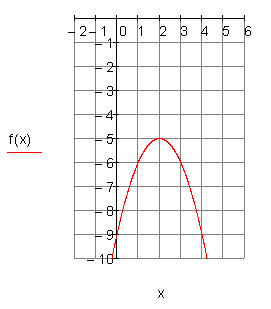
3. f)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis
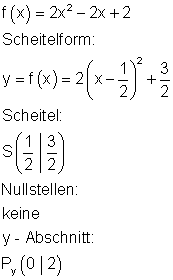
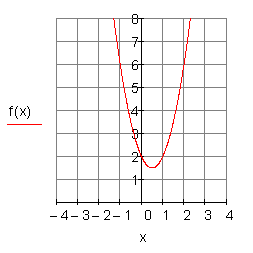
3. g)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis
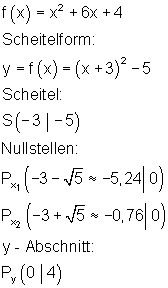
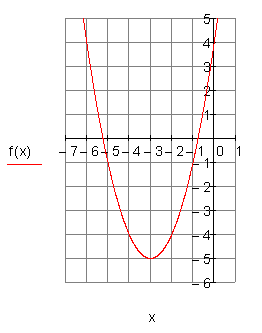
3. h)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis

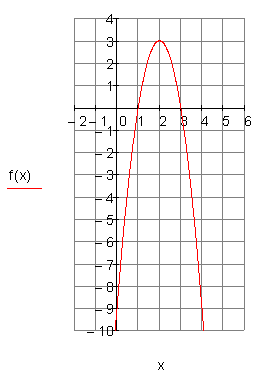
3. i)
Berechne die Nullstellen, die Achsenschnittpunkte, den Scheitelpunkt der Parabel und zeichne den Graphen in ein geeignetes Koordinatensystem.
Ergebnis

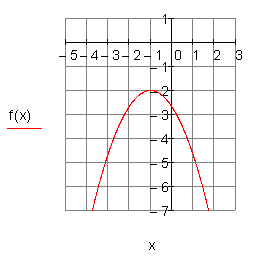
4. Zeichne die Parabeln
mit den angegebenen Funktionsgleichungen. Fertige dazu eine Wertetabelle an. Vergleiche die Graphen.
Ergebniss
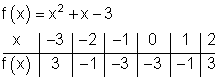
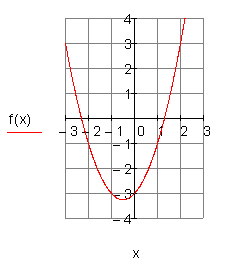
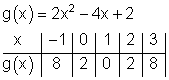
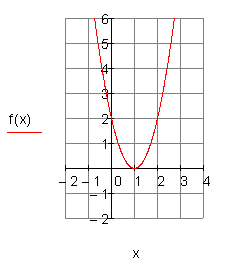
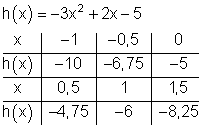
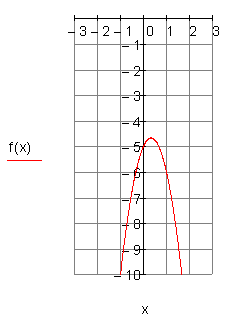
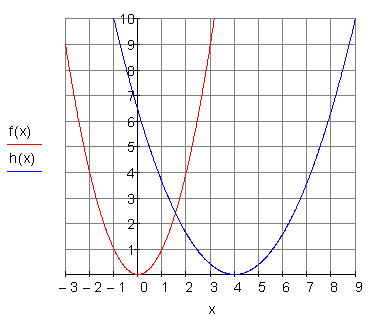
Die Graphen im Vergleich:
Die Graphen von f(x) und g(x) sind nach oben geöffnet.
Der Graph von h(x) ist nach unten geöffnet.
Die Graphen von g(x) und h(x) sind schlanker als der von f(x).
Das hat mit dem Formfaktor zu tun.
Der Graph von f(x) hat zwei Nullstellen,
der von g(x) eine doppelte Nullstelle
und der von h(x) hat keine Nullstelle.
5. Eine Normalparabel
wird mit dem Formfaktor 0,4 gestaucht und um 4 Einheiten nach rechts verschoben. Bestimme die Funktionsgleichung.
Ergebnisse

6. a) Gegeben ist eine Parabel
mit der Funktionsgleichung f(x). Verschiebe die Parabel in Richtung der y-Achse so, dass sie durch den Punkt P ( 0 | 2 ) geht. Zeichne beide Graphen in ein Koordinatensystem und bestimme die Funktionsgleichung g(x) der verschobenen Parabel.
Ergebnis

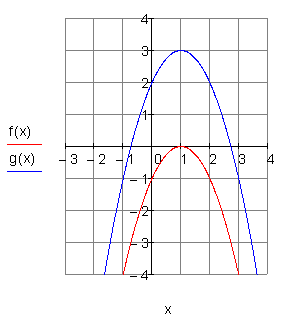
6. b)
Gegeben ist eine Parabel mit der Funktionsgleichung f(x). Verschiebe die Parabel in Richtung der y-Achse so, dass sie durch den Punkt P ( 0 | 2 ) geht. Zeichne beide Graphen in ein Koordinatensystem und bestimme die Funktionsgleichung g(x) der verschobenen Parabel.
Ergebnis
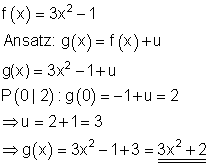
Die Parabel wird um 3 Einheiten nach oben geschoben
6. c)
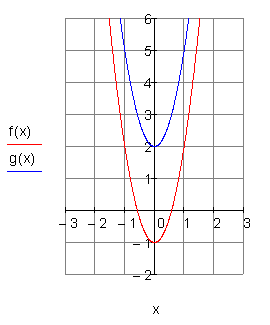
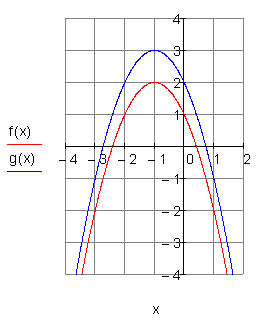
Gegeben ist eine Parabel mit der Funktionsgleichung f(x). Verschiebe die Parabel in Richtung der y-Achse so, dass sie durch den Punkt P ( 0 | 2 ) geht. Zeichne beide Graphen in ein Koordinatensystem und bestimme die Funktionsgleichung g(x) der verschobenen Parabel.
Ergebnis
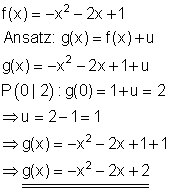
Die Parabel wird um 1 Einheit nach oben geschoben
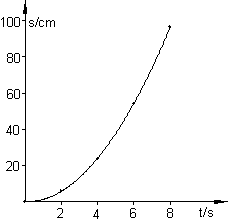
7. Ein physikalischer Versuch zeigt folgende Messwerte:
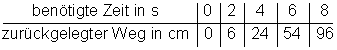
Trage die Werte in ein geeignetes Koordinatensystem ein und beschrifte die Achsen. Bestimme die Funktionsgleichung.
Ergebnis
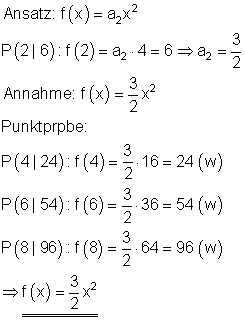
Hier findest du die Aufgaben.
hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen.
und hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.

