Hier findet ihr die ausführlichen Lösungen zu den Aufgaben Polynomgleichungen III. Einige Aufgaben enthalten Brüche, einige auch Wurzeln.
Dabei kann dir sicher eines dieser Videos helfen: Playlist aller Videos zu Polynomgleichungen.
1. Bestimme a so, dass die Gleichung (ax – 1)(x + 2)(x – 1/2) = 0 genau zwei Lösungen hat.
Ausführliche Lösung
Wie man aus den Linearfaktoren ablesen kann, hat die Polynomgleichung auf jeden Fall zwei Lösungen:
x1 = -2 und x2 = 1/2. Der Faktor a ist so zu bestimmen, dass keine neue Lösung hinzu kommen kann. Das ist dann der Fall, wenn es entweder bei den zwei Lösungen bleibt oder jeweils eine der vorhandenen Lösungen als Doppellösung dazu kommt.
Falls a = 0 ist, gilt: (- 1)(x + 2)(x – 1/2) = 0. In dem Fall bleiben die Lösungen unverändert.
Ansatz für eine dazukommende Doppellösung:
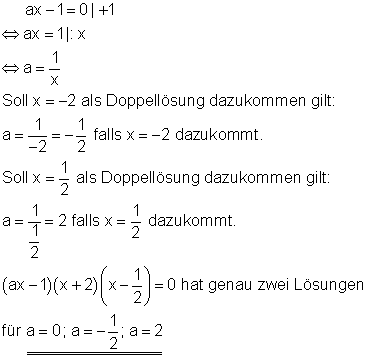
2. Eine Gleichung 3. Grades hat genau die beiden Lösungen L = { 2 ; -4 }
a) Mache Aussagen über die Art der Lösungen!
b) Gib zwei Gleichungen mit diesen Lösungen an!
Ausführliche Lösungen
a) Polynomgleichungen 3. Grades haben mindestens eine reelle Lösung. Die beiden weiteren Lösungen sind beide reell oder beide komplex. Da wir nur die reellen Lösungen betrachten wollen, bedeutet das für vorliegende Aufgabe, die genau zwei Lösungen haben soll, dass eine davon doppelt sein muss.
b) Sind für eine Polynomgleichung die Lösungen vorgegeben, so lassen sich über die Kombination von Linearfaktoren Gleichungen mit den gewünschten Eigenschaften konstruieren.
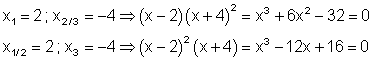
3. a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden, der da lautet:
„Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.“
Die Lösung der Gleichung findet man also dadurch, dass man jeden Faktor für sich gleich Null setzt.
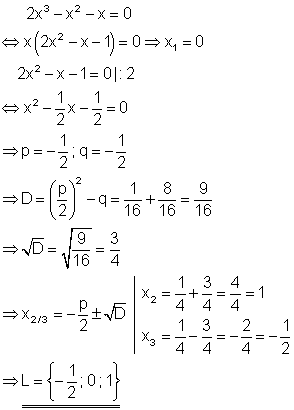
3. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Hat man die erste Lösung durch Reaten gefunden, so muss man auf jeden Fall die Polynomdivision durchführen um das Restpolynom zu finden. Hat man hingegen mit dem Horner-Schema einen Lösungswert für x gefunden, so lässt sich aus den Koeffizienten das Restpolynom bilden. Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision. Durch raten und probieren erhält man die Lösung x = -1.
Dazu kannst du dir das Video 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
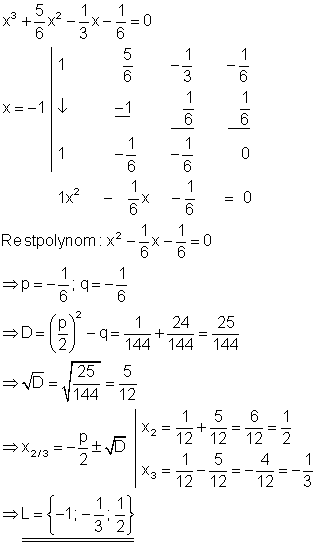
4. a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten erhält man die Lösung x = 2.
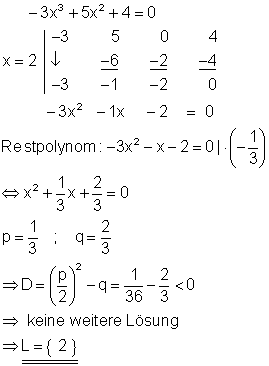
Die erste Zeile im Horner-Schema muss n + 1 Koeffizienten der Polynomgleichung enthalten, wenn der Polynomgrad n ist. Im obigen Beispiel fehlt in der Polynomgleichung der Summand mit dem Exponenten 1 also das x. Im Horner-Schema muss diese Stelle mit 0 aufgefüllt werden. Das Restpolynom hat keine Lösung, da die Diskriminante D < 0 ist.
4. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten erhält man die Lösung x = 1.
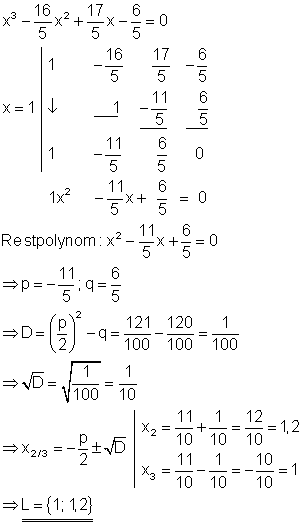
x = 1 ist doppelte Lösung, in der Lösungsmenge L tritt sie aber nur einmal auf.
5. a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten und probieren erhält man die Lösung x = 1.
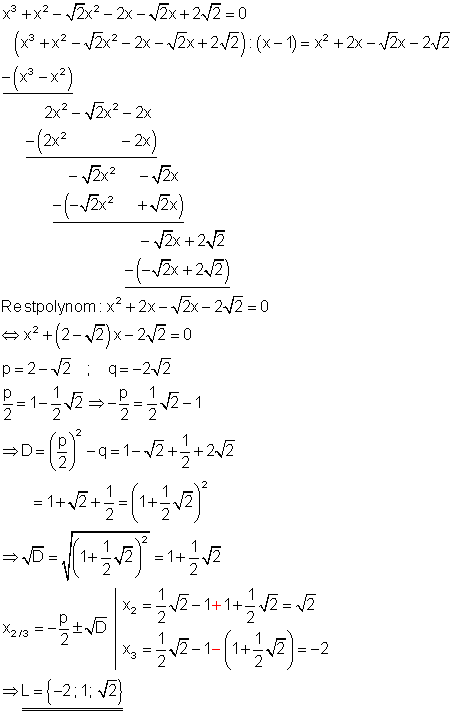
Um die quadratische Gleichung lösen zu können muss im Restpolynom durch ausklammern ein gemeinsamer Faktor für x gebildet werden, der das p für die p-q-Formel darstellt. Bei der weiteren Rechnung sollte man sicher in der Anwendung der binomischen Formeln sein.
5. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten und probieren erhält man die Lösung x = 1.
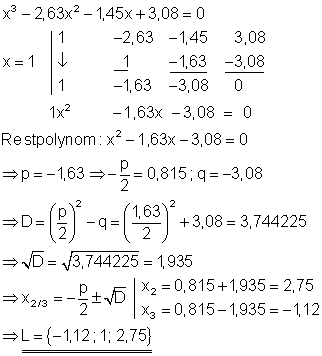
Zur Lösung der quadratischen Gleichung leistet der Taschenrechner gute Dienste.
6.
a) Löse die Gleichung nach u auf!
Ausführliche Lösung
Durch raten und probieren erhält man die Lösung u = 3/2.
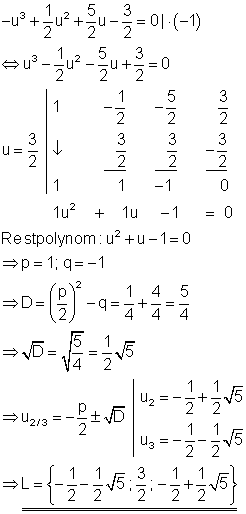
Es ist nicht immer einfach die erste Lösung durch raten und probieren zu finden. Teiler vom Absolutglied führen jedoch häufig zum Ziel (hier 3/2). Die Variable in der Gleichung muss auch nicht immer x sein, sie kann auch wie hier u genannt werden.
6. b) Löse die Gleichung nach a auf!
Ausführliche Lösung
Durch raten und probieren erhält man die Lösung a = 1.
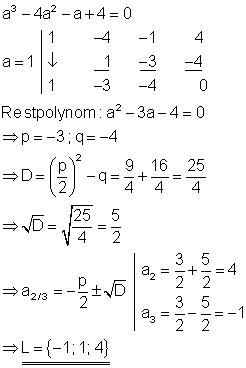
7.
a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x ausgeklammert werden. Lösung mit dem Satz vom Nullprodukt.
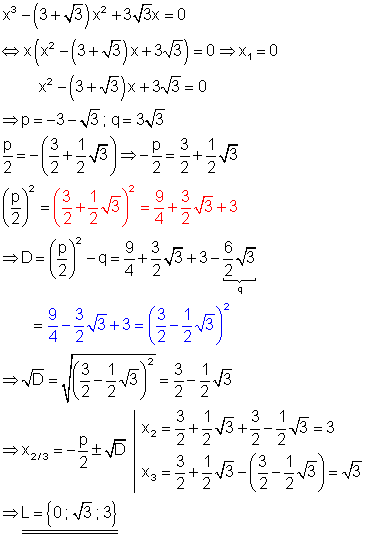
Beim quadrieren von p/2 kann das negative Vorzeichen vor der Klammer ignoriert werden, denn das Quadrat einer negativen Zahl ist positiv. Der Ausdruck der Diskriminante lässt sich mit der 2. binomischen Formel in ein Quadrat verwandeln, so dass die Wurzel der Diskriminante im Kopf lösbar ist.
7. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Lösung nach dem Satz vom Nullprodukt.
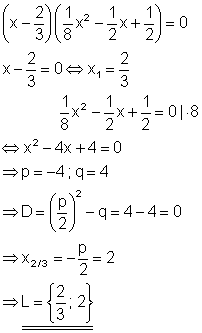
8.
a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten und probieren erhält man die Lösung x = -1.
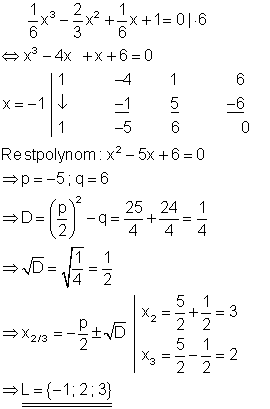
8. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
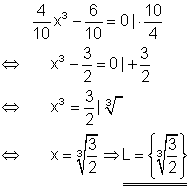
9.
a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden.
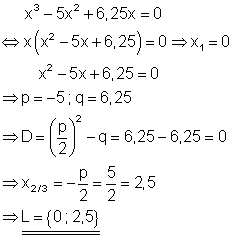
9. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x2 ausgeklammert werden. Lösung nach dem Satz vom Nullprodukt.
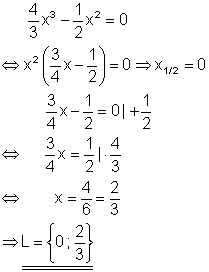
10.
a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Aus der Polynomgleichung kann x ausgeklammert werden. Lösung nach dem Satz vom Nullprodukt.
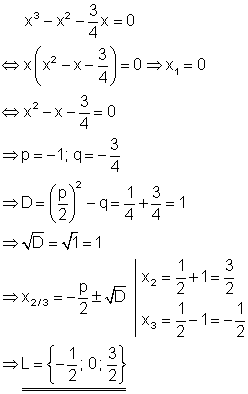
10. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten erhält man die Lösung x = 2.
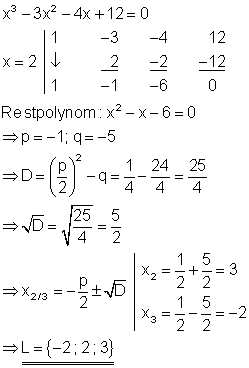
11.
a) Löse die Gleichung nach x auf!
Ausführliche Lösung
Durch raten erhält man die Lösung x = -1.
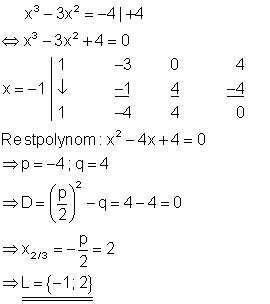
11. b) Löse die Gleichung nach x auf!
Ausführliche Lösung
Lösung nach dem Satz vom Nullprodukt.
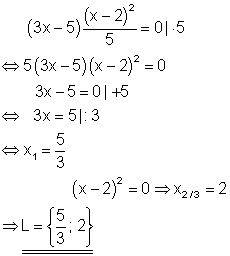
Hier findest du die Aufgaben.
Und hier die Theorie Polynomgleichungen
Hier weitere Aufgaben Polynomgleichungen VII.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

