In diesem Beitrag finden Sie ausführlichen Lösungen zu den Aufgaben Polynomgleichungen IV mit Parametern. Z. B.: Für welche Werte von a hat die Gleichung eine Lösung, genau zwei oder drei Lösungen?
Dabei kann dir sicher eines dieser Videos helfen: Playlist aller Videos zu Polynomgleichungen.
1. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Hat man die erste Lösung durch Reaten gefunden, so muss man auf jeden Fall die Polynomdivision durchführen um das Restpolynom zu finden. Hat man hingegen mit dem Horner-Schema einen Lösungswert für x gefunden, so lässt sich aus den Koeffizienten das Restpolynom bilden. Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision. Durch raten und probieren erhält man die Lösung x = -2.
Dazu kannst du dir das Video 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
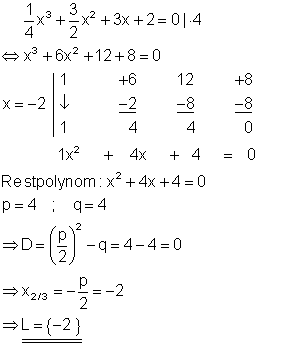
Da die Diskriminante der quadratischen Gleichung Null ist, hat diese nur eine (doppelte) Lösung und zwar ebenfalls x = -2, wie man bereits geraten hat. In der Lösungsmenge wird auch nur die -2 als Lösung angegeben. Insgesamt handelt es sich um eine dreifache Lösung.
1. b.)
Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Durch raten erhält man die Lösung x = -1.
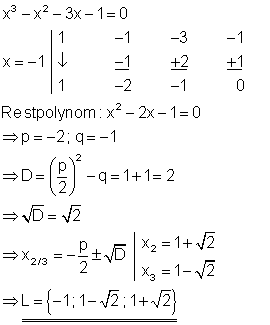
2. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Durch Raten erhält man die Lösung x = 1.

2. b)
Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Durch Raten erhält man die Lösung x = 3.

Die erste Zeile im Horner-Schema muss n + 1 Koeffizienten der Polynomgleichung enthalten, wenn der Polynomgrad n ist. Im obigen Beispiel fehlt in der Polynomgleichung der Summand mit dem Exponenten 1 also das x. Im Horner-Schema muss diese Stelle mit 0 aufgefüllt werden. Das Restpolynom hat keine Lösung, da die Diskriminante D < 0 ist.
3. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Durch Raten erhält man die Lösung x = 3.
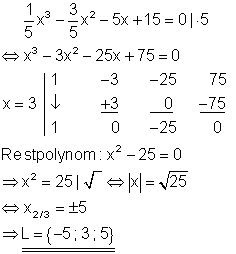
3. b)
Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Durch Raten erhält man die Lösung x = -1.
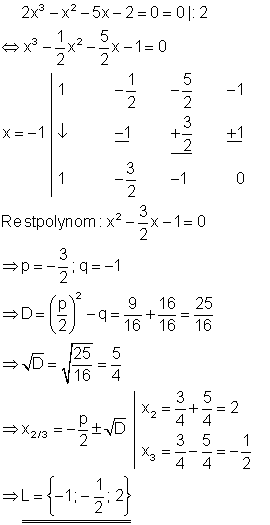
4. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
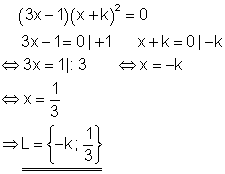
Da die zweite Klammer in Form eines Quadrates auftritt, ist -k eine doppelte Lösung.
4. b)
Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
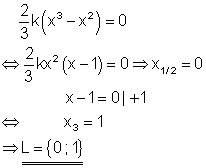
Die Formvariable k hat keinen Einfluss auf die Lösung.
5. a) Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
Aus der Polynomgleichung kann x ausgeklammert werden. Es entsteht ein Produkt. Da dieses aber Null ist, kann der Satz vom Nullprodukt angewendet werden, der da lautet: „Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.“ Die Lösung der Gleichung findet man also dadurch, dass man jeden Faktor für sich gleich Null setzt.
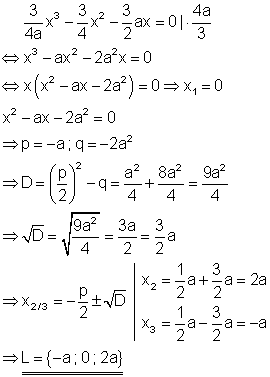
5. b)
Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
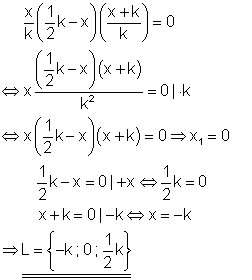
6. a) Berechnen Sie die Lösungen folgender Gleichung!
Ausführliche Lösung
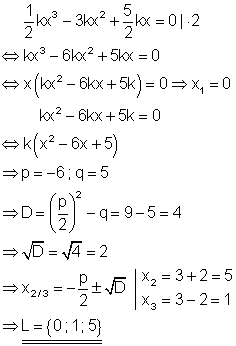
6. b)
Berechne die Lösungen folgender Gleichung!
Ausführliche Lösung
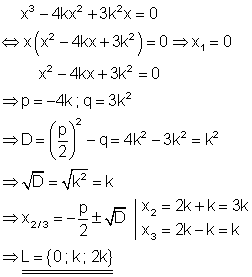
7. Bestimme die Lösungen!
Ausführliche Lösung
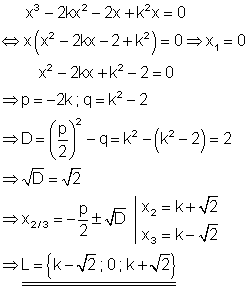
8. Löse die Gleichung nach x auf.
Für welche Werte von k gibt es nur eine Lösung?
Ausführliche Lösung
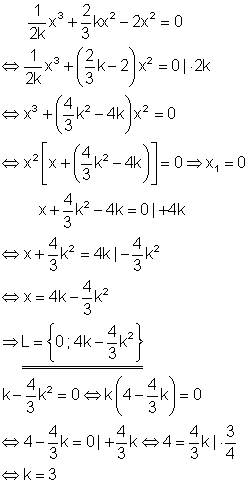
Die Lösung x1 = 0 existiert unabhängig von k. Für alle anderen Werte von k gibt es zwei Lösungen, mit Ausnahme von k = 3.
9. Für welche Werte von a
hat die Gleichung eine Lösung, genau zwei oder drei Lösungen?
Ausführliche Lösung
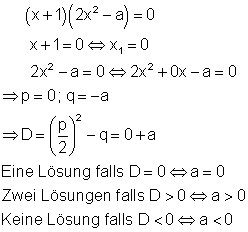
Für die Gesamtlösung bedeutet das:
Eine Lösung gibt es immer (erste Klammer = 0, x1 = -1).
Die quadratische Gleichung kann in Abhängigkeit von der Diskriminante eine, zwei oder keine Lösung haben.
Falls a < 0 ist, hat die Polynomgleichung nur eine Lösung L = { -1 }.
Falls a = 0 ist, hat die Polynomgleichung zwei Lösungen L = { -1 ; 0 }.
Falls a > 0 ist, hat die Polynomgleichung drei Lösungen.
Damit in diesem Fall auch wirklich 3 unterschiedliche Lösungen vorliegen, darf die Lösung x1 = -1 nur einmal vorkommen. Zu untersuchen ist also für welche Werte von a die zweite Klammer bei dem x-Wert -1 Null wird.

10. Untersuche die Lösungen in Abhängigkeit von a!
Ausführliche Lösung
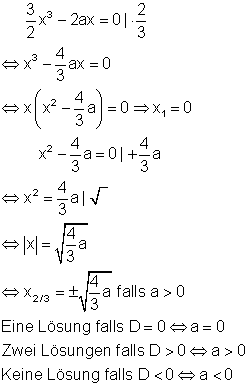
Falls a = 0 ist, gibt es nur eine Lösung L = {0}.
Nun werden die Lösungen der quadratischen Gleichung in Zusammenhang mit der Formvariablen a betrachtet.
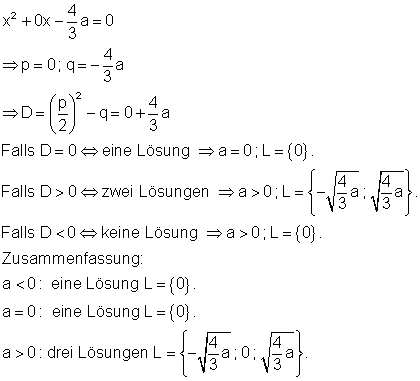
11. Untersuche die Lösungen in Abhängigkeit von a!
Ausführliche Lösung
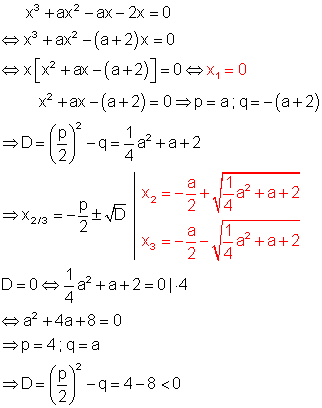
Aus dem Term lässt sich x ausklammern, so dass nach dem Satz vom Nullprodukt die Lösungen zu bestimmen sind. Die Lösung x1 = 0 gilt unabhängig von a. Die Diskriminante der quadratischen Gleichung kann, wie die Rechnung zeigt nicht Null werden, damit auch nicht kleiner als Null. Das bedeutet, die quadratische Gleichung hat für jedes a genau zwei Lösungen. Es ist lediglich zu überprüfen ob für einen bestimmten Wert von a die Lösung der quadratischen Gleichung 0 ergibt. In diesem Fall hätte die Polynomgleichung insgesamt nur 2 Lösungen.
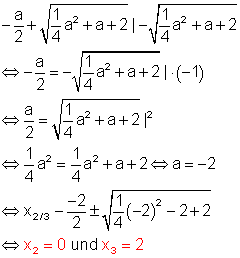
Spezialfall: Falls a = -2 ist, hat die Polynomgleichung genau 2 Lösungen.
12. Untersuche die Lösungen in Abhängigkeit von k!
Ausführliche Lösung
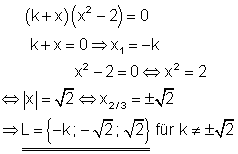
Falls k einen der Wurzelwerte annimmt, verringert sich die Anzahl von Lösungen von drei auf zwei.
13. Die Lösung einer Gleichung 3. Grades sind 2/3, 3/4, und -2.
Gib eine Polynomgleichung mit ganzzahligen Koeffizienten an!
Ausführliche Lösung
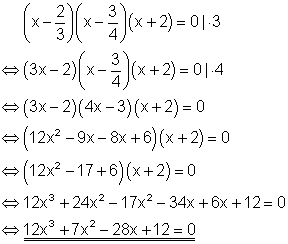
Zuerst stellt man anhand der vorgegebenen Lösungen die Polynomgleichung als Produkt ihrer Linearfaktoren auf. Um eine Polynomgleichung mit ganzzahligen Koeffizienten zu bekommen multipliziert man nun beide Seiten der Gleichung mit den Nennern der Brüche in den Linearfaktoren. Dabei darf immer nur ein Linearfaktor multipliziert werden. Sobald in den Linearfaktoren keine Brüche mehr auftreten, multipliziert man diese aus und erhält die gesuchte Polynomgleichung.
Hier findest du die Aufgaben.
Und hier weitere und Aufgaben Polynomgleichungen VI mit Parametern.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.

