Hier findest du die Lösungen zu weiteren Aufgaben zu Verknüpfungen von Ereignissen. Diesmal geht es auch um Gegenereignisse.
1. Aufgabe
Ein Würfel wird einmal geworfen. Folgende Ereignisse werden definiert:
A: Die geworfene Zahl ist kleiner als 4.
B: Die geworfene Zahl ist ungerade.
Bestimme folgende Ereignisse in aufzählender Form:
a) A ∪ B b) A ∩ B c) \bar A \cap \bar B d) \overline{A \cap B} e) A \cap \bar B f) \overline{A \cup B}
Dazu kannst du dir das 📽️Video Ereignisse in der Wahrscheinlichkeitsrechung ansehen.
1. Ausführliche Lösungen:
S = {1; 2; 3; 4; 5; 6} A = {1; 2; 3} B = {1; 3; 5}
a) A ∪ B = {1; 2; 3; 5}
b) A ∩ B = {1; 3}
c) \bar A = S \ A = {4; 5; 6}
\bar B = S \ B = {2; 4; 6}
\Rightarrow \bar A \cap \bar B = {4; 6}
d) A ∩ B = {1; 3}
\Rightarrow \overline{A \cap B} = S \ A ∩ B = {2; 4; 5; 6}
e) \bar B = {2; 4; 6}
\Rightarrow A \cap \bar B = {2}
f) \overline{A \cup B} = S \ A \cup B = {4; 6}
2. Aufgabe
Eine Urne enthält 3 rote und 5 schwarze Kugeln. Aus der Urne werden nacheinander drei Kugeln ohne zurücklegen entnommen. Folgende Ereignisse werden definiert:
A: Die ersten zwei gezogenen Kugeln haben unterschiedliche Farbe.
B: Die zuerst und die zuletzt gezogene Kugel haben dieselbe Farbe.
a) Zeichne das Baumdiagramm und gib die Ergebnismenge an.
b) Gib folgende Ereignisse in aufzählender Form an:
A; \quad B; \quad A \cap B; \quad \bar A; \quad A \cup \bar B
2. Ausführliche Lösungen:
a)
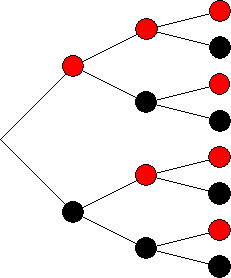
Ergebnismenge: S = {rrr; rrs; rsr; rss; srr; srs; sss}
b)
S = {rrr; rrs; rsr; rss; srr; srs; sss}
A = {rsr; rss; srr; srs}
B = {rrr; rsr; srs; sss}
A ∩ B = {rsr; srs}
\bar A = S \ A = {rrr; rrs; ssr; sss}
\bar B = S \ B = {rrs; rss; srr; ssr}
\Rightarrow A \cup \bar B = {rsr; rss; srr; srs; rrs; ssr}
3. Aufgabe
In einer Lostrommel befinden sich noch 15 Lose, davon sind 10 Lose Nieten. Aus der Lostrommel werden nacheinander 2 Lose gezogen. Folgende Ereignisse werden definiert:
A: Es werden nur Nieten gezogen.
B: Genau ein Gewinnlos wird gezogen.
C: Das zuletzt gezogene Los ist eine Niete.
a) Zeichne das Baumdiagramm und gib die Ergebnismenge an.
b) Bestimme die Ereignisse D = \overline{A \cup B} \quad und \quad E = B \cap \bar C
3. Ausführliche Lösungen:
a)
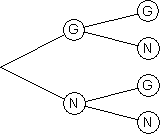
Ergebnismenge: S = {GG; GN; NG; NN}
b)
Ergebnismenge: S = {GG; GN; NG; NN}
A = {NN} B = {GN; NG} C = {GN; NN}
A ∪ B = {NN; GN; NG}
D = \overline{A \cup B} = S \ A \cup B = {GG}
\bar C = {GG; NG}
E = B \cap \bar C = {NG}
4. Aufgaben
Von zwei Ereignissen A und B weiß man, dass A \cup B = S und A \cap B = \varnothing
Was kann man über die Ereignisse A und B aussagen?
4. Ausführliche Lösung:
A und B sind unvereinbar. S \ B = A => B ist das Gegenereignis von A.
5. Aufgabe:
Aus einer Urne mit 100 gleichartigen, von 1 bis 100 nummerierten Kugeln wird eine Kugel gezogen. Folgende Ereignisse werden definiert:
A: Die Zahl ist durch 8 teilbar.
B: Die Zahl ist durch 15 teilbar.
C: Die Zahl ist durch 8 oder durch 9 teilbar.
D: Die Zahl ist durch 9 oder durch 15 teilbar.
E: Die Zahl ist durch 12 oder durch 15 teilbar.
F: Die Zahl ist durch 12 oder durch 17 teilbar.
G: Die Zahl ist durch 8 aber nicht durch 12 teilbar.
H: Die Zahl ist durch 12 aber nicht durch 8 teilbar.
Bestimme alle Ergebnismengen in aufzählender Form.
5. Ausführliche Lösung:
S = { 1; 2; ….. 99; 100}
A = { 8; 16; 24; 32; 40; 48; 56; 54; 72; 80; 88; 96 }
B = { 15; 30; 45; 60; 75; 90 }
C = { 8; 9; 16; 18; 24; 27; 32; 36; 40; 45; 48; 54; 56; 63; 64; 72; 80; 81; 88; 90; 96; 99 }
D = { 9; 15; 18; 27; 30; 36; 45; 54; 60; 63; 72; 75; 81; 90; 99 }
E = { 12; 15; 24; 30; 36; 45; 48; 60; 72; 75; 84; 90; 96 }
F = { 12; 17; 24; 34; 36; 48; 51; 60; 68; 72; 84; 85; 96 }
G = { 8; 16; 32; 40; 56; 64; 80; 88 }
H = { 12; 36; 60; 84 }
Hier findest du die Aufgaben hierzu.
Theorie hierzu: Ereignisse in der Wahrscheinlichkeitsrechnung.
Verknüpfung von Ereignissen in der Wahrscheinlichkeitsrechnung.
Standardmengen und mathematische Zeichen.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.

