Hier findest du eine Zusammenfassung der wichtigen Grundbegriffe aus der Statistik, eine Statistik Formelsammlung:
- Stichprobe, Urliste, Rohdaten, Erhebungsumfang
- Klasseneinteilung
- Häufigkeit und Häufigkeitsdichte im Histogramm
- Vergleich Säulendiagramm und Histogramm
- Median, Modalwert, Spannweite, Quartile und Quartilsabstand
- Varianz und Standardabweichung
- Links zu weiteren Beiträgen
Stichprobe:
Wird der Teil einer Gesamtheit befragt, dann spricht man bei der Datenerhebung von einer Stichprobe.
Urliste:
Das Ergebnis der Stichprobe wird in einer Urliste festgehalten.
Rohdaten:
Sind alle in der Urliste enthaltenen Daten.
Erhebungsumfang:
Ist die Anzahl der untersuchten Objekte.
Werden z.B. 27 Schüler befragt, so sagt man, „Die Anzahl der Merkmalsträger ( n = 27 ) bildet den Erhebungsumfang“.
Merkmale:
Sind die Eigenschaften der Objekte. (z.B. Geschlecht, Körpergröße, Gewicht, Raucher, Sportart, …)
Merkmalsausprägung:
Ein Merkmal kann in verschiedenen Ausprägungen vorkommen. (z.B. Geschlecht m oder w).
Klasseneinteilung:
Werden verschiedene Merkmalsausprägungen zu einer neuen Ausprägung zusammengefasst, so spricht man von einer Klasseneinteilung der Stichprobenwerte. Die Darstellung erfolgt in einem Säulendiagramm ohne Lücken.
Häufigkeiten:
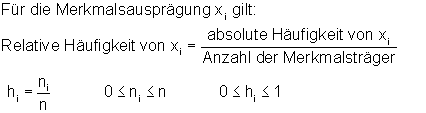
Häufigkeitsdichte im Histogramm:
![]()
Vergleich von Säulendiagramm und Histogramm
Säulendiagramm
Wenn man die relativen Häufigkeiten als Längen von Säulen veranschaulicht,entsteht ein Säulendiagramm.
Die Summe der Längen aller Säulenhat den Wert 1 (100%)
Histogramm
Wenn man die relativen Häufigkeiten als Flächen von Rechtecken veranschaulicht, entsteht ein Histogramm.
Die Summe der Flächeninhalte hat den Wert 1 (100%)
Arithmetisches Mittel einer Datenreihe
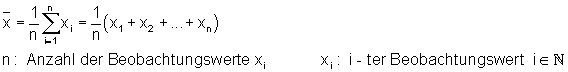
Der Median (Zentralwert einer Datenreihe):
Der Median xMed ist derjenige Wert (Merkmalsausprägung), der in der Mitte steht, wenn alle Beobachtungswerte xi der Größe nach geordnet sind.
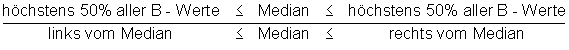
Allgemeine Rechenvorschrift zur Berechnung des Medians:

Modalwert (Modus):
Der Modalwert xMod ist der Merkmalswert, der am häufigsten vorkommt.
Die Spannweite:
![]()
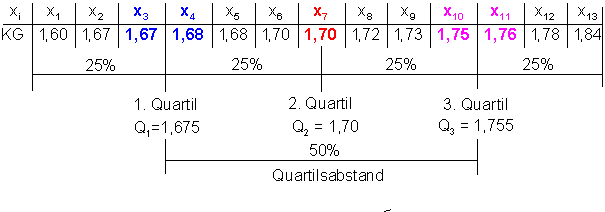
Quartile und Quartilsabstand.
![]()
Varianz und Standardabweichung einer Datenreihe:
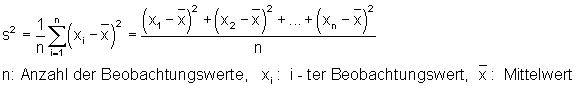
![]()


