Im letzten Beitrag haben wir uns mit dem Kreisdiagramm beschäftigt. Hier werde ich zuerst die gleiche und unterschiedliche Klassenbreite in der Häufigkeitstabelle erklären. Danach die unterschiedliche Säulenbreite in der graphischen Darstellung. Schließlich werde ich Säulendiagramm und Histogramm vergleichen. Dies alles erläutere ich anhand anschaulicher Beispiele.
- Gleiche und unterschiedliche Klassenbreite in der Häufigkeitstabelle
- Unterschiedliche Säulenbreite in der graphischen Darstellung
- Säulendiagramm und Histogramm vergleichen
Häufigkeitstabelle
Beispiel: gleiche Klassenbreite in der Häufigkeitstabelle
Schauen wir uns dazu einen Betrieb A an, der die Monatsverdienste seiner Mitarbeiter auflistet. Dabei teilt diese Firma in gleich große Klassen ein. Z. B. von ≤ 800 € bis < 1000 € und von ≤ 1000 € bis < 1200 €. Die Differenz beträgt also immer 200 €.
Häufigkeitstabelle:
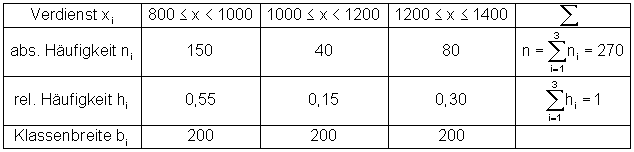
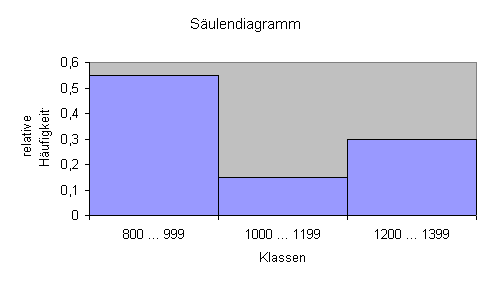
Bei gleicher Klassenbreite ist die graphische Darstellung einer relativen Häufigkeitsverteilung ein Säulendiagramm.
Die Summe der Säulenlängen ergibt dann den Wert 1 (100%).
Es besteht aus mehreren direkt aneinander angrenzenden Säulen, deren Flächeninhalt proportional zur relativen Klassenhäufigkeit ist.
Beispiel: unterschiedliche Klassenbreite in der Häufigkeitstabelle
Ein Betrieb B hat dagegen die Monatsverdienste seiner Mitarbeiter wie folgt aufgelistet. Z. B. von ≤ 800 € bis < 1000 € beträgt die Differenz 200 €. Von ≤ 1000 € bis < 2000 € sind es allerdings 1000 €. Diese Firma teilt also in unterschiedlich große Klassen ein.
Häufigkeitstabelle:
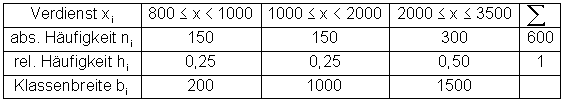
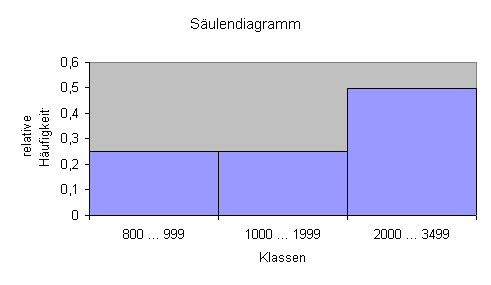
Bei diesem Diagramm wurde die gleiche Säulenbreite gezeichnet, obwohl es sich um unterschiedliche Klassenbreiten handelt.
Die Summe der Säulenlängen ergibt dennoch den Wert 1 (100%).
Die Flächeninhalte sind jedoch nicht proportional zur relativen Klassenhäufigkeit.
Unterschiedliche Säulenbreite in der graphischen Darstellung
Diagramm für die Monatsverdienste bei unterschiedlicher Klassenbreite. Weil die Klassen unterschiedlich groß sind, hat man die Säulen entsprechend breit gezeichnet.
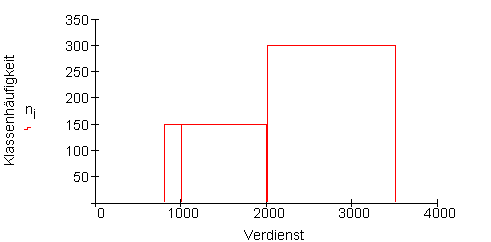
Beim Betrachten dieses Diagramms entsteht der Eindruck, dass die Häufigkeit für die Klasse 800 … 999 kleiner ist als für die Klasse 1000 … 1999.
Denn das Auge orientiert sich an der Größe der Recheckflächen und nicht an deren Höhe.
Daher ist diese Darstellung unzweckmäßig.
Es ist deshalb sinnvoller, ein Diagramm zu wählen, bei dem der Rechteckinhalt der Klassenhäufigkeit entspricht.
Dazu muss die jeweilige Rechteckhöhe berechnet werden.
Das Histogramm
![]()
Für unser Beispiel bedeutet das, man muss die erste Säule höher zeichnen.
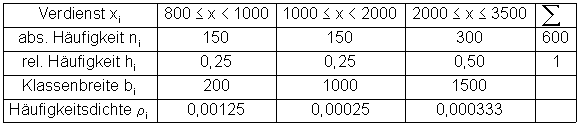
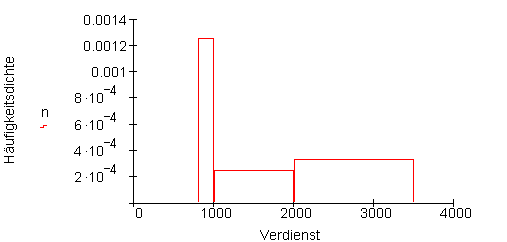
Eine solche graphische Darstellung wird Histogramm genannt.
Was genau sind Histogramme?
In Histogrammen werden relative Häufigkeiten durch Flächeninhalte von Rechtecken dargestellt.
Die Rechteckhöhe heißt dabei Häufigkeitsdichte.

Multipliziert man die Häufigkeitsdichte mit der Intervallbreite, erhält man dadurch die relative Häufigkeit.
Vergleich von Säulendiagramm und Histogramm
Wenn man die relativen Häufigkeiten als Längen von Säulen veranschaulicht, entsteht ein Säulendiagramm.
Die Summe der Längen aller Säulenhat den Wert 1 (100%) Histogramm
Wenn man die relativen Häufigkeiten als Flächen von Rechtecken veranschaulicht, entsteht ein Histogramm.
Die Summe der Flächeninhalte hat dabei den Wert 1 (100%)
Im ersten Beitrag zur Statistik Datenerhebung und Darstellung hatten wir gesehen, dass Merkmale die Eigenschaften der Objekte sind. Beispiele hierfür sind Geschlecht, Körpergröße, Gewicht, Raucher, Sportart. Im nächsten Beitrag werden wir sehen, dass es unterschiedliche Merkmalsarten gibt.
Hier findest du die Aufgaben hierzu: Merkmale
Hier findest du eine Übersicht über alle Beiträge zum Thema Statistik, dort auch Links zu weiteren Aufgaben.
Alle Formeln zur beschreibenden Statistik sind hier übersichtlich zusammengestellt.


