Wir haben uns bisher den Schnittpunkt von Parabel und Gerade berechnet. In diesem Beitrag erkläre ich zuerst, wie man die Funktionsgleichung der Parabel durch drei Punkte aufstellt. Danach zähle ich die Reihenfolge in der Vorgehensweise beim Aufstellen auf. Dann zeige ich das Aufstellen des Gleichungssystems und das Additionsverfahrens. Außerdem stelle ich ein interaktives Programm zur Verfügung. Danach zeige ich, wann man die Funktionsgleichung einer Parabel mit weniger Angaben bestimmen kann. Zuletzt zeige ich ein Anwendungsbeispiel.
Wenn wir drei unterschiedliche Punkte kennen, die auf einer Parabel liegen. Daraus sollen wir die Funktionsgleichung der Parabel bestimmen. Wie gehen wir nun vor?
Vorgehensweise beim Aufstellen einer Gleichung für eine Parabel durch drei Punkte:
1. Stelle zuerst das Gleichungssystem auf.
2. Löse dann dieses mit Hilfe des Gauß Algorithmus.
3. Bestimme anschließend die Koeffizienten von f(x) durch einsetzen.
4. Schreibe danach die Funktionsgleichung hin und machen Sie die Probe.
5. Berechne schließlich die Achsenschnittpunkte und den Scheitelpunkt.
6. Zeichne zuletzt die Parabel in ein geeignetes Koordinatensystem.
Die allgemeine Form der Funktionsgleichung einer ganzrationalen Funktion 2. Grades lautet:
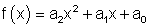
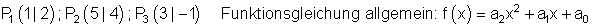
Zuerst müssen wir für die allgemeinen Koeffizienten a2, a1 und a0 die entsprechenden Zahlenkomponenten bestimmen.
Weil alle drei gegebenen Punkte P1 , P2 und P3 Punkte der zu bestimmenden Parabel sind, können wir durch dreimaliges Einsetzen der Koordinaten dieser Punkte an den Stellen x und y der allgemeinen Funktionsgleichung ein Gleichungssystem aus drei Gleichungen mit drei Unbekannten erzeugen. Aus diesen können wir anschließend die Koeffizienten a0, a1 und a2 bestimmen.
Dazu kannst du dir das 📽️Video Funktionsgleichung Parabel durch drei Punkte ansehen.
Aufstellen des Gleichungssystems:
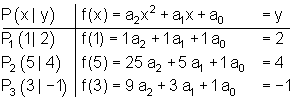
Das ist ein Gleichungssystem bestehend aus drei linearen Gleichungen mit drei Unbekannten. Deshalb können wir die Lösung mit dem Additionsverfahren finden.
Additionsverfahren:
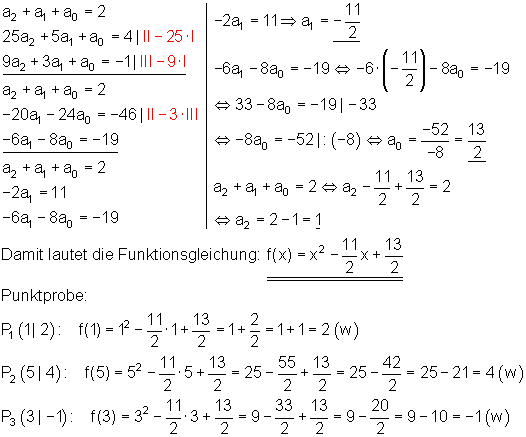
Das Additionsverfahren können wir schematisieren. Dies benutzen wir ebenfalls beim Gauß-Algorithmus. Beim Gauß-Algorithmus rechnet man allerdings nur mit den Koeffizienten.
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
Gauß-Algorithmus:
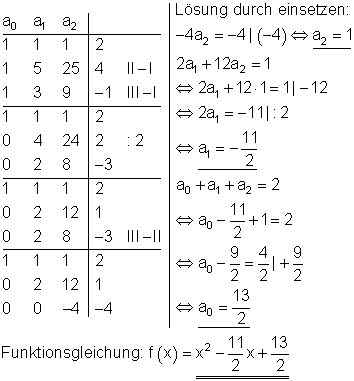
Beim Gauß-Algorithmus arbeiten wir zeilenweise.
Dabei darf man Zeilen:
– vertauschen
– mit einer Zahl multiplizieren
– durch eine Zahl dividieren
– addieren
– subtrahieren
Wenn wir die Spalten vertauschen, dann müssen wir ebenfalls die Koeffizienten mitnehmen.
Dabei versuchen wir, auf eine Dreiecksform zu kommen.
Der Funktionsgraph:
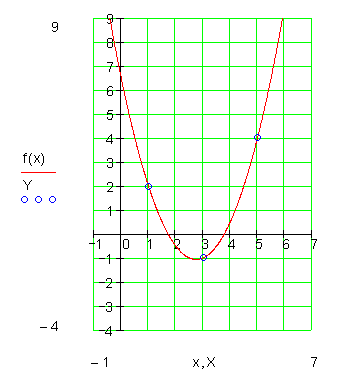
Um die Funktionsgleichung einer quadratischen Funktion zu erhalten brauchen wir drei Punkte .
Wir erinnern uns:
Bei einer linearen Funktion (Gerade) waren es nur zwei Punkte.
Wenn wir den Graphen einer Parabel sauber zeichnen wollen, brauchen wir außer den vorgegebenen drei Punkten noch der Scheitelpunkt und die Achsenschnittpunkte .
Wenn wir zudem auch noch die Symmetrie zur Senkrechten durch den Scheitelpunkt berücksichtigen, benötigen wir in den meisten Fällen keine weiteren Punkte.
Parabel durch drei Punkte Interaktiv:
Wenn du in dem Javascript die Koordinaten der Punkte eingibst und danach auf Berechnen und anschließend auf Zeichnen klickst, kannst du deine Übungsaufgaben kontrollieren.
Funktionsgleichung einer Parabel mit weniger Angaben bestimmen
In einigen Fällen können wir die Funktionsgleichung mit weniger Angaben bestimmen.
Beispiel:
![]()
Bestimme die Funktionsgleichung f(x) und zeichne den Graphen.
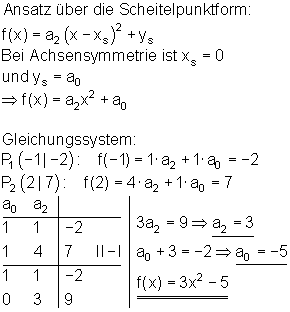
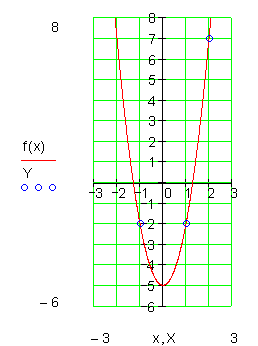
Beispiel:


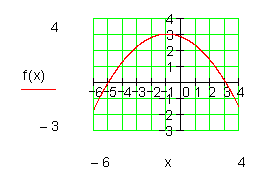
Aus der Angabe, dass der größte Funktionswert 3 ist, können wir schließen, dass die Parabel nach unten geöffnet ist. Das bestätigt auch die Rechnung.
Beispiel:
![]()
Bestimme den Funktionsterm und zeichne den Graphen.

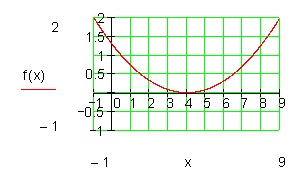
Beispiel:
Wenn man die Koordinaten der 3 vorgegebenen Punkte in die allgemeine Funktionsgleichung einsetzt, erhält man ein Gleichungssystem, bestehend aus 3 Gleichungen mit den drei Variablen a2 ; a1 und a0
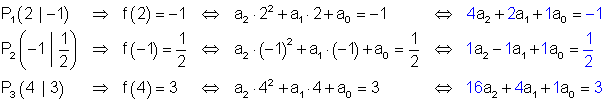
Lösung durch Additionsverfahren oder dem Gauß-Algorithmus.
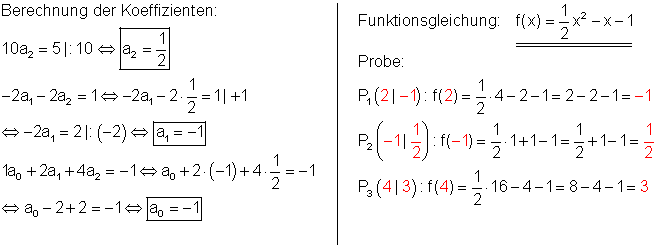
Berechnung der Achsenschnittpunkte.
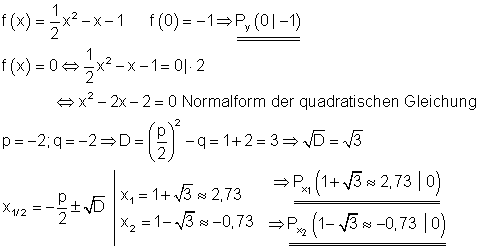
Der Scheitelpunkt: | 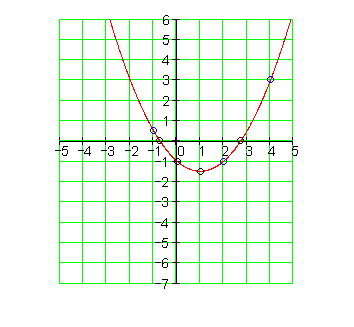 |
Anwendungsbeispiel für eine Parabel durch drei Punkte
Der parabelförmige Bogen einer Brücke mit der Spannweite 40 m hat eine maximale Höhe von 10 m.
Berechne die Längen der 7 in gleichen Abständen vertikal angebrachten Spannstäbe.
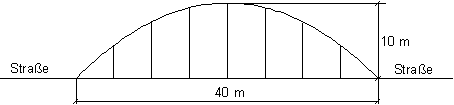
Modellierung:
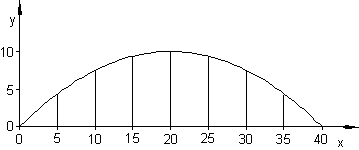
Wird das Koordinatensystem so gewählt, dann sind folgende Punkte bekannt:
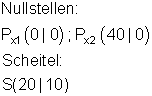
Lösung:
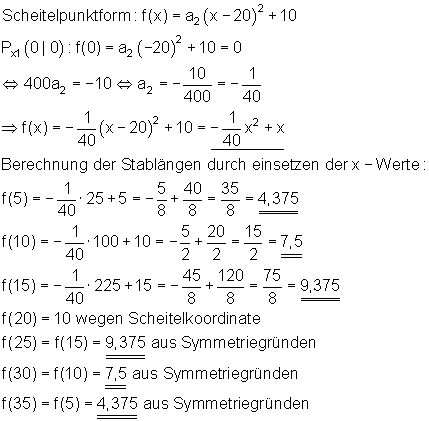
Dazu findest du hier eine Übersicht über alle Beiträge zum Thema Quadratische Funktionen, darin auch Links zu Aufgaben.


