Hier findet ihr die ausführlichen Lösungen zu den Aufgaben zur Integration der e-Funktion, uneigentliche Integrale und Berechnungen der Flächen.
1. Ausführliche Lösungen:
a)
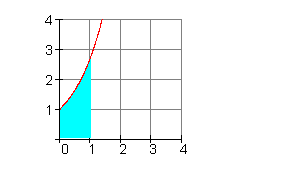
\int \limits_{0}^{1} e^x \,dx
= e^x \big\vert_{0}^{1} = e^1 - e^0 = e - 1 \approx 1,718
b)
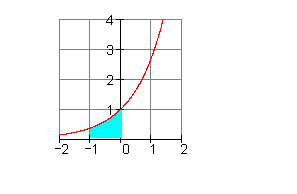
\int \limits_{-1}^{0} e^x \,dx
= e^x \big\vert_{-1}^{0} = e^0 - e^{-1} = 1 - e^{-1} \approx 0,632
c)
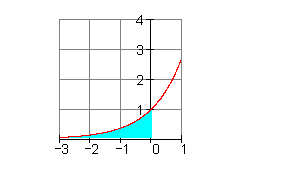
\int \limits_{-3}^{0} e^x \,dx
= e^x \big\vert_{-3}^{0} = e^0 - e^{-3} = 1 - e^{-3} \approx 0,950
2. Ausführliche Lösungen:
a)
\int \limits_{0}^{1} (e^x - 1) \,dx
= e^x - x \big\vert_{0}^{1} = e^1 - 1 - (e^0 - 0) = e - 1 - 1 \approx 0,718
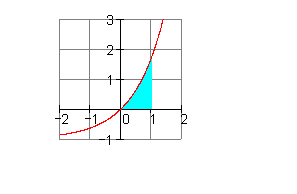
b)
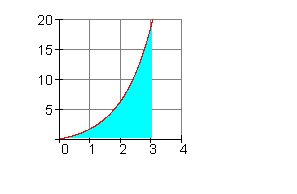
\int \limits_{0}^{3} (e^x - 1) \,dx
= e^x - x \big\vert_{0}^{3} = e^3 - 3 - (e^0 - 0) = e^3 - 3 - 1 \approx 16,086
c)
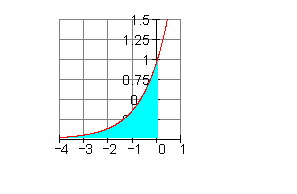
\int \limits_{-\infty}^{0} e^x \,dx = \lim \limits_{a\to\infty} \int \limits_{a}^{0} e^x \,dx
Zuerst berechnen wir ohne Grenzwertbildung:
\int \limits_{a}^{0} e^x \,dx = e^x \big\vert_{a}^{0} = e^0 - e^{a} = 1 - e^a
Als nächstes mit Grenzwertbildung:
\lim \limits_{a\to\infty} \int \limits_{a}^{0} e^x \,dx = \lim \limits_{a\to\infty} (1 - e^a) \\
= 1 - \underbrace{\lim \limits_{a\to\infty} e^a}_{0} = 1 \\
\Rightarrow \int \limits_{-\infty}^{0} e^x \,dx = 1
3. Ausführliche Lösungen:
a)
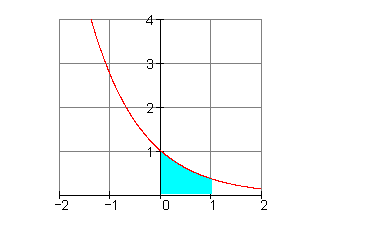
\int \limits_{0}^{1} e^{-x} \,dx Lösung durch Substitution
Substitution: u(x) = -x \\
\Rightarrow u'(x) = \frac{du}{dx} = - 1 \\
\Leftrightarrow dx = - du
Die untere Grenze ist folglich: u(0) = 0.
Die obere Grenze: u(1) = -1.
\Rightarrow -\int \limits_{0}^{-1} e^u \, du = \int \limits_{-1}^{0} e^u \, du = \\
e^u \big\vert_{-1}^{0} = e^0 - e^{-1} = 1 - e^{-1} \approx 0,632
b)
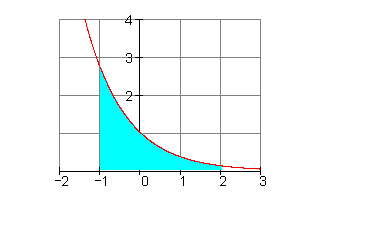
\int \limits_{-1}^{2} e^{-x} \,dx Lösung durch Substitution
Substitution: u(x) = -x \\
\Rightarrow u'(x) = \frac{du}{dx} = - 1 \\
\Leftrightarrow dx = - du
Die untere Grenze ist folglich: u(-1) = -(-1) = 1.
Die obere Grenze: u(2) = -2.
\Rightarrow -\int \limits_{1}^{-2} e^u \, du = \int \limits_{-2}^{1} e^u \, du = \\
e^u \big\vert_{-2}^{1} = e^1 - e^{-2} = e - e^{-2} \approx 2,583
c)
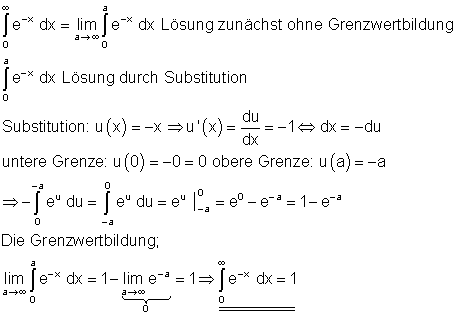
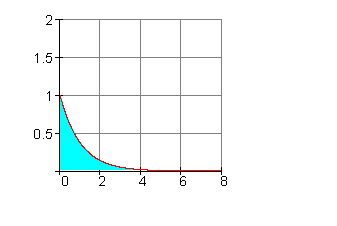
4. Ausführliche Lösungen:
a)

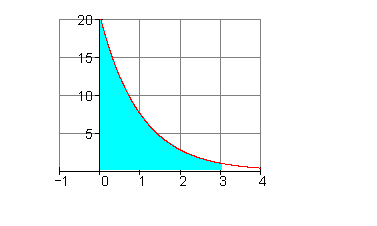
b)

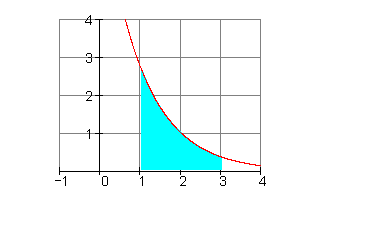
c)
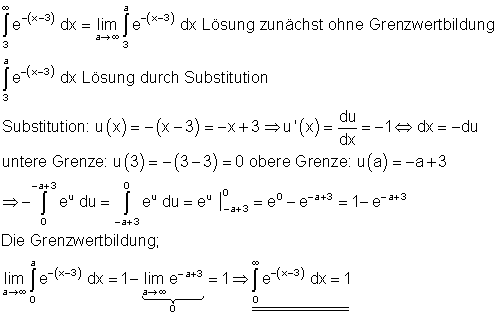
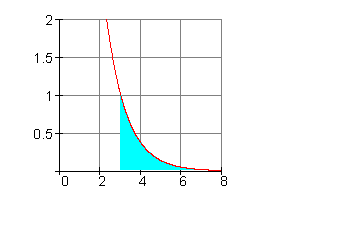
5. Ausführliche Lösungen:
a)
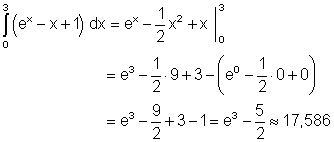
b)
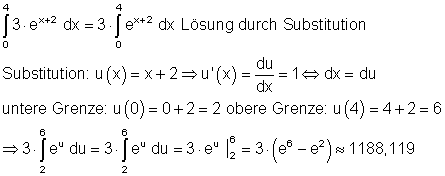
c)
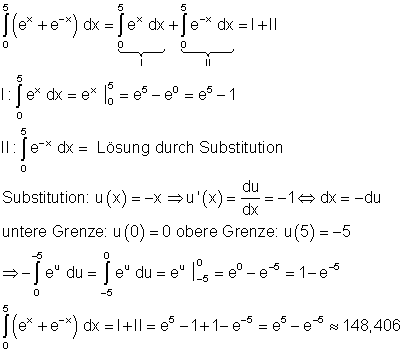
6. Ausführliche Lösungen:
a)
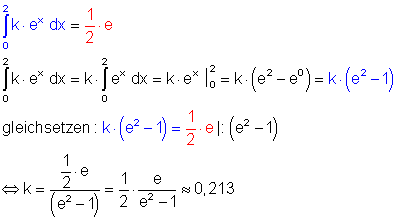
b)
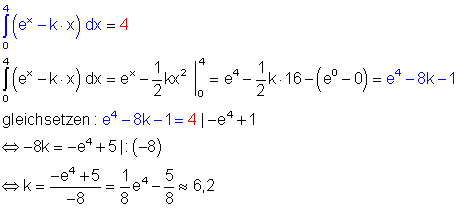
c)
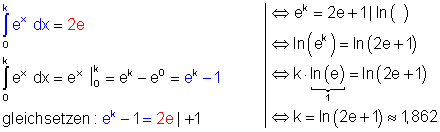
7. Ausführliche Lösungen:
a)
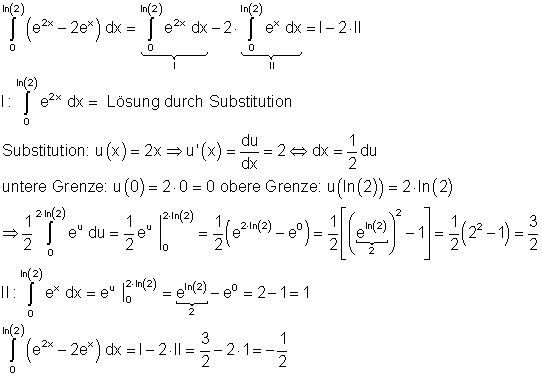
b)
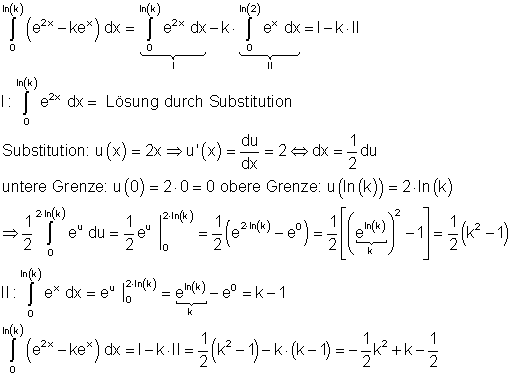
c)
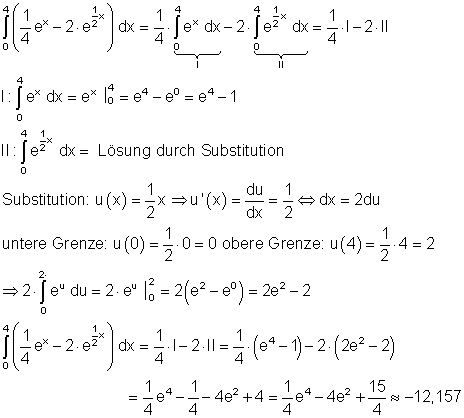
8. Ausführliche Lösungen:
a)
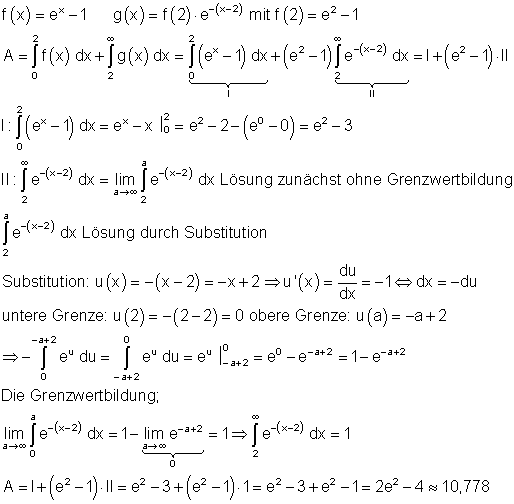
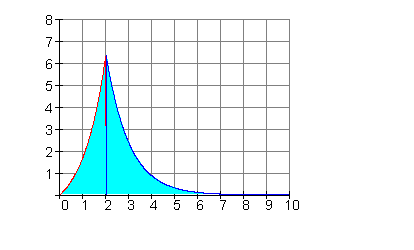
b)
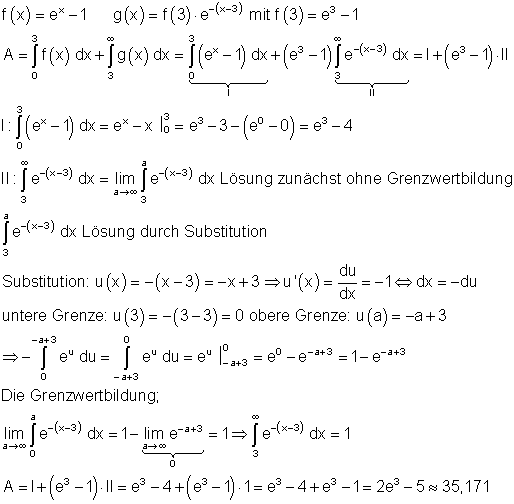
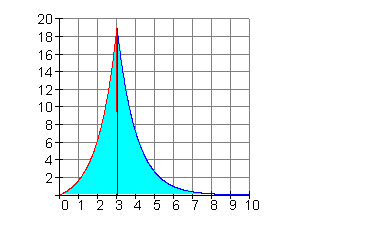
9. Ausführliche Lösungen:
a)
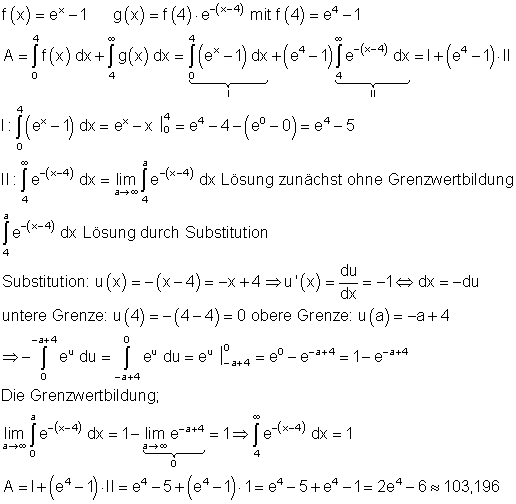
b)
Hier findest du die Aufgaben hierzu.
Und hier die Theorie hierzu: Integration der e-Funktion.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

